1/3/2023
1
TOÁN CAO CẤP
HỌC PHẦN II
TOÁN CAO CẤP HỌC PHẦN II
1
2
3
Giới hạn và liên tục của hàm số một biến số
Hàm số một biến số
Đạo hàm và vi phân của hàm số một biến số
4Tích phân
5Hàm số nhiều biến số và cực trị của hàm số
nhiều biến số
1/3/2023
2
CHƯƠNG 1
HÀM SỐ MỘT BIẾN SỐ
Cho 𝑿,𝒀⊆ℝ.
Hàm số 𝒇từ 𝑿vào 𝒀 là một quy tắc cho tương ứng mỗi phần tử 𝒙∈𝑿 với
một và chỉ một phần tử 𝒚∈𝒀. Kí hiệu:
𝒇:𝑿→𝒀
𝒙↦𝒚=𝒇(𝒙)
trong đó: 𝒙 là biến số, 𝒚là hàm số,
𝑿là miền xác định (hoặc tập xác định) của hàm số,
tập hợp 𝒇(𝒙):𝒙∈𝑿 là miền giá trị của hàm số.
Ví dụ 1:
Tìm miền xác định của các hàm số sau:
a) 𝒇𝒙 =𝟐𝒙−𝟏,b) 𝒇𝒙 = 𝒙𝟐−𝟏
,
c) 𝒇𝒙 =𝒍𝒐𝒈𝟐(𝟐−𝟑𝒙).
I. ĐỊNH NGHĨA HÀM SỐ
1/3/2023
3
1. Phép toán số học
Cho hai hàm số 𝒚=𝒇𝒙
,
𝒚=𝒈𝒙 với miền xác định 𝑫𝒇 và 𝑫𝒈khác rỗng.
Nếu 𝑫𝒇∩𝑫𝒈≠∅thì ta có các định nghĩa sau:
•Hàm tổng (tương ứng hàm hiệu):
𝒉𝒙 =𝒇𝒙+𝒈𝒙 (tương ứng 𝒉𝒙 =𝒇𝒙 −𝒈𝒙)với 𝒙∈𝑫𝒉=𝑫𝒇∩𝑫𝒈.
•Hàm tích:
𝒌𝒙 =𝒇𝒙𝒈𝒙 với 𝒙∈𝑫𝒌=𝑫𝒇∩𝑫𝒈.
•Hàm thương:
𝒑𝒙 =𝒇𝒙
𝒈𝒙 𝒗ớ𝒊 𝒙∈𝑫𝒑=𝑫𝒇∩𝑫𝒈\𝒙∈𝑫𝒈:𝒈𝒙 =𝟎.
(Tự đọc)
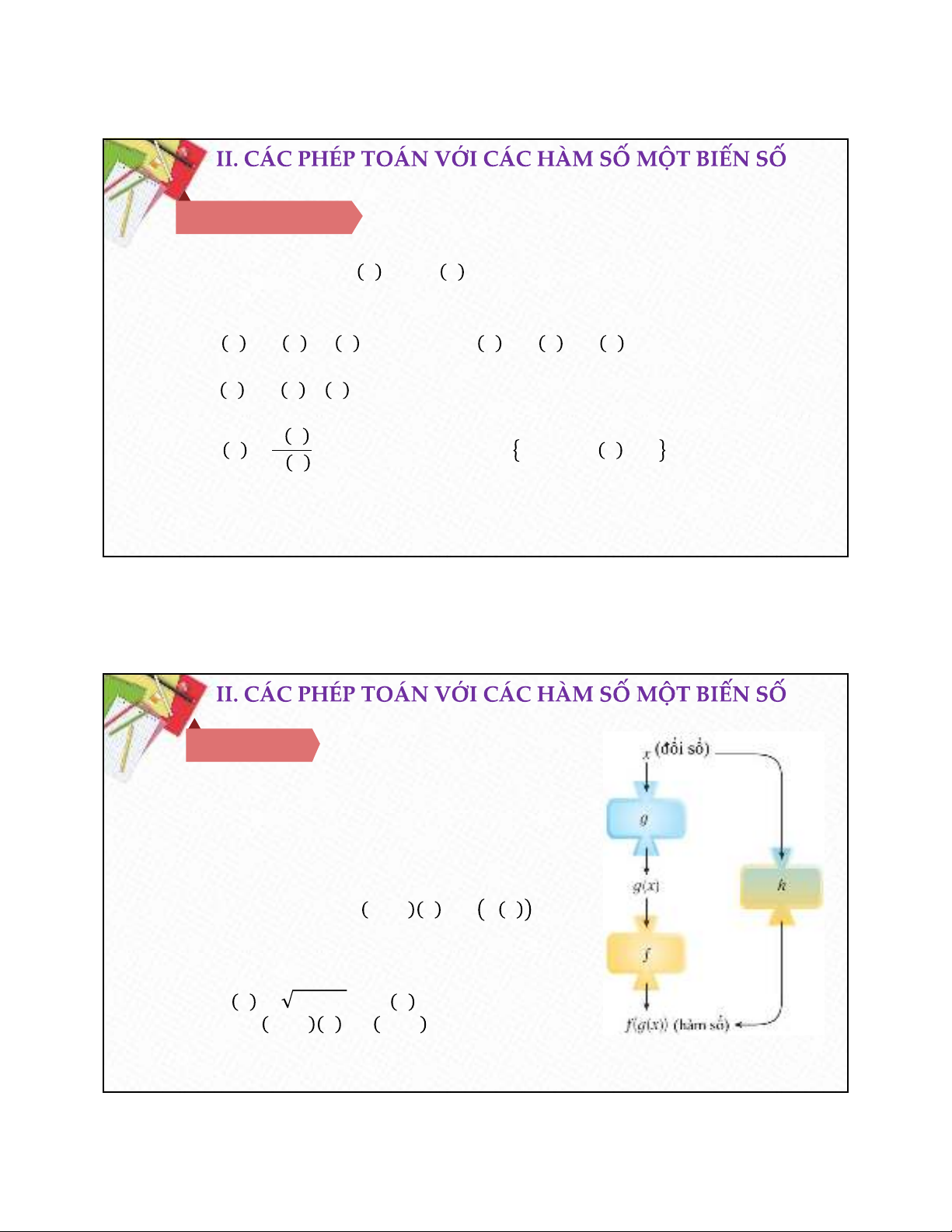
2. Hàm hợp.
Cho 𝑿,𝒀,𝒁⊆ℝ.
Cho hàm số 𝒈từ 𝑿vào 𝒀,hàm số 𝒇 từ 𝒀 vào 𝒁.
Hàm hợp của 𝒇với 𝒈được ký hiệu và xác
định như sau:
𝒇 ∘ 𝒈∶𝑿→𝒁
𝒙↦ 𝒇 ∘ 𝒈 𝒙 =𝒇𝒈𝒙
Ví dụ 2:
Cho 𝒇𝒙 = 𝟏−𝒙𝟐
và 𝒈𝒙 =𝒔𝒊𝒏𝒙.
Hãy tính 𝒇∘𝒈 𝒙 và 𝒈∘𝒇(𝒙).
(Tự đọc)
1/3/2023
4
3. Hàm ngược
Cho hàm số 𝒇:𝑿→𝒀
𝒙↦𝒚=𝒇(𝒙)
Hàm số 𝒇𝟏 từ 𝒀vào 𝑿được gọi là hàm
ngược của hàm số 𝒇 nếu thoả mãn:
𝒇𝟏 𝒇𝒙 =𝒙,∀𝒙∈𝑿.
Ví dụ 3:
(Tự đọc)
1. Hàm sơ cấp cơ bản
•Hàm hằng: 𝒚=𝒄,∀𝒙∈ℝ,𝒄là hằng số.
𝒚=𝒙𝜶,𝜶là số thực tuỳ ý.
•Hàm số luỹ thừa:
1/3/2023
5
1. Hàm sơ cấp cơ bản
•Hàm số mũ: 𝒚=𝒂𝒙,∀𝒙∈ℝ,𝟎<𝒂≠𝟏.
(i) 𝟎<𝒂<𝟏 (ii) 𝒂>𝟏
1. Hàm sơ cấp cơ bản
•Hàm số logarit: 𝒚=𝐥𝐨𝐠𝒂𝒙,∀𝒙>𝟎,𝟎<𝒂≠𝟏.
(i) 𝟎<𝒂<𝟏 (ii) 𝒂>𝟏
