CĐ TỰ LUẬN TOÁN 10 HÌNH HỌC_C1_VECTƠ
Fb: ThayTrongDgl Trang 1
CHƯƠNG 1
VECTƠ
BÀI 1. CÁC ĐỊNH NGHĨA
TÓM TẮT LÝ THUYẾT CƠ BẢN
1. Để xác định một véctơ cần biết một trong hai điều kiện sau:
- Điểm đầu và điểm cuối của vectơ.
- Độ dài và hướng.
2. Hai vectơ
a
và
b
được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
Nếu hai vectơ
a
và
b
cùng phương thì chúng có thể cùng hướng hoặc ngược hướng.
3. Độ dài của một vectơ là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó.
4.
=
ab
khi và chỉ khi
=
ab
và
a
,
b
cùng hướng.
5. Với mỗi điểm
A
ta gọi vectơ
AA
là vectơ-không. Vectơ-không được kí hiệu là
0
và quy ước rằng
00=
, vectơ
0
cùng phương cùng hướng với mọi vectơ.
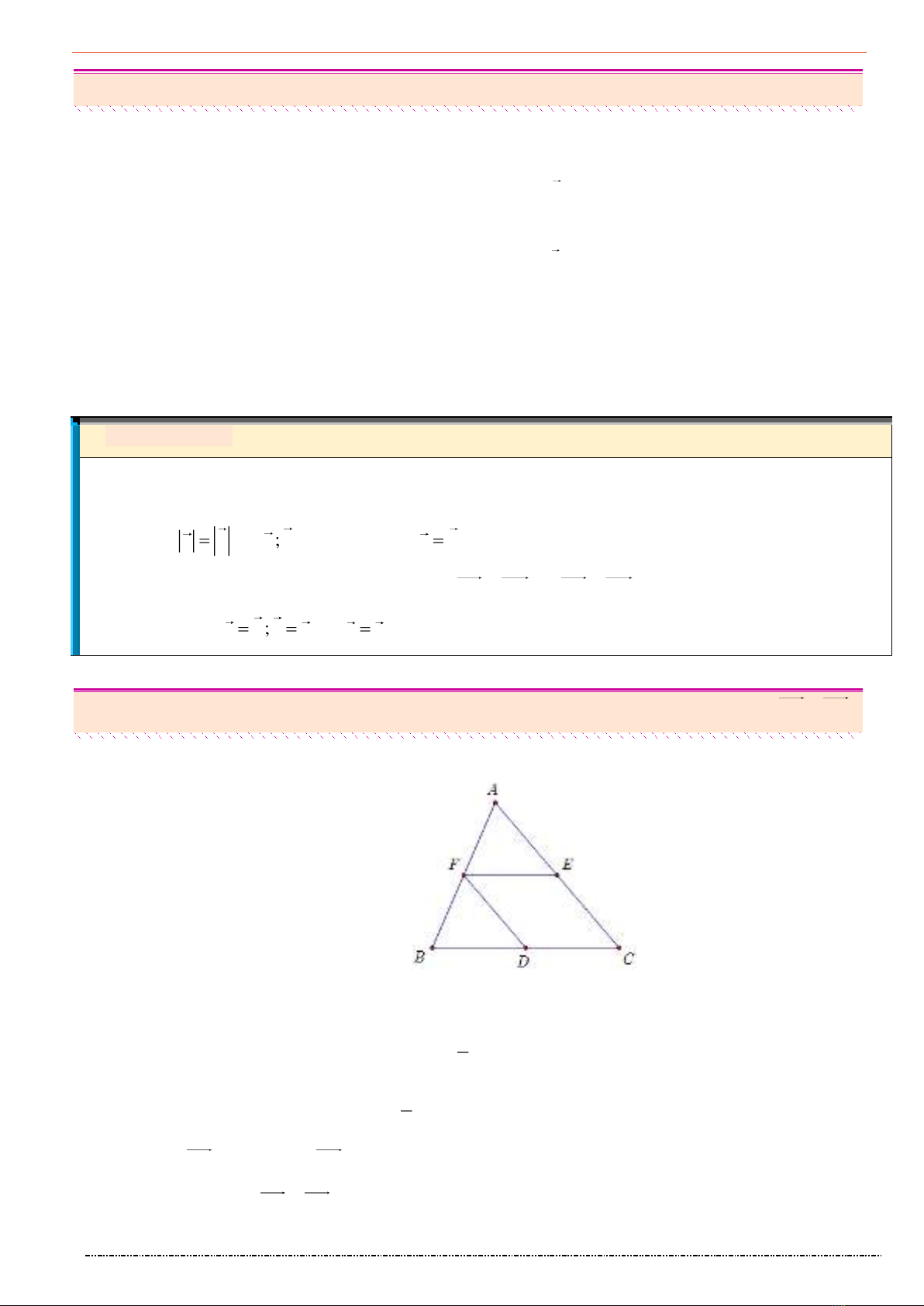
Bài 1. Cho 5 điểm phân biệt. Có bao nhiêu vectơ khác vectơ-không có điểm đầu và điểm cuối là các
điểm đã cho.
Lời gii
Xét các điểm
, , , ,A B C D E
phân biệt.
Các vectơ khác vectơ-không có điểm đầu và điểm cuối là các điểm trên là:
, , ,AB AC AD AE
,
, , ,BA BC BD BE
,
, , ,CA CB CD CE
,
, , ,DA DB DC DE
,
, , ,EA EB EC ED
.
Vậy có 20 véctơ khác vectơ-không có điểm đầu và điểm cuối là các điểm đã cho.
Bài 2. Cho Hãy tính số các vectơ mà các điểm đầu và điểm cuối được lấy từ các điểm phân biệt đã cho
DẠNG TOÁN 1: XÁC ĐỊNH MỘT VECTƠ, SỰ CÙNG PHƯƠNG VÀ HƯỚNG CỦA HAI
VECTƠ.
PHƯƠNG PHÁP
• Để xác định vectơ ta cần biết điểm đầu và điểm cuối của vectơ hoặc biết độ dài và hướng của chúng.
Chẳng hạn với hai điểm
,AB
phân biệt, ta có hai vectơ khác vectơ-không là
AB
và
BA
.
• Vectơ
a
là vectơ-không khi và chỉ khi
0=
a
hoặc
=
a AA
với
A
là điểm bất kì.