Bài giảng Công nghệ Xử lý Ảnh Số Mai Cường Thọ phần 1

Bài giảng Xử lý ảnh số

GV. Mai Cường Thọ

Lời mở đầu

Xử lý ảnh là một ngành khoa học còn tương đối mới mẻ so với nhiều ngành khoa

học khác. Hiện nay nó đang là một trong những lĩnh lực được quan tâm và đã trở

thành môn học chuyên ngành của sinh viên hệ kỹ sư, cử nhân ngành Công nghệ

Thông tin.

Nhờ có công nghệ số hóa hiện đại, ngày nay con người đã có thể xử lý tín hiệu

nhiều chiều thông qua nhiều hệ thống khác nhau, từ những mạch số đơn giản cho

đến những máy tính song song cao cấp. Mục tiêu của xử lý này có thể chia làm ba

hướng như sau:

Xử lý ảnh ban đầu để có được ảnh mới theo một yêu cầu xác định (ví dụ như

ảnh mờ cần xử lý để được ảnh rõ hơn)

Phân tích ảnh để thu được các thông tin đặc trưng giúp cho việc phân loại,

nhận biết ảnh (ví dụ phân tích ảnh vân tay để trích chọn các đặc trưng vân

tay)

Hiểu ảnh đầu vào để có những mô tả về ảnh ở mức cao hơn, sâu hơn (ví dụ từ

ảnh mộttai nạn giao thông phác họa hiện trường tai nạn).

Trong bài giảng này, chúng ta sẽ tập trung vào những khái niệm cơ bản của xử lý

ảnh và giới hạn vấn đề trong phạm vi 2 – chiều

Các ứng dụng trong:

- Sản xuất và kiểm tra chất lượng

- Di chuyển của Robot

- Các phương tiện đi lại tự trị

- Công cụ hướng dẫn cho người mù

- An ninh và giám sát

- Nhận dạng đối tượng, nhận dạng mặt

- Ứng dụng trong y học

- Sản xuất, hiệu chỉnh Video

- Chinh phục vũ trụ…

Với những ứng dụng to lớn của công nghệ xử lý ảnh, chúng ta hãy bắt tay vào

ngay từ bây giờ tìm hiểu, làm việc với một trong những thế giới đầy tiềm năng này.

Bài giảng Xử lý ảnh số

GV. Mai Cường Thọ

Chương I

Tổng quan về hệ thống xử lý ảnh và các vấn đề trong xử lý ảnh

I. Ảnh và Hệ thống xử lý ảnh

1. Ảnh

- Tín hiệu ảnh thuộc loại tín hiệu đa chiều: tọa độ(x,y,z), độ sáng(λ), thời gian(t).

- Ảnh tĩnh trong không gian 2 chiều được định nghĩa là một hàm 2 biến S(x,y), với S

là giá trị biên độ (được biểu diễn bằng màu sắc) tại vị trí không gian (x,y).

- Phân loại ảnh

+ Ảnh tương tự S(x,y): (x,y) liên tục, S liên tục.

+ Ảnh số S(m,n): (m,n) rời rạc, S rời rạc.

- Một ảnh (gồm một tập các điểm ảnh) có thể xem như bao gồm tập các ảnh con (các

vùng ảnh). Thuật ngữ gọi là ROIs – vùng quan tâm (Regions of Interest).

- Ảnh số trong không gian rời rạc thu được từ ảnh tương tự trong không gian liên tục

thông qua quá trình số hóa. Quá trình số hóa có thể hiểu đơn giản như sau

+ Ảnh tương tự được chia thành M hàng, N cột.

+ Giao của hàng và cột được gọi là: pixel

+ Giá trị biên độ của pixel tại tọa độ nguyên (m,n) là s(m,n): là trung bình độ

sáng trong pixel đó.

LnmS

≤

),(

(L số mức xám dùng biểu diễn ảnh).

- M, N thường được chọn là M=N=2

(K=8,9,10). L =2

, B là số bít mã hóa cho độ

sáng(biên độ) mỗi pixel.

- Ảnh số được biểu diễn bởi ma trận 2 chiều. Các phần tử của nó là biểu diễn cho

các pixel số hóa.

- Ta ký hiệu 1 ảnh số là S(M,N). Ta nói ảnh có độ phân giải MxN. Ký hiệu s(m,n) để

chỉ ra một phần tử ảnh.

Hình 1.1 : Ảnh tương tự và Ảnh số hóa

Bài giảng Xử lý ảnh số

GV. Mai Cường Thọ

2. Hệ thống xử lý ảnh

- Xử lý ảnh: Ảnh vào → Ảnh kết quả.

- Đối tượng xử lý của hệ thống ở đây là các ảnh (hàm 2 biến liên tục hoặc rời rạc).

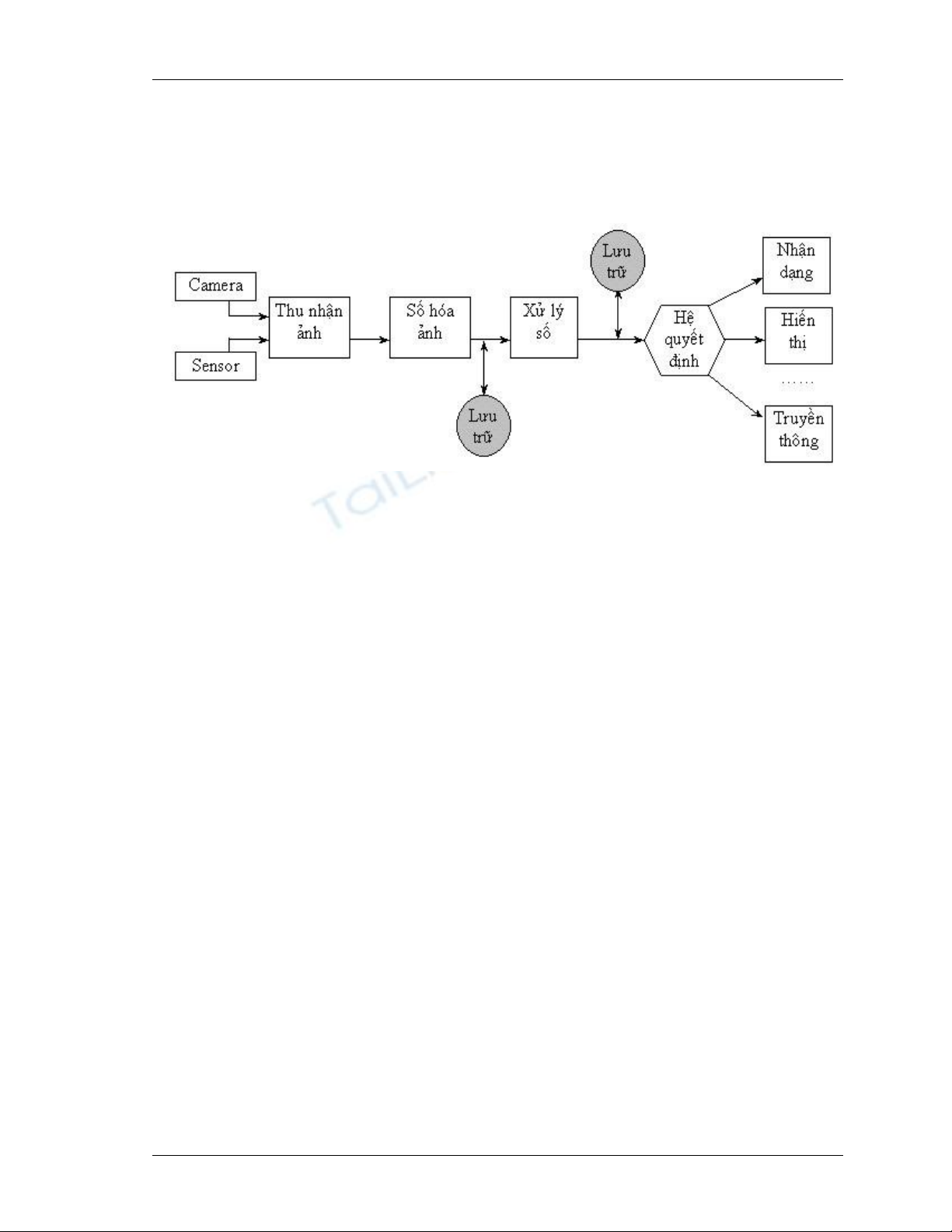
- Có thể tóm tắt hệ thống xử lý ảnh gồm các giai đoạn chính như sau:

Hình 1.2 Các giai đoạn chính trong hệ thống xử lý ảnh

+ Thu nhận ảnh: - Qua các camera (tương tự, số).

- Từ vệ tinh qua các bộ cảm ứng (Sensors).

- Qua các máy quét ảnh (Scaners).

+ Số hóa ảnh: Biến đổi ảnh tương tự thành ảnh rời rạc để xử lý bằng máy tính:

Thông qua quá trình lấy mẫu (rời rạc về mặt không gian) và lượng tử hóa (rời rạc về

mặt biên độ).

+ Xử lý số: là một tiến trình gồm nhiều công đoạn nhỏ: Tăng cường ảnh

(Enhancement), khôi phục ảnh (Restoration), phát hiện biên (Egde Detection), phân

vùng ảnh (Segmentation), trích chọn các đặc tính (Feature Extraction)...

+ Hệ quyết định: Tùy mục đích của ứng dụng mà chuyển sang giai đoạn khác là

hiển thị, nhận dạng, phân lớp, truyền thông…

II. Các vấn đề cơ bản trong xử lý ảnh

1. Biểu diễn và mô hình hóa ảnh

 Biểu diễn ảnh

- Ảnh có thể xem là một hàm 2 biến chứa các thông tin như biểu diễn của một ảnh.

Các mô hình biểu diễn ảnh cho ta một mô tả logic hay định lượng của hàm này. Dựa

vào phần tử đặc trưng của ảnh đó là pixel. Giá trị pixel có thể là một giá trị vô

hướng, hoặc là 1 vector (3 thành phần trong trường hợp ảnh màu).

- Ta có thể biểu diễn ảnh bằng hàm toán học, hoặc các ma trận điểm. Trong mô

hình toán học, ảnh hai chiều được biểu diễn nhờ các hàm hai biến, đó là

Bài giảng Xử lý ảnh số

GV. Mai Cường Thọ

∑ ∑

∞

−∞=

∞

−∞=

−−=

k l

lnkmlkSnmS ),(),(),( δ

với

1,0,1,0 −≤≤−≤≤ NlnMkm

 Biểu diễn bằng hàm toán

- S: ảnh

- (m,n): Tọa độ của Pixel trong miền không gian (2D)

- s(m,n): Độ sáng (Mức xám) của pixel (m,n).

- [0-L

max

]: Thang mức xám - Vùng các mức xám được phép sử dụng. L

max

thường

là 255, nghĩa là chúng ta sử dụng thang mức xám 8 bit.

255),(0

≤

nms

- Với

10,10 −≤≤−≤≤ NnMm

, ta gọi đó là ảnh số M x N

 Biểu diễn bằng ma trận điểm:

Hình 1.3 a, Ảnh thật 10x10; b, Ảnh được zoom; c, Mô tả ảnh bằng ma trận điểm

 Mô hình hóa ảnh

- Mô hình cảm nhận ảnh: Là mô hình biểu diễn thông qua các thuộc tính cảm nhận

ảnh (màu sắc, cường độ sáng), các thuộc tính về thời gian, các cảm nhận về phối

cảnh, bố cục.

- Mô hình cục bộ: Là mô hình biểu diễn thể hiện mối tương quan cục bộ của các

phần tử ảnh (ứng dụng cho các bài toán xử lý và nâng cao chất lượng ảnh).

- Mô hính tổng thể: Là mô hình biểu diễn ảnh xem ảnh như là một tập hợp các đối

tượng, và các đối tượng này có mối quan hệ không gian với nhau (ứng dụng cho các

bài toán phân nhóm và nhận dạng ảnh).

2. Tăng cường ảnh

 Mục đích: Tăng cường các thuộc tính cảm nhận, làm cho ảnh tốt lên theo một ý

nghĩa nào đó, tiện phục vụ cho các xử lý tiếp theo.

Bài giảng Xử lý ảnh số

GV. Mai Cường Thọ

 Các thao tác:

- Thay đổi độ tương phản, thay đổi màu sắc, cường độ sáng, lọc nhiễu, nội suy, làm

trơn ảnh.

 Các phương pháp chính:

- Các phương pháp thao tác trên điểm (Point Operation)

- Các thao tác không gian (Spatial Operation)

3. Khôi phục ảnh

 Mục đích: Khôi phục lại ảnh ban đầu, loại bỏ các biến dạng ra khỏi ảnh tùy theo

nguyên nhân gây ra biến dạng.

∫ ∫

∞

∞−

∞

∞−

+= )),((),(),;,(),( yxddfyxhyxg ηβαβαβα

),( yx

là hàm biểu diễn nhiễu cộng.

),(

là hàm biểu diễn đối tượng.

),( yxg

là ảnh thu nhận.

),;,(

yxh

là đáp ứng xung của hệ thống, còn gọi là hàm tán xạ điểm (Point Spread

Function- PSF).

Một vấn đề khôi phục ảnh tiêu biểu là tìm một xấp xỉ của

),(

khi PSF có thể

đo lường hay quan sát được, ảnh mờ và các tính chất sác xuất của quá trình nhiễu.

 Các thao tác: lọc nhiễu, giảm độ méo,…

 Các phương pháp: lọc ngược, lọc thích nghi (Wiener), khôi phục ảnh từ các hình

chiếu.

4. Biến đổi ảnh

 Mục đích: Biến đổi thể hiện của ảnh dưới các góc nhìn khác nhau tiến cho việc xử

lý, phân tích ảnh.

 Các phương pháp: Biến đổi Fourier, Sin, Cosin, KL, …

5. Phân tích ảnh

 Mục đích: Tìm ra các đặc trưng của ảnh, xây dựng quan hệ giữa chúng dựa vào

các đặc trưng cục bộ.

 Các thao tác: Tìm biên, tách biên, làm mảnh đường biên, phân vùng ảnh, phân

loại đối tượng.

ệ

ố

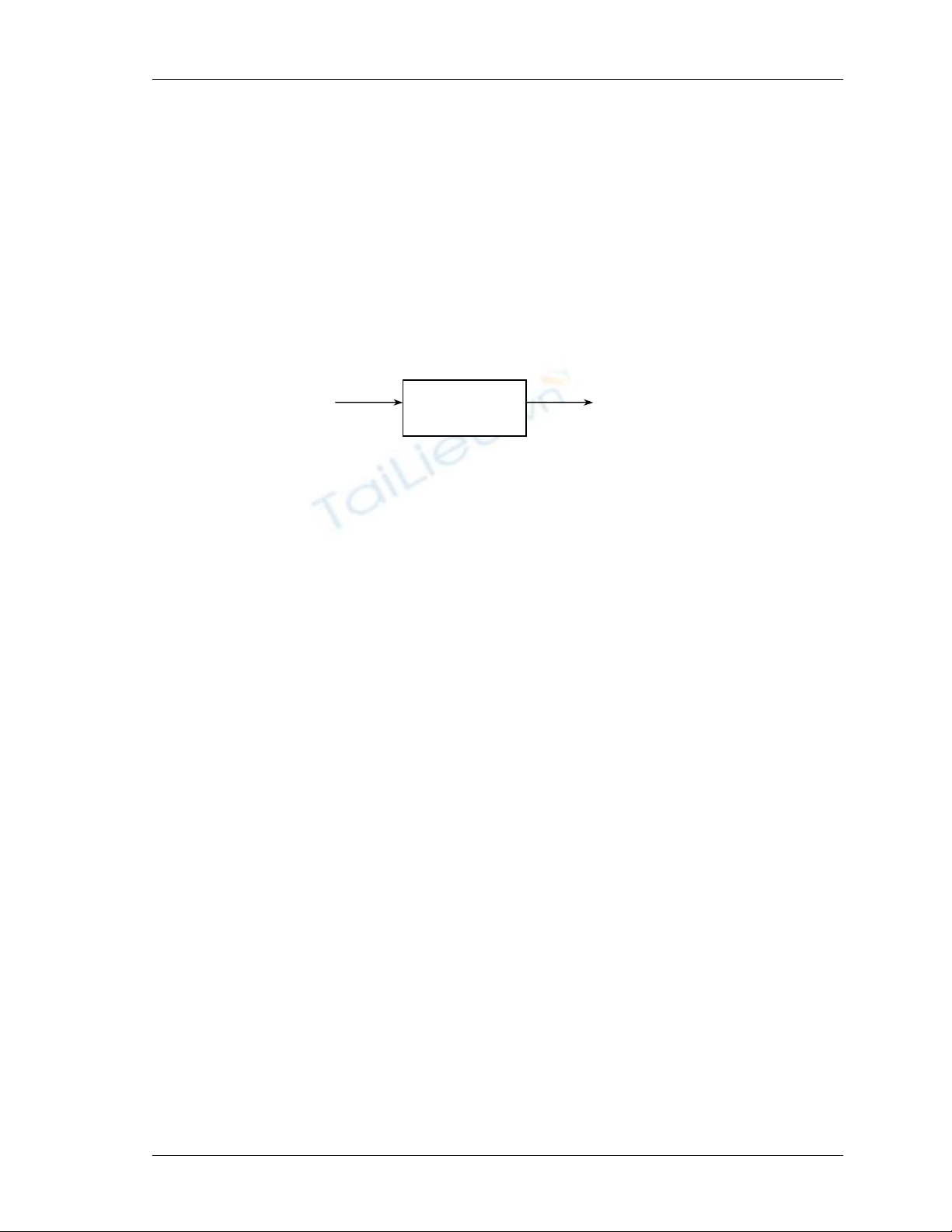
ng thu

ậ

ả

Ả

đầ

u ra

),( yxg

Ả

đầ

u vào

),(

),;,(

yxh

Bài Giảng Công Nghệ Xử Liý Ảnh Số - Mai Cường Thọ phần 1

Chủ đề:

Tài liệu liên quan

Tài liêu mới

AI tóm tắt

Giới thiệu tài liệu

Đối tượng sử dụng

Từ khoá chính

Nội dung tóm tắt

Hỗ trợ

Phương thức thanh toán

Theo dõi chúng tôi