
(c) SE/FIT/HUT 2002 1
Bài 5
Nguyên lý về3D và
Phép chiếu-Projection
Lê Tấn Hùng
0913030731
hunglt@it-hut.edu.vn
(c) SE/FIT/HUT 2002 2
Nguyên lý về3D
Ðồhọa3 chiều - 3D computer graphics bao gồmviệcbổ
xungkíchthướcvềchiềusâucủađốitượng, cho phép ta biểu
diễn chúng trong thếgiớithựcmột cách chính xác và sinh
động hơn.
Tuy nhiên các thiếtbịtruy xuấthiệntạiđềulà2 chiều, Do
vậyviệcbiểudiễnđượcthực thi thông qua phép tô chát –
render để gây ảo giác illusion vềđộsâu
3D Graphics là việcchyểnthếgiớitựnhiên dướidạng các mô
hình biểudiễn trên các thiếtbịhiểnthịthông qua kỹthuậttô
chát (rendering).
(c) SE/FIT/HUT 2002 3
Ðặcđiểmcủakỹthuậtđồ hoạ3D
Có các đốitượng phứctapjhơn các đốitượng trong
không gian 2D
Bao bởi các mặtphẳng hay các bềmặt
Có các thành phần trong và ngoài
Các phép biếnđổihìnhhọcphứctạp
Các phép biếnđổihệtoạđộphứctạphơn
Thường xuyên phảibổxung thêm phép chiếutừ
không gian 3D vào không gian 2D
Luôn phảixácđịnh các bềmặthiểnthị
(c) SE/FIT/HUT 2002 4
Các phương pháp hiểnthị3D
Vớicácthiếtbịhiểnthị2D:
3D viewing positions
Kỹthuậtchiếu - projection: orthographic/perspective
Kỹthuậtđánh dấuđộ sâu - depth cueing
Nét khuất - visible line/surface identification
Tô chát bềmặt-surface rendering
Cắt lát - exploded/cutaway scenes, cross-sections
Thiếtbịhiểnthị3D:
Kính stereo - Stereoscopic displays*
Màn hình 3D - Holograms
(c) SE/FIT/HUT 2002 5
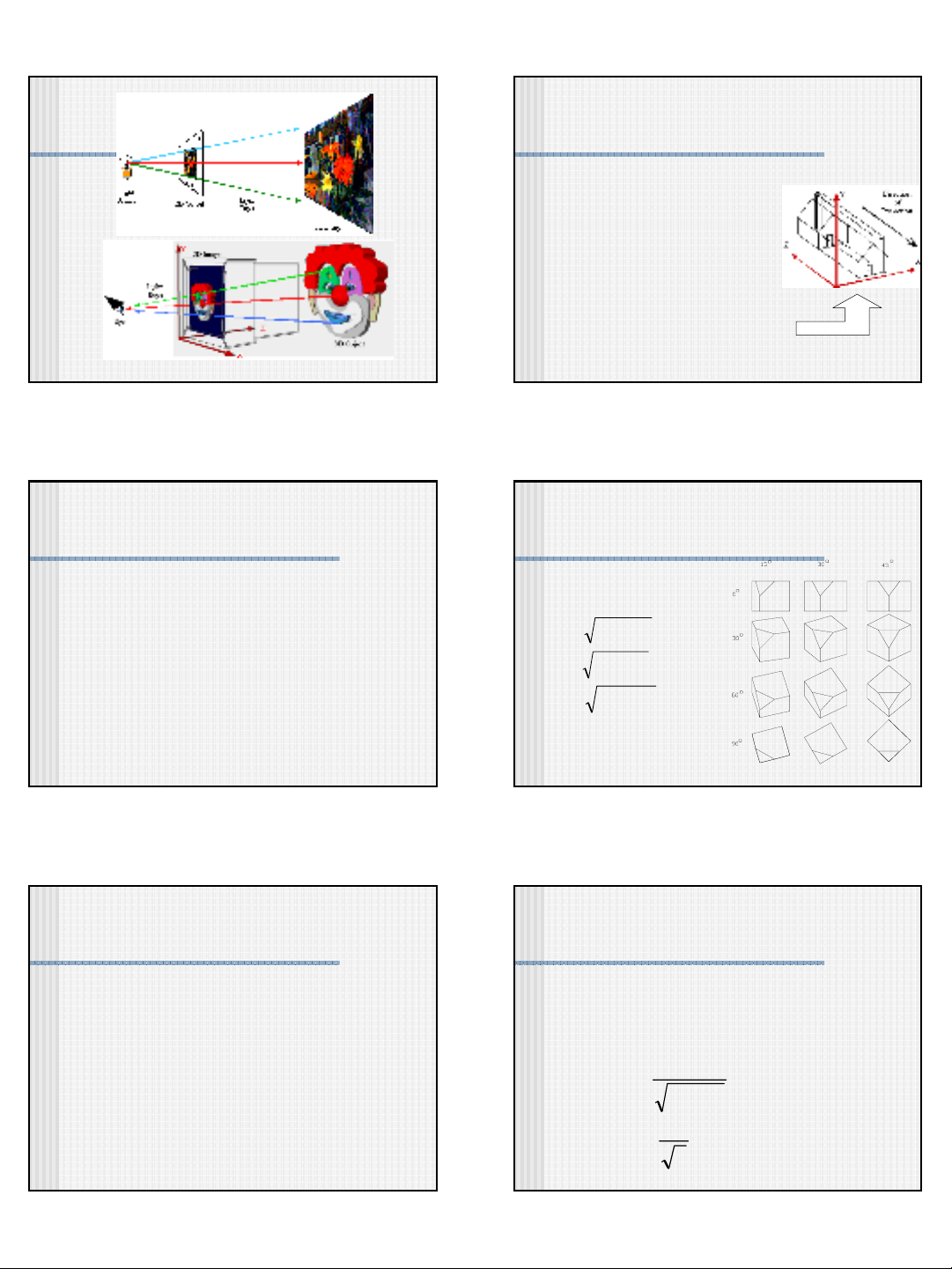
Different views of a 3D model
Shadows as depth cues
Perspective and
Depth of Field
Exploded/cutaway scenes
(c) SE/FIT/HUT 2002 6
3D GRAPHICS PIPELINE
WORLD SCENE/OBJECT
3D MODELLING
3D CLIPPING
PROJECTION
RASTERIZATION
2D PIXELMAP DISPLAY
Modelling coordinates:
- world coordinate system,
- object coordinate system
Camera coordinates
Screen/Window coordinates
Device coordinates
VIEWING

(c) SE/FIT/HUT 2002 7
3D - Modelling
3D Modelling
Parametric
Polygonal
Particles
Implicit
2222 rzyx =++
θ
θ
2
4
cos
sin
=
=
y
x
(c) SE/FIT/HUT 2002 8
Clipping 3D
view frustrum
outside view so
must be clipped
(c) SE/FIT/HUT 2002 9
Viewing and Projection
viewport
3d models
camera setup
(c) SE/FIT/HUT 2002 10
Rasterization
(c) SE/FIT/HUT 2002 11
Phép chiếu
Định nghĩavềphép chiếu
Định nghĩavềhình chiếu
Ảnh củađốitượng trên mặtphẳng chiếuđược hình thành từ
phép chiếubởi các đường thẳng gọi là tia chiếu(projector)
xuất phát từmộtđiểmgọilàtâmchiếu(center of projection)
đi qua các điểmcủađốitượng giao vớimặtchiếu(projection
plan).
(c) SE/FIT/HUT 2002 12
Các bướcxâydựng hình chiếu
1. đốitượng trong không gian 3Dvớitọađộ thựcđượccắttheomột không gian
xác định gọilàviewvolume.
2. view volume đượcchiếulênmặtphẳng chiếu. Diện tích choán bởiviewvolume
trên mặtphẳng chiếuđósẽcho chúng ta khung nhìn.
3. là việcánhxạkhung nhìn vào trong mộtcổng nhìn bấtkỳcho trướctrênmàn
hình để hiểnthịhình ảnh
C¾t theo view
volum PhÐp chiÕu trªn
mÆt ph¼ng chiÕu
PhÐp biÕn ®æi vµo
cæng nh×n cña
täa ®é thiÕt bÞ
täa ®é thùc
3D täa ®é theo vïng
c¾t khung nh×n täa ®é thiÕt
bÞ
(c) SE/FIT/HUT 2002 13 (c) SE/FIT/HUT 2002 14
Phép chiếu song song
Parallel Projections
Phép chiếu song song - Parallel Projections
Phân loạiphépchiếusong songdựatrênhướng của tia
chiếuDirection Of Projection và mặtphẳng chiếu-
projection plane
Phép chiếutrực giao (Orthographic projection)
Ứng vớimỗimặtphẳng chiếutacó1 ma trậnchiếu
tương ứng
=
1000
0000
0010
0001
][ z
T
=
1000
0100
0000
0001
][ y
T
=
1000
0100
0010
0000
][ x
T
(c) SE/FIT/HUT 2002 15
Phép chiếutrụclượng (Axonometric)
Phép chiếutrụclượng
Phép chiếu Trimetric
trên cơsởtỉlệco -SF củaảnh đốitượng trên mỗitrụclà
khác nhau.
=
=
1000
10
10
10
][
1100
1010
1001
][ ''
''
''
zz
yy
xx
yx
yx
yx
TU
(c) SE/FIT/HUT 2002 16
Trimetric
SF-tỉlệco theo các trụclà:
2
x
2
xx 'y'xf +=
2
y
2
yy 'y'xf +=
2
z
2
zz 'y'xf +=
(c) SE/FIT/HUT 2002 17
Phép chiếuDimetric
]][][[][ PzRxRyT =
−
−
=
1000
0000
0010
0001
1000
00
00
0001
1000
00
0010
00
.
cossin
sincos
.
cossin
sincos
ϕϕ
ϕϕ
φφ
φφ
−
=
1000
00sincossin
00cos0
00sinsincos
][
ϕφφ
ϕ
ϕφφ
T
Là phép chiếu Trimetric với2 hệ
sốtỉlệco bằng nhau, giá trịthứ3
còn lạilàtuỳý.
(c) SE/FIT/HUT 2002 18
ϕ
2222 cos)( '' =+= yyy yxf
ϕφφ
222222 sincossin)( '' +=+= zzz yxf
)(sin
2
1z
f
±= −
ϕ
)(sin
2
1
2z
z
f
f
−
±= −
φ

(c) SE/FIT/HUT 2002 19
Phép chiếu Isometric
ϕ
ϕ
φ
2
2
2
1sin
sin
sin −
=
ϕ
ϕ
φ
2
2
2
1
21
sin
sin
sin −
−
=
3
1
±=
ϕ
sin
0
45
0
26.35
±= ±=
φ
ϕ
21
311
31
12
2
2/
/
/
sin
sin
sin =
−
=
−
=
ϕ
ϕ
φ
8165.03/2cos2===
ϕ
f
(c) SE/FIT/HUT 2002 20
.
(c) SE/FIT/HUT 2002 21
Parallel Projections
axonometric
orthographic
oblique
isometric (c) SE/FIT/HUT 2002 22
Phép chiếuxiên-Oblique
Phép chiếu Cavalier
Phép chiếu Cabinet
(c) SE/FIT/HUT 2002 23
Phép chiếu Cavalier
−−
=
1000
00
0010
0001
]''[ ba
T
α
α
sinfb
f
=
=
cos a
−−
=
1000
00sincos
0010
0001
][
αα
ff
T
(c) SE/FIT/HUT 2002 24
f = 0, β= 900phép chiếu
sẽtrởthành phép chiếu
trựcgiao.
Còn với f = 1 kích thước
củahìnhchiếubằng kích
thướccủađốitượng =>
cavalier
Phép chiếu Cavalier cho
phép giá trịcủaαbiến
đổimột cách tựdo α=
300và 450

(c) SE/FIT/HUT 2002 25
Phép chiếuCabinet
Phép chiếuxiênvớihệsốco tỉlệf = 1/2
0
22
1
22
1
435.63)
)21(1
2
1
(cos
)
1
(cos
=
+
=
+
=
−
−
f
f
β
(c) SE/FIT/HUT 2002 26
Oblique Projections
D/2
D
D
D
Cavalier Project
Cabinet Projection
(c) SE/FIT/HUT 2002 27
Phép chiếuphốicảnh
Perspective Projection
Phép chiếuphốicảnh
Các đoạnthẳng song song củamôhình3D sauphépchiếuhộitụtại1 điểmgọilà
điểmtriệt tiêu - vanishing point
Phân loại phép chiếuphốicảnh dựavàotâmchiếu-Centre Of Projection (COP) và
mặtphẳng chiếu projection plane
(c) SE/FIT/HUT 2002 28
Vanishing points
Each set of parallel lines (=direction) meets at a different
point: The vanishing point for this direction
Sets of parallel lines on the same plane lead to collinear
vanishing points: the horizon for that plane
Easy examples
corridor
higher = further away
Good way to spot faked images
(c) SE/FIT/HUT 2002 29
Điểm triệt tiêu
Vanishing point
điểm triệt tiêu quy tắc - principle vanishing point
The number of principal vanishing points is determined by
the number of principal axes cut by the projection plane.
If the plane only cut the z axis (most common), there is only
1 vanishing point.
2-points sometimes used in architecture and engineering. 3-
points seldom used … add little extra realism
(c) SE/FIT/HUT 2002 30
Perspective Projections
3-point perspective
2-point perspective
1-point perspective




![Bài giảng Đồ hoạ kỹ thuật 1: Phần 1 - Trường ĐH Thuỷ Lợi [Mới Nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2023/20230131/baphap06/135x160/672431589.jpg)


![Bài giảng Lập trình trực quan: Tổng hợp kiến thức [Năm]](https://cdn.tailieu.vn/images/document/thumbnail/2022/20221025/minhtam37847/135x160/684443159.jpg)


















