21/01/2015
1
CHỈ SỐ
KHÁI NIỆM
Chỉ số là gì?
là một loại số tương đối đặc biệt nhằm nghiên cứu
biến động của các hiện tượng kinh tế xã hội phức tạp
chịu ảnh hưởng của nhiều nhân tố có mối quan hệ tích
số
2
PHÂN LOẠI
3
Căn cứ vào phạm vi tính toán
Chỉ số cá thể: là những chỉ số biểu hiện biến động của
từng phần tử, từng đơn vị cá biệt trong tổng thể nghiên
cứu
Chỉ số tổng hợp: biểu hiện biến động của tất cả các đơn
vị, các phần tử của tổng thể nghiên cứu.
PHÂN LOẠI
4
Căn cứ vào tính chất của chỉ tiêu thống kê:
Chỉ số của chỉ tiêu khối lượng: là chỉ số biểu hiện sự biến
động của các chỉ tiêu khối lượng.
Chỉ số của chỉ tiêu chất lượng: biểu hiện biến động của
các chỉ tiêu chất lượng.
21/01/2015
2
5
PHÂN LOẠI
Căn cứ vào tác dụng của chỉ số:
Chỉ số phát triển: biểu hiện biến động của hiện tưượng
qua thời gian
Chỉ số không gian: biểu hiện sự biến động của hiện
tưượng qua những không gian khác nhau.
Chỉ số kế hoạch: biểu hiện các nhiệm vụ kế hoạch hay
tình hình thực hiện
Chỉ số thời vụ: biểu hiện tính chất và mức biến động thời
vụ.
MOÄT SOÁ KYÙ HIEÄU THÖÔØNG SÖÛ DUÏNG:
p : GIAÙ CAÛ
q : KHOÁI LÖÔÏNG SAÛN PHAÅM
Z : GIAÙ THAØNH
W: NAÊNG SUAÁT LAO ÑOÄNG
0 : KYØ GOÁC
1: KYØ BAÙO CAÙO
T : LÖÔÏNG LAO ÑOÄNG
D : DIEÄN TÍCH TROÀNG TROÏT
N : NAÊNG SUAÁT THU HOAÏCH
L : TIEÀN LÖÔNG
6
CHỈ SỐ CÁ THỂ
7
Khái niệm: phản ánh sự biến động của từng phần
tử, từng đơn vị cá biệt.
Công thức
Chỉ số cá thể chất lượng(giá) :
Chỉ số cá thế số lượng (lượng) :
với p1, q1là mức độ kỳ nghiên cứu;
p0, q0là mức độ ở kì gốc
Đơn vị: (lần) hoặc (%)
110
0
;
pp
p
i p p
p
110
0
;
qq
q
i q q
q
CHỈ SỐ TỔNG HỢP
8
Khái niệm: phản ánh sự biến động của toàn bộ
các đơn vị, phần tử trong tổng thể nghiên cứu
Xét ví dụ
với p1, q1là mức độ kỳ nghiên cứu;
p0, q0là mức độ ở kì gốc
Đơn vị: (lần) hoặc (%)
21/01/2015
3
TÌNH HÌNH XUẤT KHẨU CỦA CÔNG TY XNĂM
2001 VÀ 2002
9
MÆt hµng
N¨m 2001 N¨m 2002
Gi¸ xuÊt
khÈu ($/t)
Lượng xuất
khẩu (t)
Gi¸ xuÊt
khÈu ($/t)
Lượng xuất
khẩu (t)
A 560 3000 545 2400
B 710 1500 710 1600
C 1130 1200 1150 1600
10
Yêu cầu: Nhận xét sự biến động về giá xuất
khẩu nói chung của doanh nghiệp
Cần giải quyết 2 vấn đề:
Tổng hợp giá cả của 3 loại hàng hoá khác
nhau
Xét riêng sự biến động của giá (không lẫn
biến động của lượng xuất khẩu)
13.3.1.2 CHỈ SỐ TOÅNG HÔÏP GIAÙ COÙ TROÏNG SOÁ (QUYEÀN SOÁ):
Ip q
p q
P
1 0
0 0 (Laspeyres)(1)
Ip q
p q
P
1
0
Ip q
p q
P
1 1
0 1 (Paasche) (2)
TRONG THÖÏC TEÁ NGÖÔØI TA THÖÔØNG DUØNG
COÂNG THÖÙC (2).
THEO VÍ DUÏ TA COÙ:
Ip q
p q
P
1 1
0 1
39530
36700 1077, = 107,7%
p q p q
1 1 0 1 39530 36700 2830
ng.ñ
11
*CAÙC COÂNG THÖÙC KHAÙC ÑEÅ TÍNH CS TOÅNG HÔÏP VEÀ GIAÙ:
Ip q
p q
p q
p
pp q
p q
p q
p
p
p q
p q
i
P
p
1 1
0 1
1 1
0
11 1
1 1
1 1
1
0
1 1
1 1
(CS TRUNG BÌNH ÑIEÀU HOAØ)
NEÁU ÑAËT: dp q
p q
11 1
1 1
thì Id
i
p
p
1
1 (neáu d1 tính baèng laàn)
hoaëc Id
i
p
p
100
1 ( neáu d1 tính baèng %)
12
21/01/2015
4
VÍ DUÏ:
107,7% 077,1
36700
39530
075,1
25800
07,1
7680
1,1
6050
2580076806050
i
qp
qp
I
p
11
11
p
Id
i
p
p
1 1
0153
1 1
0194
107
0653
1075
1077
1,
,
,
,
,
,
,
Id
i
p
p
100 100
15 3
1 1
19 4
107
65 3
1075
1077
1,
,
,
,
,
,
,
13
TRONG TRÖÔØNG HÔÏP KEÁT QUAÛ TÍNH TOAÙN
CUÛA HAI CS Laspeyres VAØ Paasche QUAÙ
CHEÂNH LEÄCH, NGÖÔØI TA SÖÛ DUÏNG CHÆ SOÁ
GIAÙ Fisher:
10
11
00
01
pqp
qp
qp
qp
I
14
15
*CAÙC COÂNG THÖÙC KHAÙC ÑEÅ TÍNH CS TOÅNG HÔÏP
KHOÁI LÖÔÏNG:
Iq p
q p
q
qq p
q p
i q p
q p
qq
1 0
0 0
1
00 0
0 0
0 0
0 0
(CS TRUNG BÌNH SOÁ HOÏC)
NEÁU ÑAËT dp q
p q
00 0
0 0
thì I i d
q q
0 (Neáu d0 tính baèng laàn)
hoaëc Ii d
qq
0
100 (Neáu d0 tính baèng %)
16
21/01/2015
5
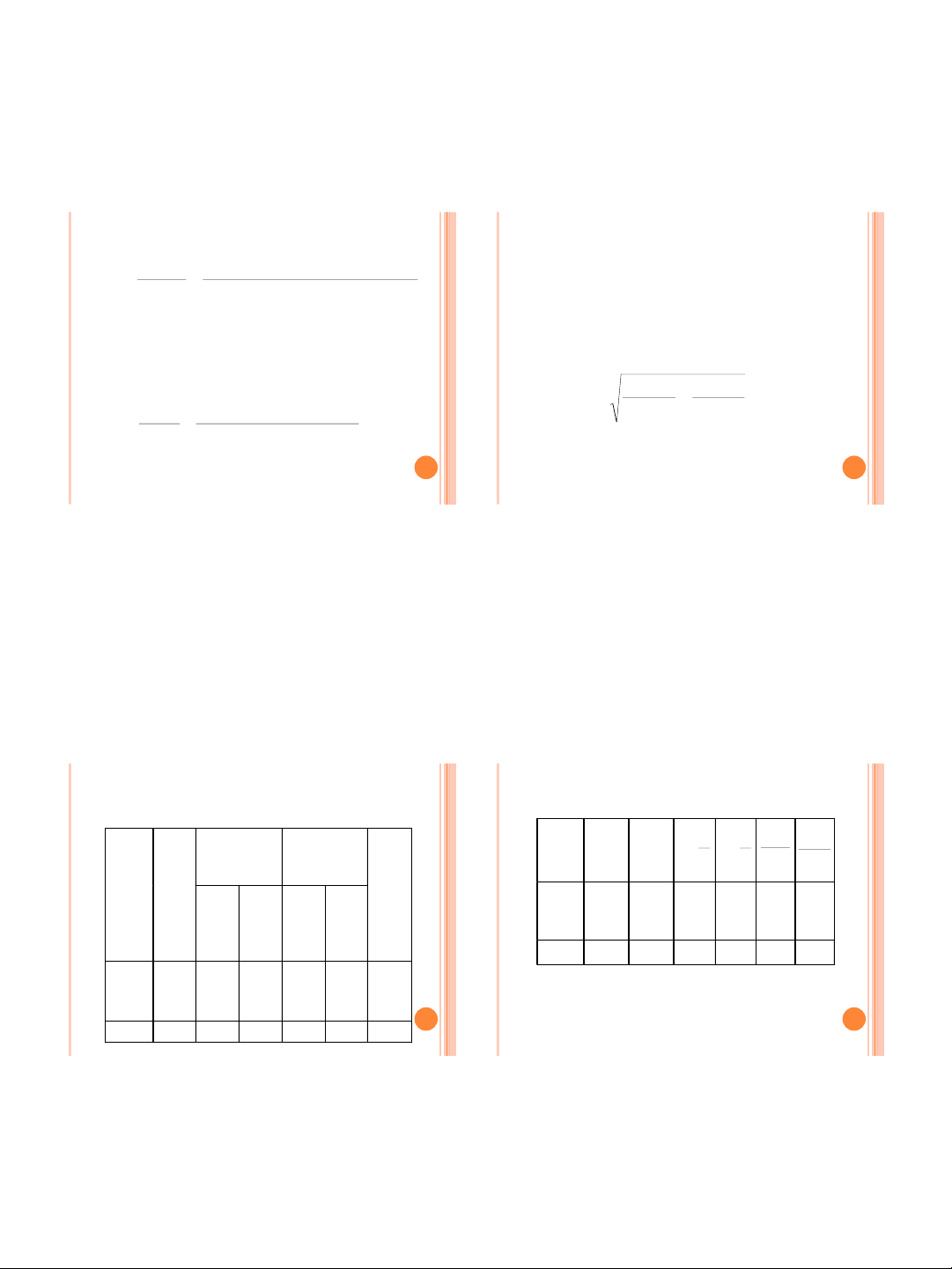
THEO VÍ DUÏ TREÂN TA COÙ:
1600060005000
160005,160002,150001,1
pq
pqi
I
00
00q
q
= 1,359 = 135,9 %
0qq diI = 1,1x0,19+1,2x0,22+1,5x0,59
= 1,359 = 135,9%
135,9%
359,1
100
595,1222,1191,1
100
di
I0q
q
17
* TRONG TRÖÔØNG HÔÏP KEÁT QUAÛ
TÍNH TOAÙN CUÛA HAI CS Laspeyres VAØ
Paasche QUAÙ CHEÂNH LEÄCH, NGÖÔØI TA
SÖÛ DUÏNG CS TOÅNG HÔÏP KHOÁI LÖÔÏNG
Fisher:
10
11
00
01
qpq
pq
pq
pq
I
18
GIAÛ SÖÛ COÙ GIAÙ CAÛ VAØ LÖÔÏNG HAØNG HOÙA
TIEÂU THUÏ TAÏI MOÄT THÒ TRÖÔØNG NHÖ SAU:
GIAÙ BAÙN
LEÛ ÑÔN VÒ
(ng.ñ)
LÖÔÏNG
HAØNG
TIEÂU THUÏ
TEÂN
HAØNG
ÑÔN
VÒ
TÍNH
KYØ
GOÁC
(p0)
KYØ
BAÙO
CAÙO
(p1)
KYØ
GOÁC
(q0)
KYØ
BAÙO
CAÙO
(q1)
p0q0
A
B
C
kg
m
l
5,0
3,0
4,0
5,5
3,2
4,3
1000
2000
4000
1100
2400
6000
5000
6000
16000
27000
19
TEÂN
HAØNG
p1q1
p0q1
iq
q
q1
0
ip
p
p1
0
d0=
p q
p q
0 0
0 0
d1=
p q
p q
1 1
1 1
A
B
C
6050
7680
25800
5500
7200
24000
1,1
1,2
1,5
1,1
1,07
1,075
0,19
0,22
0,59
0,153
0,194
0,653
39530
36700
20