Bieán ngaãu nhieân
XAÙC SUAÁT THOÁNG KEÂ
Nguyeãn Phöông
-
Ñaïi Hoïc Ngaân Haøng TPHCM
December 14, 2010
Nguyeãn Phöông - Ñaïi Hoïc Ngaân Haøng TPHCM XAÙC SUAÁT THOÁNG KEÂ
Bieán ngaãu nhieân Phaân phoái xaùc suaát
Bieán ngaãu nhieân
Ñònh nghóa
Bieán ngaãu nhieân laø moät pheùpï töông öùng moãi phaàn töû ωcuûa Ωvôùi
moät soá thöïc.
Taäp giaù trò cuûa X ñöôïc kí hieäu laø X(Ω)
Ví duï:
1Tung moät con xuùc xaéc, goïi X laø soá chaám cuûa con xuùc xaéc.
Ta coù X(Ω) = {1;2;3;4;5;6}
2Tung hai con xuùc xaéc, goïi X laø toång soá chaám cuûa hai con
xuùc xaéc. Ta coù X(Ω) = {2;3;4;5;6;7;8;9;10;11;12}
Nguyeãn Phöông - Ñaïi Hoïc Ngaân Haøng TPHCM XAÙC SUAÁT THOÁNG KEÂ
Bieán ngaãu nhieân Phaân phoái xaùc suaát
Phaân loaïi bieán ngaãu nhieân
Döïa vaøo taäp giaù trò cuûa bieán ngaãu nhieân, ta chia bieán ngaãu nhieân
laøm 2 loaïi:
Ñònh nghóa (Bieán ngaãu nhieân rôøi raïc)
Bieán ngaãu nhieân maø taäp giaù trò cuûa noù laø moät taäp höõu haïn hoaëc
voâ haïn ñeám ñöôïc, ñöôïc goïi laø bieán ngaãu nhieân rôøi raïc.
X laø bnn rôøi raïc ⇔X(Ω) = {x1,x2, . . . , xn}hoaëc
X(Ω) = {x1,x2, . . . , xn, . . .}.
Ñònh nghóa (Bieán ngaãu nhieân lieân tuïc)
Bieán ngaãu nhieân maø taäp giaù trò cuûa noù laø moät taäp voâ haïn khoâng
ñeám ñöôïc, ñöôïc goïi laø bieán ngaãu nhieân lieân tuïc.
Nguyeãn Phöông - Ñaïi Hoïc Ngaân Haøng TPHCM XAÙC SUAÁT THOÁNG KEÂ
Bieán ngaãu nhieân Phaân phoái xaùc suaát
Phaân loaïi bieán ngaãu nhieân
Ví duïï:
1Tung 3 con xuùc xaéc caân ñoái. Goïi X laø toång soá chaám cuûa 3
con xuùc xaéc. Ta coù X(Ω) = {3..18}.
2Moät ngöôøi neùm boùng vaøo roå töø vò trí caùch roå 5m ñeán khi naøo
vaøo roå thì ghi nhaän laïi soá laàn neùm boùng cuûa mình (X). Ta coù
X(Ω) = N∗.
3Ño möïc nöôùc bieån ôû moät khu vöïc cho thaáy noù chæ dao ñoäng
töø 1m ñeán 1,2m so vôùi moät moác coá ñònh. Goïi X laø möïc nöôùc
bieån (m) ôû khu vöïc ñoù taïi moät thôøi ñieåm ngaãu nhieân. Khi ñoù
X(Ω) = [1;1,2].
Nguyeãn Phöông - Ñaïi Hoïc Ngaân Haøng TPHCM XAÙC SUAÁT THOÁNG KEÂ
Bieán ngaãu nhieân Phaân phoái xaùc suaát
Phaân phoái xaùc suaát cuûa bieán ngaãu nhieân rôøi raïc
Ñònh nghóa
Phaân phoái xaùc suaát cuûa X coøn ñöôïc goïi laø baûng phaân phoái xaùc
suaát cuûa X, cho bieát khaû naêng X nhaän moãi giaù trò trong X(Ω)
töông öùng.
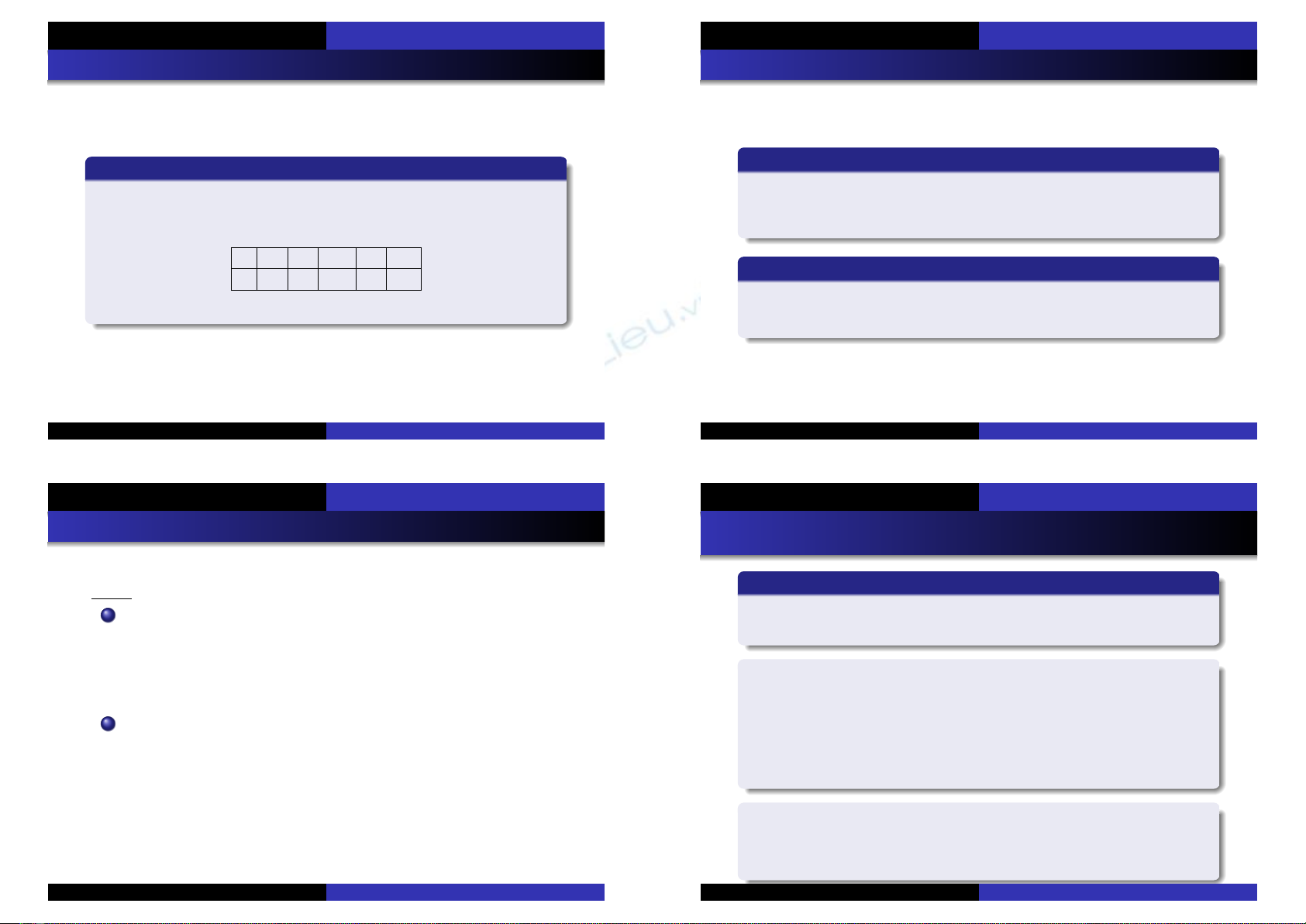
X x1x2· · · xn· · ·
P p1p2· · · pn· · ·
vôùi P(X=xi) = pi
Nguyeãn Phöông - Ñaïi Hoïc Ngaân Haøng TPHCM XAÙC SUAÁT THOÁNG KEÂ
Bieán ngaãu nhieân Phaân phoái xaùc suaát
Phaân phoái xaùc suaát cuûa bieán ngaãu nhieân rôøi raïc
Tính chaát (1)
X
i
pi=p1+· · · +pn+· · · =1.
Tính chaát (2)
P(a≤X<b) = X
a≤xi<b
pi,xi∈X(Ω).
Nguyeãn Phöông - Ñaïi Hoïc Ngaân Haøng TPHCM XAÙC SUAÁT THOÁNG KEÂ
Bieán ngaãu nhieân Phaân phoái xaùc suaát
Phaân phoái xaùc suaát cuûa bieán ngaãu nhieân rôøi raïc
Ví duï:
1Moät hoäp saûn phaåm coù 6 chính phaåm vaø 4 pheá phaåm. Laáy
ngaãu nhieân töø hoäp ra 2 saûn phaåm ñeå kieåm tra. Goïi X laø soá
pheá phaåm laáy ñöôïc.
a) Tìm phaân phoái xaùc suaát cuûa X.
b) Tính P(1≤X≤2).
2Moät ngöôøi neùm boùng töø vò trí caùch roå 5m cho ñeán khi neùm
vaøo roå thì döøng. Bieát raèng caùc laàn neùm ñoäc laäp vôùi nhau vaø
khaû naêng neùm boùng vaøo roå ôû moãi laàn neùm laø 0,3. Goïi X laø
soá laàn ngöôøi ñoù ñaõ neùm.
a) Tìm phaân phoái xaùc suaát cuûa X.
b) Tính xaùc suaát ngöôøi ñoù phaûi neùm ít nhaát 3 laàn.
Nguyeãn Phöông - Ñaïi Hoïc Ngaân Haøng TPHCM XAÙC SUAÁT THOÁNG KEÂ
Bieán ngaãu nhieân Phaân phoái xaùc suaát
Bieán ngaãu nhieân
Phaân phoái xaùc suaát
(Tröôøng hôïp lieân tuïc)
Phaân phoái xaùc suaát cuûa bieán ngaãu nhieân lieân tuïc X ñöôïc ñaëc tröng
bôûi haøm maät ñoä xaùc suaát f(x)coù caùc tính chaát sau:
f(x)≥0,∀x∈R
+∞
Z
−∞
f(x)dx =1.
P(a≤X≤b) =
b
Z
a
f(x)dx.
Nguyeãn Phöông - Ñaïi Hoïc Ngaân Haøng TPHCM XAÙC SUAÁT THOÁNG KEÂ
Bieán ngaãu nhieân Phaân phoái xaùc suaát
Bieán ngaãu nhieân lieân tuïc
Phaân phoái xaùc suaát
Ví duï:
Cho bieán ngaãu nhieân X coù haøm maät ñoä xaùc suaát:
f(x) = 0,x/∈[0;1]
cx ,x∈[0;1]
a) Xaùc ñònh c.
b) Tìm P(−1≤X≤1
2).
Nguyeãn Phöông - Ñaïi Hoïc Ngaân Haøng TPHCM XAÙC SUAÁT THOÁNG KEÂ
Bieán ngaãu nhieân Phaân phoái xaùc suaát
Bieán ngaãu nhieân
Haøm phaân phoái xaùc suaát
Ñònh nghóa (Haøm phaân phoái xaùc suaát)
Haøm phaân phoái xaùc suaát cuûa bieán ngaãu nhieân X, kí hieäu laø FX(x)
hay F(x), laø haøm ñöôïc xaùc ñònh bôûi:
F(x) = P(X<x),x∈R
Haøm phaân phoái xaùc suaát cho bieát khaû naêng X nhaän giaù trò
beân traùi x.
Neáu X laø bnnrr thì
F(x) = X
xi<x
P(X=xi) = X
xi<x
pi.
Neáu X laø bnnlt thì F(x) =
x
R
−∞
f(t)dt.
Nguyeãn Phöông - Ñaïi Hoïc Ngaân Haøng TPHCM XAÙC SUAÁT THOÁNG KEÂ
Bieán ngaãu nhieân Phaân phoái xaùc suaát
Bieán ngaãu nhieân
Haøm phaân phoái xaùc suaát
Ví duï:
1Cho bieán ngaãu nhieân rôøi raïc X coù baûng phaân phoái xaùc suaát
nhö sau: X0 1 2
P0,2 0,5 0,3
a) Tìm haøm phaân phoái xaùc suaát cuûa X.
b) Veõ ñoà thò cuûa haøm phaân phoái xaùc suaát vöøa tìm ñöôïc.
2Bieán ngaãu nhieân X coù haøm maät ñoä xaùc suaát laø:
f(x) = 2x,x∈[0;1]
0,x/∈[0;1]. Tìm haøm phaân phoái xaùc suaát cuûa
X.
Nguyeãn Phöông - Ñaïi Hoïc Ngaân Haøng TPHCM XAÙC SUAÁT THOÁNG KEÂ
Bieán ngaãu nhieân Phaân phoái xaùc suaát
Bieán ngaãu nhieân
Haøm phaân phoái xaùc suaát
Tính chaát (1)
F(x)lieân tuïc treân R.
Tính chaát (2)
F(−∞) = 0,F(+∞) = 1.
Tính chaát (3)
P(a≤X<b) = P(X<b)−P(X<a) = F(b)−F(a).
Nguyeãn Phöông - Ñaïi Hoïc Ngaân Haøng TPHCM XAÙC SUAÁT THOÁNG KEÂ