C u trúc d li u và thu t gi iấ ữ ệ ậ ả
N I DUNGỘ
CÂY NH PHÂN TÌM KI M CÂN B NGỊ Ế Ằ
C u trúc d li u và thu t gi iấ ữ ệ ậ ả
Ð nh nghĩaị
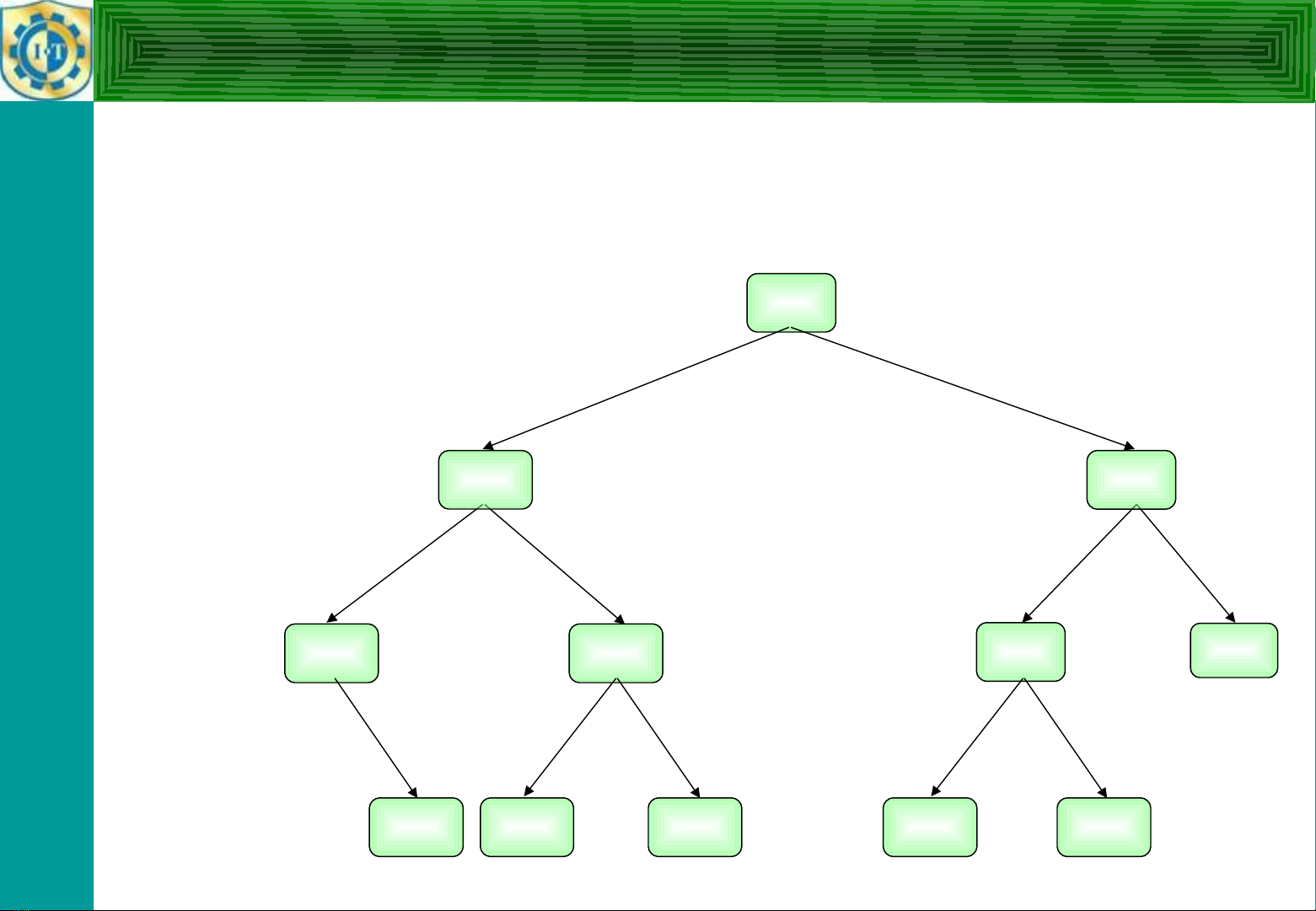
Cây nh phân tìm ki m cân b ng là câyị ế ằ mà t iạ m iỗ
nút c aủ nó độ cao c aủ cây con trái và c aủ cây con
ph iả chênh l chệ không quá m tộ
Ví d :ụ
44
23 88
13 37 59 108
15 30 40 55 71
C u trúc d li u và thu t gi iấ ữ ệ ậ ả
T ch c d li uổ ứ ữ ệ
•Chỉ số cân b ngằ = độ l chệ gi aữ cây trái và
cây ph iả c aủ m tộ nút
•Các giá trị h pợ lệ :
–CSCB( p) = 0 ⇔Độ cao cây trái ( p) = Độ
cao cây ph iả ( p)
–CSCB( p) = 1 ⇔Độ cao cây trái ( p) < Độ
cao cây ph iả ( p)
–CSCB( p) = -1 ⇔Độ cao cây trái ( p) > Độ
cao cây ph iả ( p)
C u trúc d li u và thu t gi iấ ữ ệ ậ ả
T ch c d li u(tt)ổ ứ ữ ệ
typedef struct tagAVLNode {
char balFactor; //ch s cân b ngỉ ố ằ
Data key;
struct tagAVLNode* pLeft;
struct tagAVLNode* pRight;
}AVLNode;
typedef AVLNode*AVLTree;
C u trúc d li u và thu t gi iấ ữ ệ ậ ả
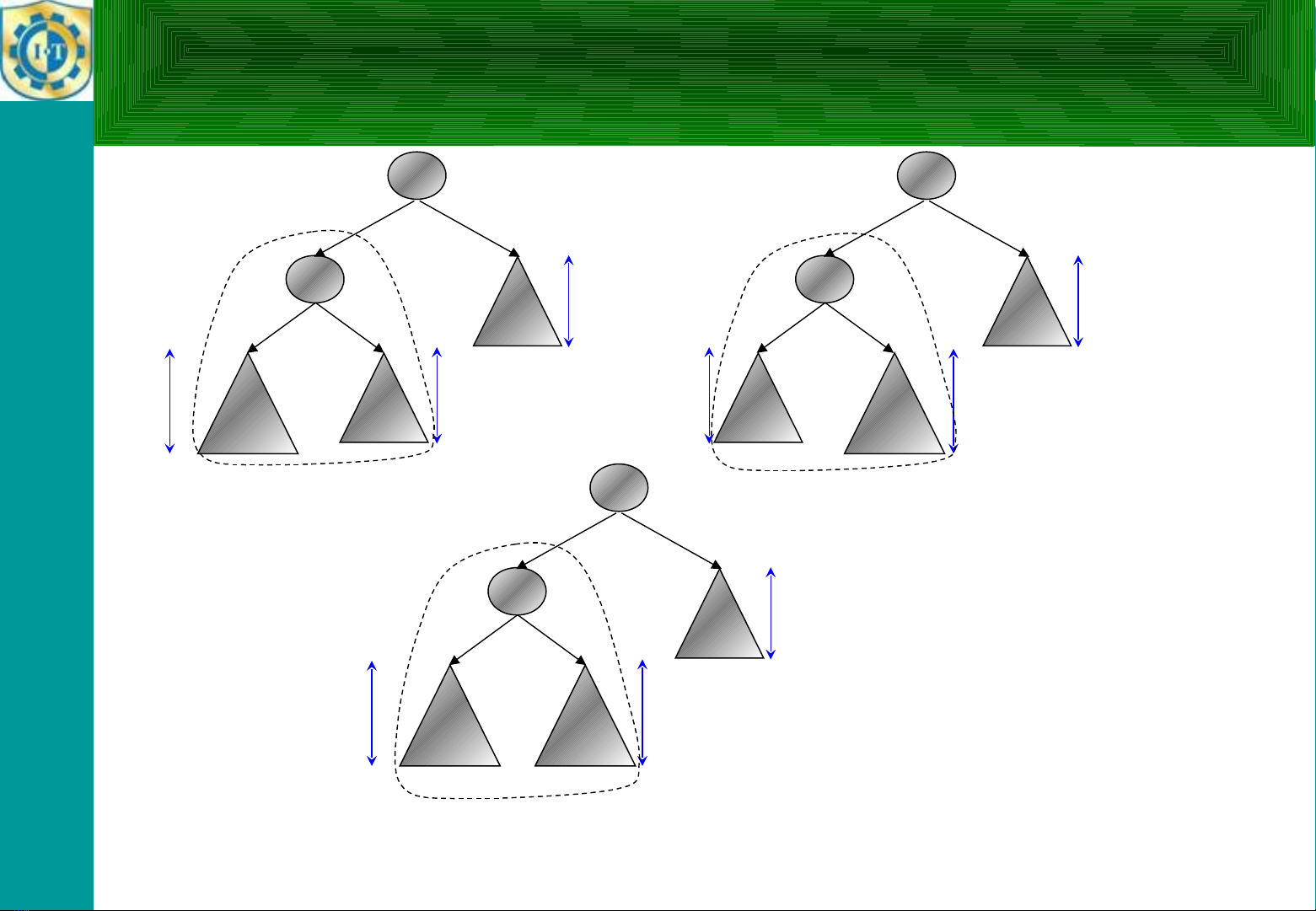
Các tr ng h p m t cân b ng do ườ ợ ấ ằ
l ch tráiệ
T
T
1
L1 R
1
h
h-1
h-1
L
R1
T
T
1
L
1
h
h-1
L
R R h-1
T
T
1
L1
h
h-1
h
L
R
L1