Số hiệu: BM1/QT-PĐBCL-RĐTV Trang: 1/2
TRƯỜNG ĐẠI HỌC SƯ PHẠM KỸ THUẬT
THÀNH PHỐ HỒ CHÍ MINH
KHOA ĐÀO TẠO CHẤT LƯỢNG CAO
NHÓM MÔN HỌC KHOA HỌC CƠ BẢN
Đ
Ề THI CUỐI KỲ HỌC KỲ I NĂM HỌC 20
22
-
202
3
Môn: Toán 2
Mã môn học: MATH132501
Đề số/Mã đề: 01. Đề thi có 02 trang.
Thời gian: 90 phút.
Được phép sử dụng tài liệu.
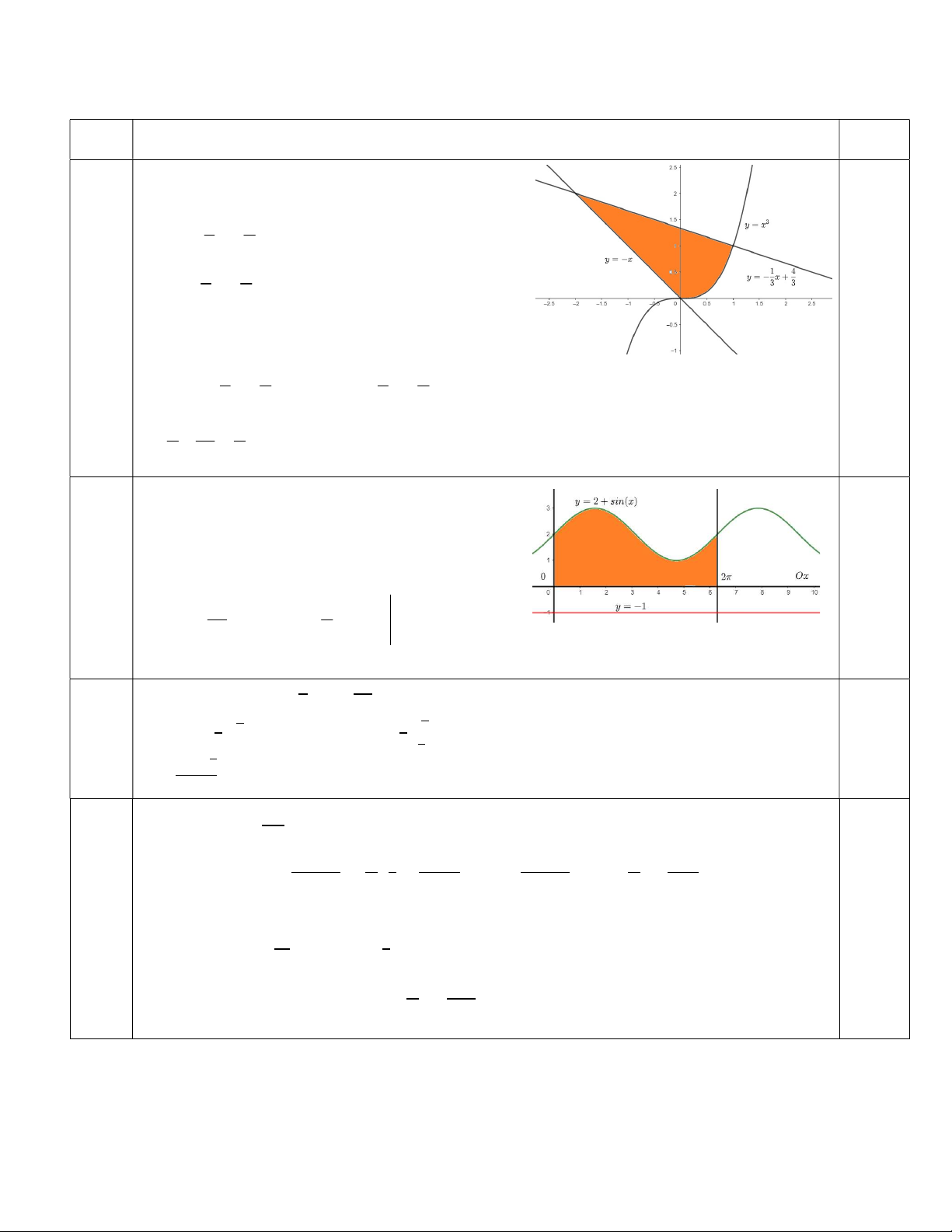
Câu 1 (1.0 điểm). Tính diện tích của hình phẳng giới hạn
bởi các đường 𝑦 = −𝑥, 𝑦 = 𝑥, 𝑦 = −
𝑥 +
(phần được tô
trong hình bên).
Câu 2 (1.0 điểm). Tính thể tích của vật thể tạo thành khi
quay hình phẳng giới hạn bởi các đường 𝑦 = 2 + sin 𝑥,
𝑦 = 0, 𝑥 = 0, 𝑥 = 2𝜋 quanh đường thẳng 𝑦 = −1.
Câu 3 (1.0 điểm). Trong hệ tọa độ cực, tính diện tích miền phẳng nằm phía trong cả hai
đường cong 𝑟 = 3 − 2 cos 𝜃 và 𝑟 = 4 cos 𝜃.
Câu 4 (1.5 điểm). Tính tích phân
2
1
1
x
x x m trong đó m là một hằng số.
Câu 5 (1.0 điểm). Giải phương trình vi phân 
 − 2𝑥𝑦 = 3𝑥𝑒 với điều kiện 𝑦(0)= 1.
Câu 6 (3.5 điểm).
a. Khảo sát sự hội tụ của các chuỗi số
2
3
3
2 1
2 10 1 1
1 ; .
5 3 1 3
k
k
k
k k
k k
A B
k
k k
b. Tìm miền hội tụ của chuỗi lũy thừa
5
1
2
3 .
k
k
k
k
x
Câu 7 (1.0 điểm). Trong
3
cho các véctơ
u i j k v i j k w i j k
2 , , 2 3 ,
a a
với a là tham số. Tìm giá trị 𝑎 > 0 để véctơ
u,
v, w
đồng phẳng.
Ghi chú: Cán bộ coi thi không được giải thích đề thi.
Chuẩn đầu ra của học phần (về kiến thức) Nội dung
kiểm tra
CLO1
Thiết lập được công thức, tính được diện tích miền phẳng, diện tích
mặt tròn xoay, thể tích vật thể, độ dài cung và giải được các bài toán
áp dụng tích phân trong vật lý.
Câu 1,2,3
CLO2 Tính được tích phân bất định, tích phân xác định, tích phân suy rộng,
và khảo sát được sự hội tụ của tích phân suy rộng. Câu 1,2,3,4
Số hiệu: BM1/QT-PĐBCL-RĐTV Trang: 2/2
CLO3 Giải được nghiệm của phương trình vi phân tuyến tính cấp 1 và áp
dụng vào các bài toán trong vật lý, kỹ thuật, đời sống. Câu 5
CLO4
Kh
ảo sát
đư
ợc
s
ự
h
ội tụ của chuỗi số, tính tổng chuỗi số.
Câu
6
CLO5 Tìm được miền hội tụ của chuỗi lũy thừa, và tìm được khai triển
Taylor/Maclaurin của một hàm số. Câu 6
CLO6 Tính được tích vô hướng và tích có hướng của 2 vectơ trong
3
, viết
được phương trình mặt phẳng và phương trình đường thẳng trong
không gian.
Câu 7
Ngày 21 tháng 05 năm 2023
Thông qua trưởng nhóm kiến thức
TS. Phạm Văn Hiển
Số hiệu: BM1/QT-PĐBCL-RĐTV
Trang 1 | 2
ĐÁP ÁN TOÁN 2 CLC THI NGÀY 30/05/2023
Câu Nội dung Điểm
1 Giao điểm:
3
0
x x x
1 4
2
3 3
x x x
31 4
1
3 3
x x x
Diện tích miền phẳng cần tìm:
0 1
3
2 0
1 4 1 4
3 3 3 3
A x x dx x x dx
4 11 9
3 12 4
0.25
0.5
0.25
2 Thể tích khối tạo thành khi quay miền
phẳng quanh
1:
y
222
0
3 sin 1
V x dx
2
2
0
17 1
2cos sin 2 17
2 4
V x x x
0.75
0.25
3 Các giao điểm
𝜃
=
,
𝜃
=
.
𝑆=2×
∫(3−2𝑐𝑜𝑠𝜃)𝑑𝜃
+
∫(4𝑐𝑜𝑠𝜃)𝑑𝜃
.
𝑆
=

√
+
5
𝜋
.
0.25
0.5
0.25
4
∫
(
𝑒
)
𝑑𝑥
=
Nếu m khác 0 thì
()=
(
−
()) và ∫󰇡
()󰇢𝑑𝑥=
ln󰇻
󰇻+𝐶 (vẫn cho
điểm nếu sv không đưa ra điều kiện của m)
Nếu m=0 thì ∫
𝑑𝑥
=lim
→󰇡−
+1󰇢=1
Nếu m
≤
-
1
thì I phân kỳ vì
lim
→
ln
󰇻
󰇻
=
∞
0.5
0.25
0.25
0.25
Số hiệu: BM1/QT-PĐBCL-RĐTV
Trang 2 | 2
Nếu m>-1 và khác 0 thì I=
+
ln
|
𝑚
+
1
|
0.25
5
𝐼
(
𝑥
)
=
𝑒
∫

=
𝑒
. Chọn một thừa số tích phân là
𝑒
.
2 2 2
2 3
3
x x x
y x e x dx C x e Ce
0 1 1
y C
23
1
x
y x e x
0.25
0.5
0.25
6. a-
A Chuỗi
3
3
2 10
5 3 1
k
k
a
k k
hội tụ khi so sánh với
1.5
1
k
do đó A hội tụ tuyệt đối
(sinh viên chỉ ra đề sai vì không tồn tại a1 thì cho 0.5 và chấm tiếp cho đủ 1 điểm)
0.25
0.5
0.25
6. a-B
Phần tử tổng quát
𝑎
=
󰇡
󰇢
>
0
với mọi
𝑘
≥
1
. Ta có
lim
→𝑎
= lim
→1
31+𝑘
𝑘
=
1
3
lim
→
1
+
1
𝑘
=
𝑒
3
<
1
.
Vậy chuỗi đã cho hội tụ theo tiêu chuẩn căn.
0.25
0.5
0.25
6. b
𝑅
=
lim
→
󰇻

󰇻
=
lim
→
(
)
(
)
(
)
=
.
Khoảng hội tụ của chuỗi là 󰇡
,
󰇢.
Tại 𝑥=
: Chuỗi trở thành ∑()
󰇡
󰇢
 =∑
 là một p-chuỗi hội tụ
Tại 𝑥=
: Chuỗi trở thành ∑()
󰇡
󰇢
 =∑()
 là một p-chuỗi đ.dấu hội tụ
Vậy tập hội tụ của chuỗi đã cho là
󰇣
,
󰇤
0.5
0.25
0.25
0.25
0.25
7
𝐮
×
𝐯
=
𝐢
𝐣
𝐤
𝑎
1
2
−1 𝑎 −1
=
⟨
−
1
−
2
𝑎
,
𝑎
−
2
,
𝑎
+
1
⟩
(𝐮×𝐯)⋅𝐰=−1−2𝑎+2𝑎−4+3𝑎+3=3𝑎−2.
(
𝐮
×
𝐯
)
⋅
𝐰
=
0
⇔
𝑎
=
(
𝑎
>
0
)
.
0.5
0.25
0.25
Số hiệu: BM1/QT-PĐBCL-RĐTV Trang: 1/2
TRƯỜNG ĐẠI HỌC SƯ PHẠM KỸ THUẬT
THÀNH PHỐ HỒ CHÍ MINH
KHOA KHOA HỌC ỨNG DỤNG
BỘ MÔN TOÁN
Đ
Ề THI CUỐI KỲ HỌC KỲ I
I
NĂM H
ỌC 20
2
2
-
202
3
Môn: Toán 2
Mã môn học: MATH132501
Đề số/Mã đề: 01. Đề thi có 02 trang.
Thời gian: 90 phút.
Được phép sử dụng tài liệu.
Câu 1 (1.5 điểm). Cho miền phẳng D được giới hạn bởi parabol
𝑦 = 𝑥, nửa cung tròn 𝑦 = √2𝑥−𝑥 và trục hoành (phần tô đậm
trong Hình 1).
Tính thể tích tròn xoay tạo thành khi quay D quanh trục hoành.
Câu 2 (1.0 điểm). Trong hệ tọa độ cực, tính diện tích miền phẳng nằm
giữa đường cong 𝑟 = 1− 2cos𝜃 và 𝑟 = 2.
(phần tô đậm như trong Hình 2).
Câu 3 (3.0 điểm).
a. Tính tích phân suy rộng
𝐼 = (2𝑥+3)ln (𝑥)𝑑𝑥
.
b. Tìm hằng số α > 0 sao cho tích phân suy rộng sau hội tụ
5+3cos𝑥
𝑥
𝑑𝑥.
c. Giải phương trình vi phân 𝑦󰆒+2𝑥𝑦 = 2𝑥.
Câu 4 (3.5 điểm).
a. Tính tổng của chuỗi cấp số nhân sau (nếu nó hội tụ)
𝑆 = 2
9−√8
27 +4
81−√32
243 +⋯
b. Tìm bán kính hội tụ và miền hội tụ của chuỗi lũy thừa sau:
2
4
1
1
5
2 ( 3)
k
k
k
kx
k
.
c. Khai triển chuỗi Maclaurin hàm số sau đây (yêu cầu nêu rõ khoảng hội tụ)
2
( )
2
x
f x
x
.
Câu 5 (1.0 điểm). Trong không gian cho tam giác có ba đỉnh là 𝐴(3,1,3),𝐵(4,3,5) và
𝐶(−2,3,1−𝑎) với số thực 𝑎 > 0. Tìm giá trị của 𝑎 để diện tích tam giác 𝐴𝐵𝐶 bằng 9.
Ghi chú: Cán bộ coi thi không được giải thích đề thi.