[www.VIETMATHS.com]
S GIÁO D C VÀ ĐÀO T OỞ Ụ Ạ ĐỀ THI TUY N SINH L P 10 THPTỂ Ớ
B C GIANG ẮNĂM H C 2012-2013Ọ
Môn thi : Toán
Th i gian : 120 phút không k th i gian giao đ ờ ể ờ ề
Ngày thi 30 tháng 6 năm 2012
Câu 1. (2 đi m)ể
1.Tính
12
2 1
-
-
2 .Xác đ nh giá tr c a a,bi t đ th hàm s y = ax - 1 đi qua đi m M(1;5)ị ị ủ ế ồ ị ố ể
Câu 2: (3 đi m)ể
1.Rút g n bi u th c: ọ ể ứ
1 2 3 2
( ).( 1)
2 2 2
a a
Aa a a a
- +
= - +
- - -
v i a>0,aớ
4ﾹ
2.Gi i h pt: ả ệ
2 5 9
3 5
x y
x y
ﾹ- =
ﾹ
ﾹ
ﾹ
ﾹ+ =
ﾹ
ﾹ
3. Ch ng minh r ng pt: ứ ằ
2
1 0x mx m+ + - =
luôn có nghi m v i m i giá tr c a m.ệ ớ ọ ị ủ
Gi s xả ử 1,x2 là 2 nghi m c a pt đã cho,tìm giá tr nh nh t c a bi u th cệ ủ ị ỏ ấ ủ ể ứ
2 2
1 2 1 2
4.( )B x x x x= + - +
Câu 3: (1,5 đi m)ể
M t ôtô t i đi t A đ n B v i v n t c 40km/h. Sau 2 gi 30 phút thì m t ôtô taxi cũng xu t phát đi t Aộ ả ừ ế ớ ậ ố ờ ộ ấ ừ
đ n B v i v n t c 60 km/h và đ n B cùng lúc v i xe ôtô t i.Tính đ dài quãng đ ng AB.ế ớ ậ ố ế ớ ả ộ ườ
Câu 4: (3 đi m)ể
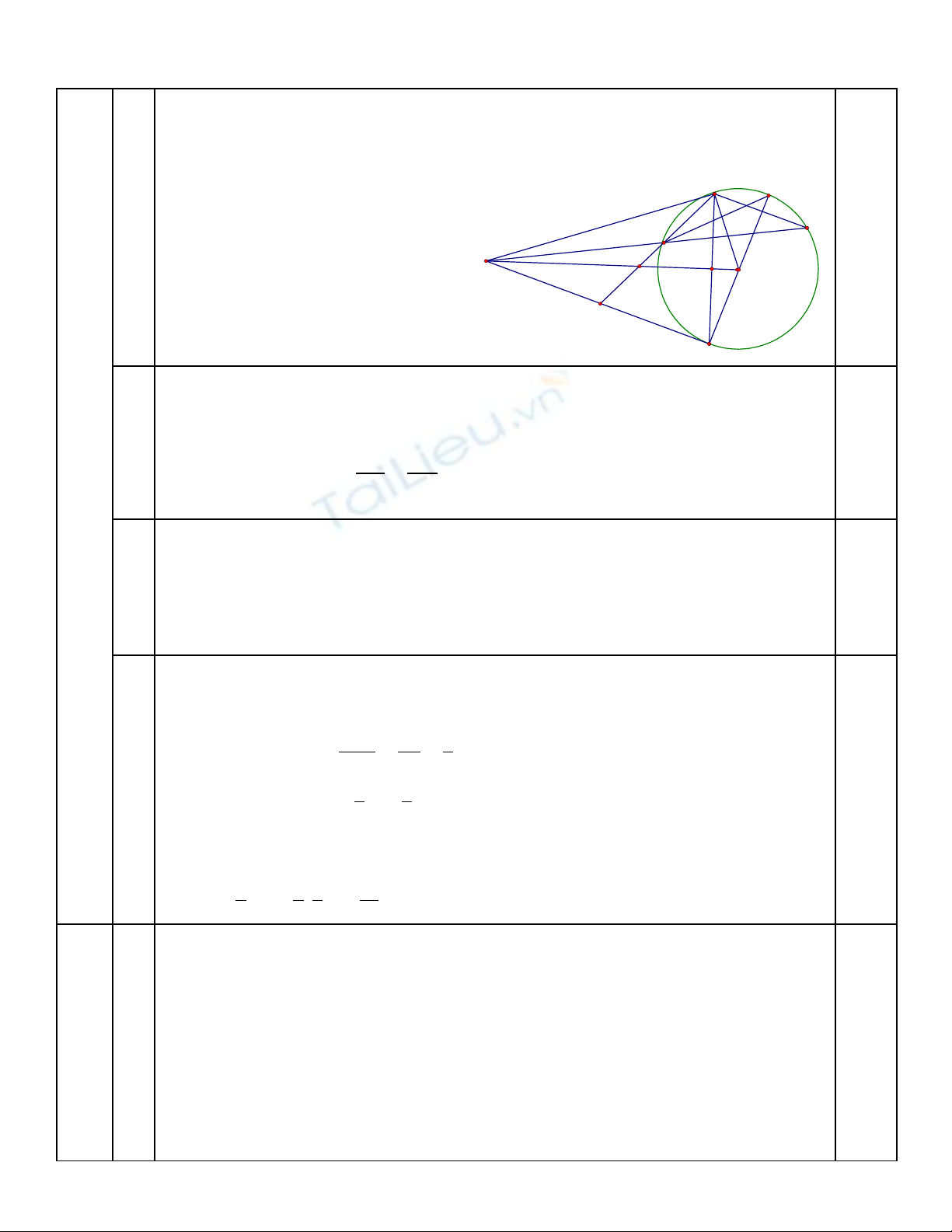
Cho đ ng tròn (O) và m t đi m A sao cho OA=3R. Qua A k 2 ti p tuy n AP và AQ c a đ ng trònườ ộ ể ẻ ế ế ủ ườ
(O),v i P và Q là 2 ti p đi m.L y M thu c đ ng tròn (O) sao cho PM song song v i AQ.G i N là giaoớ ế ể ấ ộ ườ ớ ọ
đi m th 2 c a đ ng th ng AM và đ ng tròn (O).Tia PN c t đ ng th ng AQ t i K.ể ứ ủ ườ ẳ ườ ắ ườ ẳ ạ
1.Ch ng minh APOQ là t giác n i ti p.ứ ứ ộ ế
2.Ch ng minh KAứ2=KN.KP
3.K đ ng kính QS c a đ ng tròn (O).Ch ng minh tia NS là tia phân giác c a gócẻ ườ ủ ườ ứ ủ
ﾹ
PNM
.
4. G i G là giao đi m c a 2 đ ng th ng AO và PK .Tính đ dài đo n th ng AG theo bán kính R.ọ ể ủ ườ ẳ ộ ạ ẳ
Câu 5: (0,5đi m)ể
Cho a,b,c là 3 s th c khác không và tho mãn:ố ự ả
2 2 2
2013 2013 2013
( ) ( ) ( ) 2 0
1
a b c b c a c a b abc
a b c
ﾹ
ﾹ+ + + + + + =
ﾹ
ﾹ
ﾹ+ + =
ﾹ
ﾹ
Hãy tính giá tr c a bi u th c ị ủ ể ứ
H NG D N CH M (tham kh o)ƯỚ Ẫ Ấ ả
Câu Ý N i dungộĐi mể
1 1
2
1 2 1 2 1
2 2 2 2 1 2 1
2 1 ( 2 1).( 2 1) ( 2) 1)
+ +
- = - = - = + - =
- - + -
KL:
1
Tr n H i Nam - Tell: 01662 843844 – TT luy n thi T m Cao M i Tell: 01684 356573 – 0533564384 – 0536513844 – 0944323844ầ ả ệ ầ ớ 1
Đ CHÍNH TH CỀ Ứ
[www.VIETMATHS.com]
2 Do đ th hàm s y = ax-1 đi qua M(1;5) nên ta có a.1-1=5ồ ị ố
ﾹ
a=6
KL:
1
2 1
2 ( 1).( 2)
( ).( 1)
( 2) ( 2) 2
2 1
( ).( 1 1) . 1
( 2)
a a a
Aa a a a a
aa a
a a a
- -
= - + =
- - -
-
= - + = =
-
KL:
0,5
0,5
2
2 5 9 2 5 9 2 5 9 1
3 5 15 5 25 17 34 2
x y x y x y y
x y x y x x
� � � �
- = - = - = = -
� � � �
� � � �
� � �
� � � �
� � � �
+ = + = = =
� � � �
� � � �
KL:
1
3 Xét Pt:
2
1 0x mx m+ + - =
2 2 2
Δ 4( 1) 4 4 ( 2) 0m m m m m= - - = - + = - ﾹ
V y pt luôn có nghi m v i m i mậ ệ ớ ọ
Theo h th c Viet ta cóệ ứ
1 2
1 2
1
x x m
x x m
ﾹ+ = -
ﾹ
ﾹ
ﾹ
ﾹ= -
ﾹ
ﾹ
Theo đ bàiề
2 2 2
1 2 1 2 1 2 1 2 1 2
2 2 2
2
4.( ) ( ) 2 4.( )
2( 1) 4( ) 2 2 4 2 1 1
( 1) 1 1
B x x x x x x x x x x
m m m m m m m m
m
= + - + = + - - +
= - - - - = - + + = + + +
= + + ﾹ
V y minB=1 khi và ch khi m = -1ậ ỉ
KL:
0,25
0,25
0,5
3 G i đ dài quãmg đ ng AB là x (km) x>0ọ ộ ườ
Th i gian xe t i đi t A đ n B là ờ ả ừ ế
40
x
h
Th i gian xe Taxi đi t A đ n B là :ờ ừ ế
60
x
h
Do xe t i xu t phát tr c 2h30phút = ả ấ ướ
5
2
nên ta có pt
5
40 60 2
3 2 300
300
x x
x x
x
- =
- =�
=�
Giá tr x = 300 có tho mãn ĐK ị ả
V y đ dài quãng đ ng AB là 300 km.ậ ộ ườ
0,25
0,25
0,25
0,25
0,25
0,25
4 1
Xét t giác APOQ có ứ
ﾹ
0
90APO =
(Do AP là ti p tuy n c a (O) P)ế ế ủ ở
Tr n H i Nam - Tell: 01662 843844 – TT luy n thi T m Cao M i Tell: 01684 356573 – 0533564384 – 0536513844 – 0944323844ầ ả ệ ầ ớ 2
[www.VIETMATHS.com]
ﾹ
0
90AQO =
(Do AQ là ti p tuy n c a (O) Q)ế ế ủ ở
ﾹ
ﾹ
0
180APO AQO+ =�
,mà hai góc này là 2 góc đ i nên t giác APOQ là t giác n iố ứ ứ ộ
ti p ế
0,75
2Xét
Δ
AKN và
Δ
PAK có
ﾹ
AKP
là góc chung
ﾹ
ﾹ
APN AMP=
( Góc nt……cùng ch n cung NP)ắ
Mà
ﾹ
ﾹ
NAK AMP=
(so le trong c a PM //AQủ
Δ
AKN ~
Δ
PKA (gg)
2
.
AK NK AK NK KP
PK AK
= =� �
(đpcm)
0,75
3 K đ ng kính QS c a đ ng tròn (O)ẻ ườ ủ ườ
Ta có AQ
^
QS (AQ là tt c a (O) Q)ủ ở
Mà PM//AQ (gt) nên PM
^
QS
Đưng kính QS ờ
^
PM nên QS đi qua đi m chính gi a c a cung PM nhể ữ ủ ỏ
ﾹ
ﾹ
sd PS sd SM=
ﾹ
ﾹ
PNS SNM=�
(hai góc nt ch n 2 cung b ng nhau)ắ ằ
Hay NS là tia phân giác c a góc PNMủ
0,75
4Ch ng minh đ c ứ ượ
Δ
AQO vuông Q, có QGở
^
AO(theo Tính ch t 2 ti p tuy n c tấ ế ế ắ
nhau)
Theo h th c l ng trong tam giác vuông ta cóệ ứ ượ
2 2
2
1
.3 3
1 8
33 3
OQ R
OQ OI OA OI R
OA R
AI OA OI R R R
= = = =�
= - = - =�
Do
Δ
KNQ ~
Δ
KQP (gg)
2
.KQ KN KP=�
mà
2
.AK NK KP=
nên AK=KQ
V y ậ
Δ
APQ có các trung tuy n AI và PK c t nhau G nên G là tr ng tâmế ắ ở ọ
2 2 8 16
.
3 3 3 9
AG AI R R= = =�
0,75
5 Ta có:
2 2 2
2 2 2 2 2 2
2 2 2 2 2 2
2 2
2
( ) ( ) ( ) 2 0
2 0
( ) ( ) (2 ) 0
( ) ( ) ( ) 0
( )( ) 0
( ).( ).( ) 0
a b c b c a c a b abc
a b a c b c b a c a c b abc
a b b a c a c b abc b c a c
ab a b c a b c a b
a b ab c ac bc
a b a c b c
+ + + + + + =
+ + + + + + =�
+ + + + + + =�
+ + + + + =�
+ + + + =�
+ + + =�
*TH1: n u a+ b=0 ế
0,25
0,25
Tr n H i Nam - Tell: 01662 843844 – TT luy n thi T m Cao M i Tell: 01684 356573 – 0533564384 – 0536513844 – 0944323844ầ ả ệ ầ ớ 3
G
K
N
S
M
I
Q
P
A
O
[www.VIETMATHS.com]
Ta có
2013 2013 2013
1
1
a b a b
c
a b c
ﾹﾹ
= - = -
ﾹﾹ
� �
ﾹ
� �
� �=
+ + = ﾹ
ﾹ
ﾹ
ﾹ
ta có
2013 2013 2013
1 1 1 1Qa b c
= + + =
Các tr ng h p còn l i xét t ng tườ ợ ạ ươ ự
V y ậ
2013 2013 2013
1 1 1 1Qa b c
= + + =
“B dày th i gian t n t i – Ch t l ng giáo viên, lòng nhi t tình - S l ng l n h c sinh theo h c vàề ờ ồ ạ ấ ượ ệ ố ượ ớ ọ ọ
đ t thành tích cao- S l ng tài li u kh ng l đ c h c sinh, giáo viên, ph huynh s d ng CHÍNHạ ố ượ ệ ổ ồ ượ ọ ụ ử ụ
LÀ NI M T HÀO, S KH NG Đ NH C A TT GIA S – TT LUY N THI T M CAO M I”Ề Ự Ự Ẳ Ị Ủ Ư Ệ Ầ Ớ
- Các em h c sinh trên đ a bàn Đông Hà (Qu ng Tr ) và các huy n lân c n (Cam L , Tri u Phong, Gioọ ị ả ị ệ ậ ộ ệ
Linh,…) hoàn toàn có th đăng kí và h c t i nhà, đ đ c h ng d n c th các em hãy g i theo sể ọ ạ ể ượ ướ ẫ ụ ể ọ ố
máy trung tâm. Ngoài ra các em có th h c t i trung tâm ho c h c t i nhà các giáo viên c a trung tâm.ể ọ ạ ặ ọ ạ ủ
- Các em có th đăng kí h c các môn: Toán, Lý, Hóa, Sinh, Anh, Văn (các kh i 9-12, Luy n thi đ i h cế ọ ố ệ ạ ọ
c p t c, luy n thi vào l p 10 c p t c, luy n thi t t nghi p 12 c p t c). Riêng các l p h c t kh i 8ấ ố ệ ớ ấ ố ệ ố ệ ấ ố ớ ọ ừ ố
tr xu ng, ph huynh hay h c sinh nào yêu c u trung tâm s cho giáo viên phù h p v d y kèm cácở ố ụ ọ ầ ẽ ợ ề ạ
em
- Đ i v i giáo viên muôn tham gia trung tâm hãy đi n tho i đ bi t thêm chi ti t c thố ớ ệ ạ ể ế ế ụ ể
M I CHI TI T XIN LIÊN H 01662 843 844 Ọ Ế Ệ – 0533 564384 – 0536 513844 – 0944323844
Tr n H i Nam - Tell: 01662 843844 – TT luy n thi T m Cao M i Tell: 01684 356573 – 0533564384 – 0536513844 – 0944323844ầ ả ệ ầ ớ 4