
Ph n 2: dùng stack đ kh thu t tóan đ quy nhánhầ ể ử ậ ệ
Nh chúng ta đã bi t, s th c hi n c a đ quy chính là s th c hi n l i chính b n thânư ế ự ự ệ ủ ệ ự ự ệ ạ ả
nó v i d li u nh h n, nên khi g i hàm đ quy thì máy s c p phát m t vùng nh có cớ ữ ệ ỏ ơ ọ ệ ẽ ấ ộ ớ ơ
ch ho t đ ng nh Stack (ngăn x p) cho hàm đ quy đó. C ch này ho t đ ng nhế ạ ộ ư ế ệ ơ ế ạ ộ ư
ki u LIFO( last in first out – vào sau ra tr c), t c là vi c thêm vào hay l y ra đ u th cể ướ ứ ệ ấ ề ự
hi n thông qua m t đ u ra duy nh tệ ộ ầ ấ
N u m t ch ng trình con đ qui P(x) đ c g i t ch ng trình chính ta nói ch ngế ộ ươ ệ ượ ọ ừ ươ ươ
trình con đ c th c hi n m c 1. Ch ng trình con này g i chính nó, ta nói nó đi sâuượ ự ệ ở ứ ươ ọ
vào m c 2... và cho đ n m t m c k. Rõ ràng m c k ph i th c hi n xong thì m c k-1 m iứ ế ộ ứ ứ ả ự ệ ứ ớ
đ c th c hi n ti p t c, hay ta còn nói là ch ng trình con quay v m c k-1.ượ ự ệ ế ụ ươ ề ứ
Trong khi m t ch ng trình con t m c i đi vào m c i+1 thì các bi n c c b c a m c iộ ươ ừ ứ ứ ế ụ ộ ủ ứ
và đ a ch c a mã l nh còn dang d ph i đ c l u tr , đ a ch này g i là đ a ch tr v .ị ỉ ủ ệ ở ả ượ ư ữ ị ỉ ọ ị ỉ ở ề
Khi t m c i+1 quay v m c i các giá tr đó đ c s d ng. Nh v y nh ng bi n c c bừ ứ ề ứ ị ượ ử ụ ư ậ ữ ế ụ ộ
và đ a ch l u sau đ c dùng tr c. Tính ch t này g i ý cho ta dùng m t stack đ l u giị ỉ ư ượ ướ ấ ợ ộ ể ư ữ
các giá tr c n thi t c a m i l n g i t i ch ng trình con nh ị ầ ế ủ ỗ ầ ọ ớ ươ ư bi n c c b , các tham sế ụ ộ ố.
M i khi lùi v m t m c thì các giá tr này đ c l y ra đ ti p t c th c hi n m c này. Taỗ ề ộ ứ ị ượ ấ ể ế ụ ự ệ ứ
tóm t t quá trình:ắ
• B óc 1: T o 1 stack r ng ư ạ ỗ
• B óc 2: L u các tham s hình th c m c 1 vào stack.ư ư ố ứ ở ứ
• B c 3: L p cho đ n khi stack r ng ướ ặ ế ỗ
1. L y ra 1 ph n t X kh i stack ấ ầ ử ỏ
Vào sau
Vào tr cướ
vào ra
Đ nhỉ
Stack(Ngăn x pế)
2. N u X tho đi u ki n d ng c a đ qui (NEO) thì x lý d li uế ả ề ệ ừ ủ ệ ử ữ ệ
Ng c l i (ph n đ qui) ượ ạ ầ ệ
X lý theo thu t tóan ử ậ
Xác đ nh l i g i đ quy v i các tham s t ng ng vàị ờ ọ ệ ớ ố ươ ứ
n p các tham s đó vào stackạ ố
B c 4: K t thúc thu t toánướ ế ậ
M t s ví d v dùng Stack đ kh đ quiộ ố ụ ề ể ử ệ
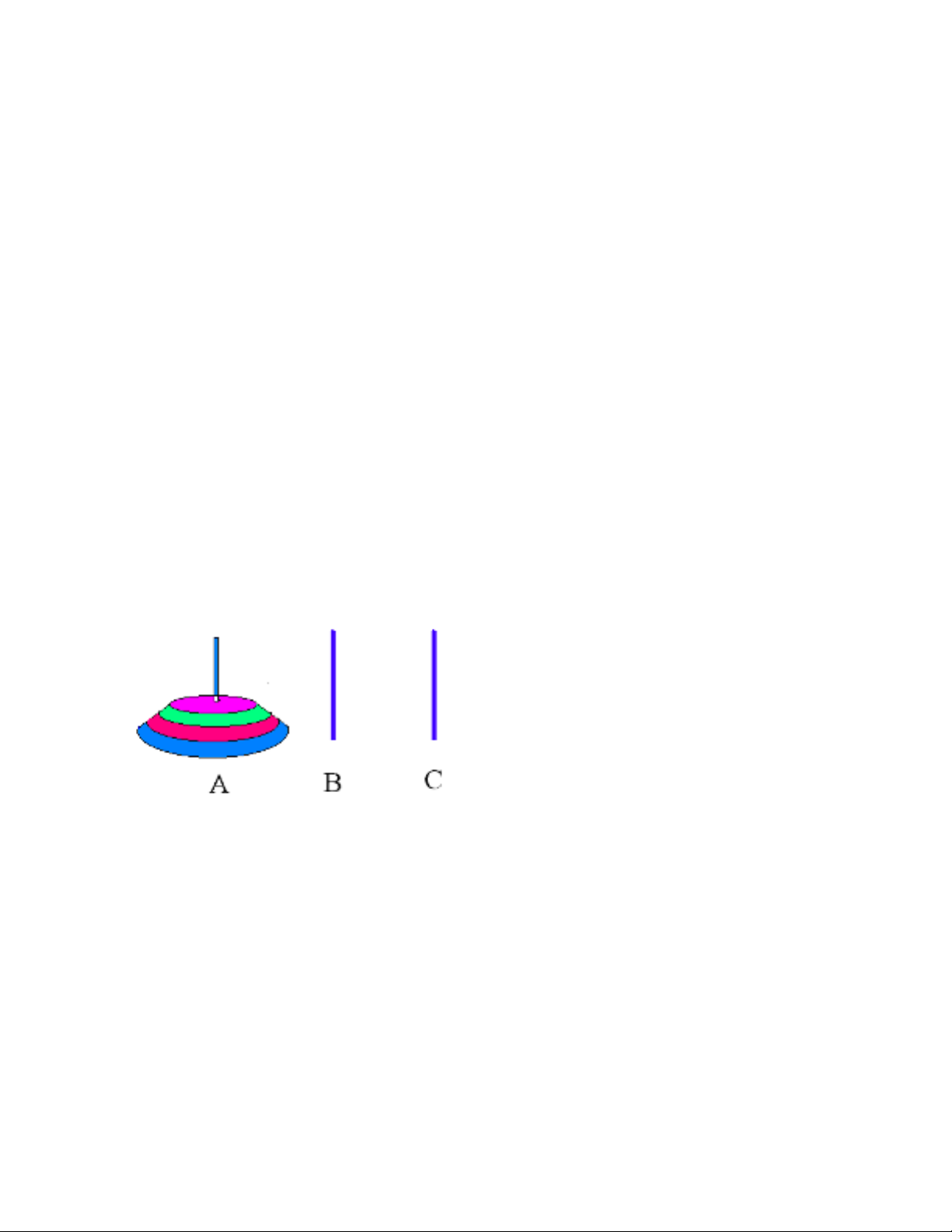
Ví d 1: Bài toán Tháp Hà N iụ ộ
Có ba c c A,B,C. Kh i đ u c c A có m t s đĩa x p theo th t nh d n lên trên đ nh.ọ ở ầ ọ ộ ố ế ứ ự ỏ ầ ỉ
Bài toán đ t ra là ph i chuy n toàn b ch ng đĩa t A sang C. M i l n th c hi n chuy nặ ả ể ộ ồ ừ ỗ ầ ự ệ ể
m t đĩa t m t c c sang m t c c khác và không đ c đ t đĩa l n n m trên đĩa nhộ ừ ộ ọ ộ ọ ượ ặ ớ ằ ỏ
Phân tích bài toán:
Tr ng h p 1 đĩa: Chuy n th ng t A sang C. Đây là tr ng h p suy bi n ườ ợ ể ẳ ừ ườ ợ ế
Tr ng h p 2 đĩa: ườ ợ Chuy n 1 đĩa t A sang Bể ừ
Chuy n 1 đĩa t A sang Cể ừ
Chuy n 1 đĩa t B sang Cể ừ
Tr ng h p chung n>1 đĩa; Ta coi n-1 đĩa trên nh là 1 đĩa và ta áp d ng trong tr ngườ ợ ư ụ ườ
h p 2 đĩaợ

Chuy n n-1 đĩa t A sang B ( dùng c c C làm trung gian)ể ừ ọ
Chuy n 1 đĩa t A sang Cể ừ
Chuy n n-1 đĩa t B sang C (dùng c c A làm trung gian)ể ừ ọ
thu t toán đ qui mô ph ng nh sau:ậ ệ ỏ ư
Proc Move(n,A,B,C) // Chuy n n đĩa t c c A sang c c C ể ừ ọ ọ
If n=1 Then
chuy n (A,’ể’,C)
Else { Call Move(n-1, A, C, B)
Call Move(1, A, B, C)
Call Move(n-1, B, A, C)
}
Return
Quá trình th c hi n ch ng trình con đ c minh ho v i 3 đĩa (n=3) nh sau:ự ệ ươ ượ ạ ớ ư
Move(1,A,B,C) A->B
Move(2,A,C,B) Move(1,A,C,B) A->C
Move(1,B,C,A) B->C
move(3,A,B,C) Move(1,A,B,C) A->B
Move(1,C,A,B) C->A
Move(2,C,B,A) Move(1,C,B,A) C->B
Move(1,A,B,C) A->B
M c 1ứm c 2ứm c 3ứ
Cây đ quy trên đ c mô ph ng qua vi c dùng stack đ gi i quy t nh sau:ệ ượ ỏ ệ ể ả ế ư
(3,A,B,C) (2,A,C,B) Quá trình chuy n đĩaể
(2,B,A,C)
T đây, ta xây d ng c u trúc c a m i ph n t đ c l u trong stack đ gi i quy t bàiừ ự ấ ủ ỗ ầ ử ượ ư ể ả ế
toán tháp Hà n i nh sau:ộ ư
struct Item_Tower{
int num; // s đĩaố
char sour, midl, dest;
void assign(int n, char a, char b, char c){ // hàm gán t ng giá tr cho các thu c tínhừ ị ộ
num = n; sour = a; midl = b, dest = c;
}
};
Thu t toán kh đ quiậ ử ệ
3 A B C
A->C
A->B
C->B
A->C
B->A
B->C
A->C
2ACB1ABC2BAC 1ABC1ACB1CAB
1ABC2BAC
2BAC 1BCA1BAC1ABC
void haNoi_Tower(int n, char a, char b, char c){
Stack<Item_Tower> sTower; // Khai báo stack ki u Item_Towerể
Item_Tower t;
int d = 0;
t.assign(n, a, b, c);
sTower.push(t);
while (sTower.isEmpty() == false){
Item_Tower temp = sTower.topOfStack();
sTower.pop();
if(temp.num == 1) cout<<" \n "<<++d<<" ."<<temp.sour <<" ----->"<<temp.dest;
else{
t.assign(temp.num-1, temp.midl, temp.sour, temp.dest);
sTower.push(t);
t.assign(1, temp.sour, temp.midl, temp.dest);
sTower.push(t);
t.assign(temp.num - 1, temp.sour, temp.dest, temp.midl);
sTower.push(t);
}
}
}
Ví d 2: Ph bàn c kích th c 2ụ ủ ờ ướ n * 2n b ng các con trominoằ
Yêu c u: có bàn c kích th c 2ầ ờ ướ n * 2n (n nguyên >0). Đánh d u 1 ô b t kỳ trên bàn c ,ấ ấ ờ
sau đó dùng các con tromino ph đ y bàn c .ủ ầ ờ


























