GIAÍI TÊCH MAÛNG
Trang 128
8.6. CAÏC HÃÛ THÄÚNG ÂIÃÖU CHÈNH VAÌ BÄÜ KÊCH TÆÌ.
Trong kyî thuáût giaíi quyãút âaî mä taí trong pháön 8.5 aính hæåíng cuía bäü kêch tæì vaì
hãû thäúng âiãöu khiãøn van âiãöu chènh lãn sæû phaín æïng cuía hãû thäúng cäng suáút âæåüc boí
qua. Trong âàûc træng âoï âiãûn aïp kêch tæì Efd vaì cäng suáút cå Pm âæåüc giæî khäng âäøi trong
viãûc tênh toaïn quaï trçnh quaï âäü khi yãu cáöu sæû âaïnh giaï chi tiãút viãûc phaín æïng laûi cuía hãû
thäúng hoàûc thåìi gian phán têch keïo daìi hån 1 giáy thç viãûc kãø âãún aính hæåíng cuía bäü kêch
tæì vaì hãû thäúng van âiãöu chènh ráút quan troüng.
Hãû thäúng âiãöu khiãøn kêch tæì cung cáúp âiãûn aïp kêch tæì thêch håüp âãø duy trç âiãûn aïp
cuía hãû thäúng theo mong muäún, thæåìng laì taûi thanh goïp âiãûn aïp cao cuía nhaì maïy âiãûn.
Mäüt âàûc træng quan troüng cuía hãû thäúng âiãöu khiãøn kêch tæì laì khaí nàng âaïp æïng mäüt caïch
nhanh choïng âäúi våïi âäü lãûch âiãûn aïp trong caí hai quaï trçnh âiãöu khiãøn hãû thäúng bçnh
thæåìng vaì hãû thäúng åí tçnh traûng sæû cäú tráöm troüng. Nhiãöu kiãøu hãû thäúng âiãöu khiãøn kêch
tæì khaïc nhau âæåüc sæí duûng trong hãû thäúng cäng suáút. Nhæîng thaình pháön cå baín cuía hãû
thäúng âiãöu khiãøn kêch tæì âoï laì bäü âiãöu chènh, bäü khuãúch âaûi vaì bäü kêch tæì. Bäü âiãöu chènh
âo âiãûn aïp âiãöu chènh thæûc vaì xaïc âënh âäü lãûch âiãûn aïp. Tên hiãûu âäü lãûch sinh ra båíi bäü
âiãöu chènh thç sau âoï âæåüc khuãúch âaûi cung cáúp tên hiãûu yãu cáöu thay âäøi doìng âiãûn kêch
tæì. Âiãöu naìy âæåüc laìm cho âãún khi taûo ra sæû thay âäøi âiãûn aïp âáöu ra cuía bäü kêch tæì. Sæû
thay âäøi naìy æïng våïi kãút quaí cuía mäüt mæïc kêch tæì måïi âäúi våïi nguäön phaït âiãûn. Mäüt
hçnh thæïc thuáûn tiãûn cuía sæû âàûc træng hãû thäúng âiãöu khiãøn laì mäüt daîy så âäö khäúi liãn hãû
qua caïc chæïc nàng chuyãøn âäøi biãún säú âáöu vaìo vaì säú âáöu ra cuía caïc thaình pháön chênh
yãúu cuía hãû thäúng. Daîy så âäö khäúi duìng âãø âàûc træng âån giaín hoïa sæû hoaût âäüng liãn tuûc
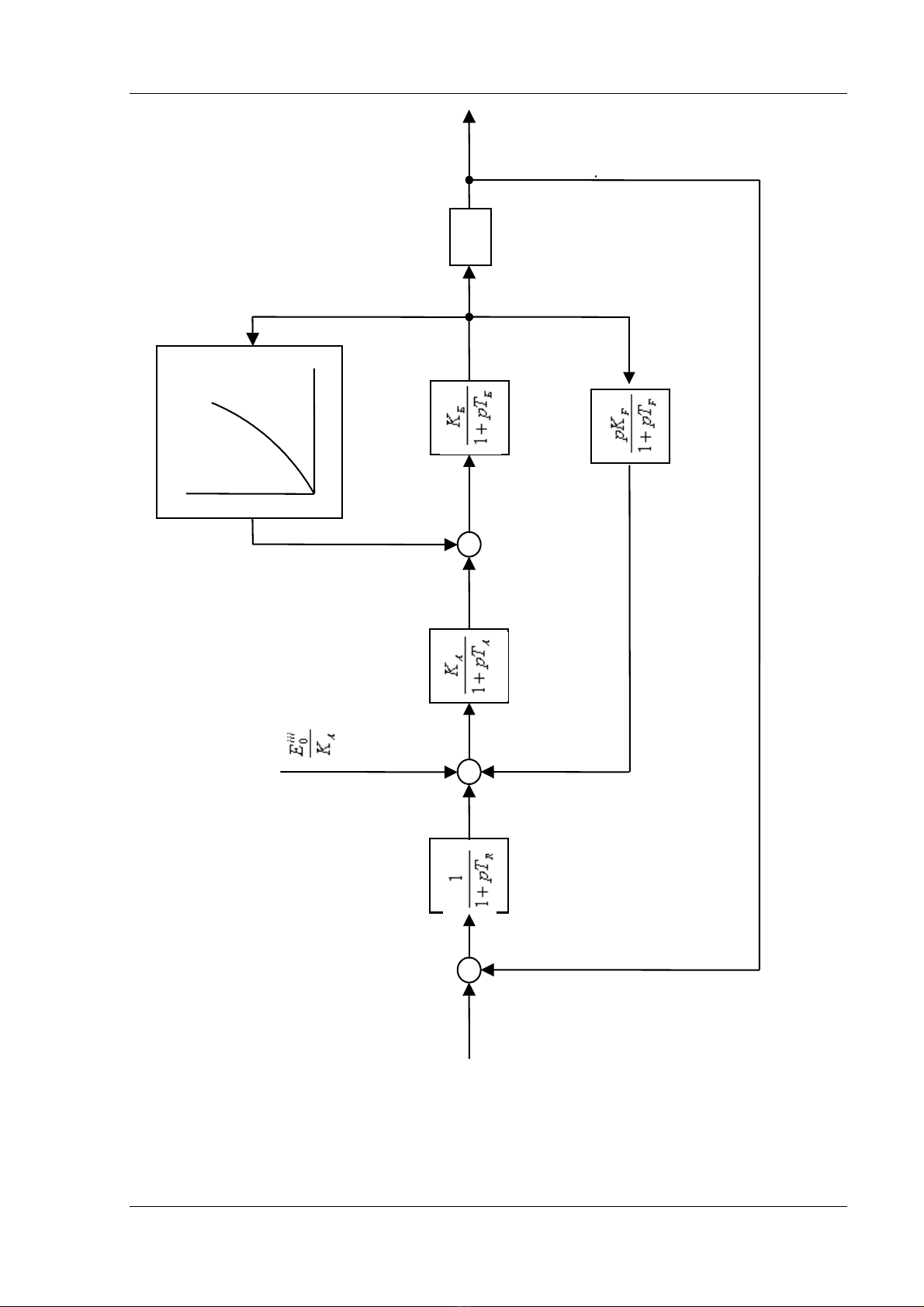
cuía hãû thäúng âiãøn khiãøn bäü kêch tæì âæåüc trçnh baìy trãn hçnh 8.7. Âáy laì 1 trong nhæîng
âiãöu kiãûn quan troüng cuía hãû thäúng âiãöu khiãøn bäü kêch tæì. Sæû âàûc træng naìy bao gäöm
nhæîng chæïc nàng chuyãøn âäøi âãø mä taí bäü âiãöu chènh, bäü khuãúch âaûi, bäü kêch tæì vaì vuìng
äøn âënh. Vuìng äøn âënh phaíi âæåüc âiãöu chènh tæång æïng âãø loaûi træì âi nhæîng dao âäüng
khäng mong muäún vaì sæû væåüt quaï âiãûn aïp âiãöu chènh. Nhæîng phæång trçnh vi phán liãn
quan âãún nhæîng biãún säú âáöu vaìo, âáöu ra cuía bäü âiãöu chènh, bäü khuãúch âaûi, bäü kêch tæì vaì
vuìng äøn âënh mäüt caïch láön læåüt laì:
()
v
tS
R
v
EEE
Tdt
dE −−= 1
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛−+= iiiiv
A
iii
v
A
A
iii
EE
K
E
EK
Tdt
dE 0
1 (8.14)
()
fdE
ii
A
df EKE
Tdt
dE −= 1
⎭
⎬
⎫
⎩
⎨
⎧−= iv
fd
F
F
iv
E
dt
dE
K
Tdt
dE 1
Våïi: Es: Laì âiãûn aïp âæåüc ghi trong lëch trçnh tênh åí âån vë tæång âäúi.
ii
i
E
0: Laì âiãûn aïp láúy ra cuía bäü khuãúch âaûi trong âån vë tæång âäúi træåïc sæû nhiãùu
loaûn.
GIAÍI TÊCH MAÛNG
Trang 129
TR: Laì hàòng säú thåìi gian cuía bäü âiãöu chènh.
KA: Laì hãû säú khuyãúch âaûi cuía bäü khuãúch âaûi.
TA: Laì hàòng säú thåìi gian cuía bäü khuyãúch âaûi.
K
E: Laì hãû säú khuyãúch âaûi cuía bäü kêch tæì.
T
E: Laì hàòng säú thåìi gian cuía bäü kêch tæì.
Es
+ -
Ev
Eiv
+
+
-
Eiii
Evi
Eii
Evi
E
t
Giåïi haûn âáöu ra giæîa
Eiiimax vaì Eiiimin
Bäü biãún âäøi Bäü ü khãúch âaûi Bäü kêch tæì
Vuìng äøn âënh
Maïy phaït
E
t
Efd
Efd
Hçnh 8.7 : Så âäö khäúi biãøu diãùn hãû thäúng âiãöu khiãøn kêch tæì
+
-
GIAÍI TÊCH MAÛNG
Trang 130
K
F: Laì hãû säú khuãúch âaûi cuía voìng äøn âënh
T
F: Laì hàòng säú thåìi gian cuía voìng äøn âënh.
Vaì caïc biãún säú trung gian âæåüc âënh roî båíi Eii, Eiii, Eiv, Ev vaì Evi . Biãún säú trung gian Eii
laì:
E
ii = Eiii - Evi
Maì Evi tæång âæång våïi aính hæåíng cuía sæû khæí tæì do sæû baío hoìa trong bäü kêch tæì. Âiãöu
naìy âæåüc xaïc âënh tæì
E
vi = AtBEfd
ÅÍ âáy A, B laì caïc hàòng säú dæûa vaìo âàûc tênh baío hoìa cuía bäü kêch tæì.
Âãø tênh âãún caïc aính hæåíng cuía hãû thäúng âiãöu khiãøn kêch tæì, thç caïc phæång trçnh (8.14)
âæåüc giaíi âäöng thåìi våïi caïc phæång trçnh (8.12) mä taí maïy âiãûn.
Aính hæåíng cuía sæû âiãöu chènh täúc âäü trong thåìi gian quaï trçnh quaï âäü coï thãø âæåüc âæa
vaìo tênh toaïn bàòng caïch sæí duûng âàûc âiãøm âaî âæåüc âån giaín hoïa cuía hãû thäúng âiãöu
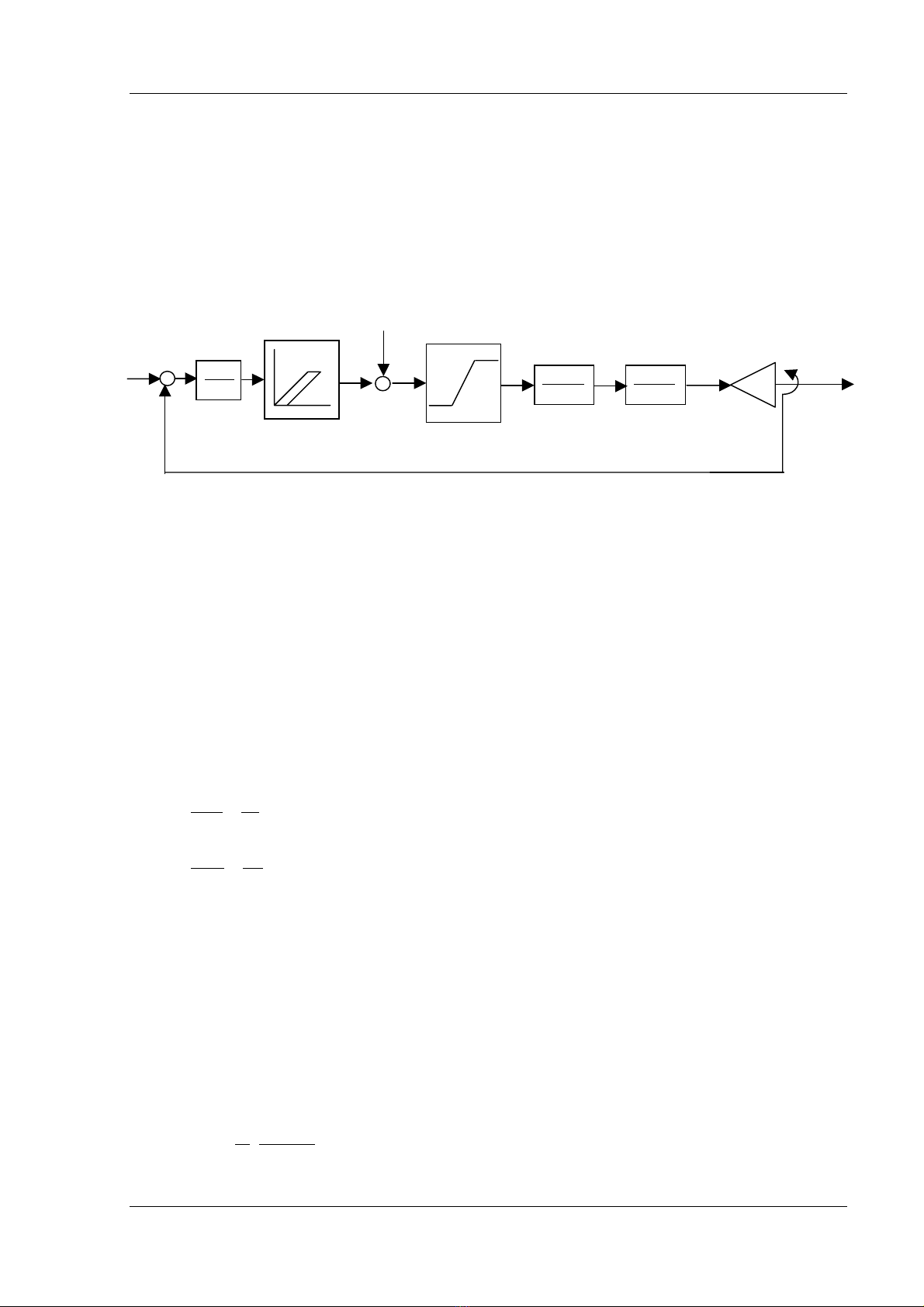
khiãøn van âiãöu chènh biãøu diãùn trãn hçnh (8.8). Âàûc træng naìy bao gäöm haìm truyãön mä
taí hãû thäúng xæí lyï håi våïi hàòng säú thåìi gian khäng âäøi Ts vaì haìm truyãön mä taí hãû thäúng
âiãöu khiãøn våïi hàòng säú thåìi gian khäng âäøi Te. Caïc phæång trçnh vi phán liãn quan âãún
caïc biãún säú âáöu vaìo vaì âáöu ra cuía haìm truyãön mäüt caïch láön læåüt laì.
)(
1
m
i
m
s
mPP
Tdt
d
P
−=
)(
1i
m
ii
m
c
i
mPP
Tdt
d
P
−= (8.15)
Trong âoï: Pm laì cäng suáút cå vaì caïc biãún säú trung gian âæåüc âënh roî båíi Pim, Piim, Piiim,
vaì Pivm. Caïc biãún säú Piim, Piiim liãn quan nhæ sau:
P
iim = 0 Piiim ≤ 0
P
iim = Piiim 0 < Piiim < Pmax
P
im = Pmax P
iii ≥ Pmax
Våïi Pmax: Laì dung læåüng cæûc âaûi cuía tua bin. Biãún säú trung gian Piiim laì:
P
iiim = Pm(0) - Pivm
Trong âoï: Pm(0): Laì cäng suáút cå ban âáöu. Biãún säú trung gian Pivm laì:
)
2
(
10
T
iv
mDB
fR
P±
−
=
π
ω
ω
fR
π
2
1
c
pT+1
1
s
pT+1
1
+ -
Vuìng chãút
Pmiv
Piiim
Pm(0)
-
+
Giåïi haûn
0
P(max) Piim
Hãû thäúng
âiãöu khiãøn Hãû thäúng
håi
Tua bin
Pm
Pim
Hçnh 8.8 : Så âäö khäúi âäúi våïi sæû biãøu diãùn âån giaín hoïa cuía hãû thäúng âiãöu chènh täúc âäü
ω
ω0
GIAÍI TÊCH MAÛNG
Trang 131
ÅÍ âáy R laì sæû âiãöu chènh täúc âäü trong âån vë tæång âäúi vaì DBT laì sæû dëch chuyãøn
cuía vuìng chãút, âoï laì sæû thay âäøi täúc âäü cáön thiãút âãø væåüt qua vuìng chãút cuía hãû thäúng van
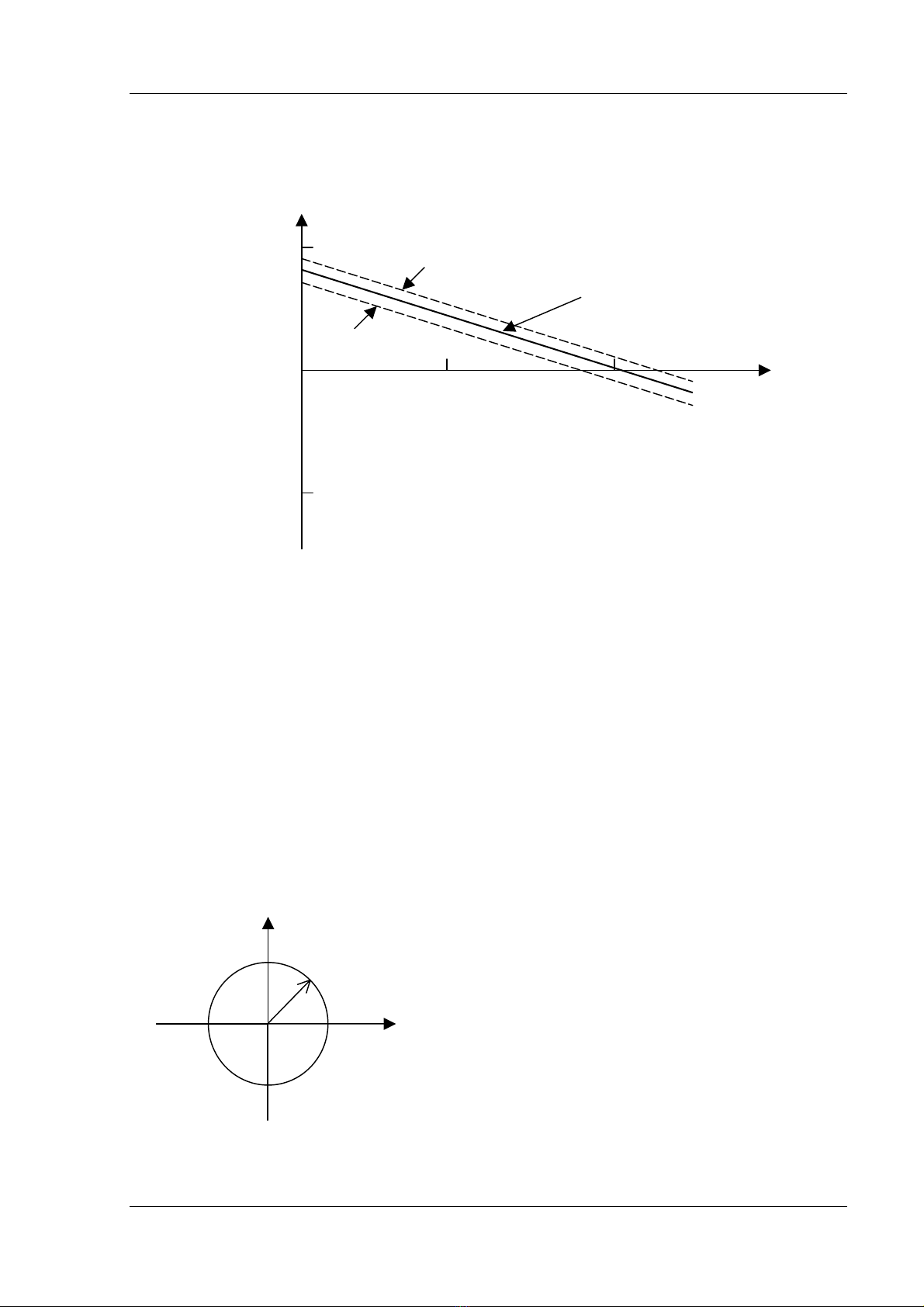
âiãöu chènh. Mäüt âàûc tênh tiãu biãøu cuía van âiãöu chènh âæåüc trçnh baìy trong hçnh 8.9.
Phæång trçnh (8.15) âæåüc giaíi âäöng thåìi våïi phæång trçnh (8.12) nãúu nhæîng aính
hæåíng cuía hãû thäúng âiãöu khiãøn van âiãöu chènh âæåüc tênh âãún.
8.7. RÅLE KHOAÍNG CAÏCH.
Sæû phäúi håüp trong kãú hoaûch phaït âiãûn, truyãön taíi âiãûn vaì viãûc thiãút kãú hãû thäúng
baío vãû råle coï hiãûu quaí laì khäng thãø thiãúu âæåüc âäúi våïi âàûc træng âäü tin cáûy cuía hãû
thäúng âiãûn. Muûc âêch chênh cuía råle laì baío vãû hãû thäúng âiãûn khoíi nhæîng aính hæåíng cuía
sæû cäú bàòng sæû khåíi âáöu váûn haình càõt maûch âãø loaûi âi nhæîng thiãút bë hæ hoíng. Viãûc thiãút
kãú hãû thäúng baío vãû råle phaíi âaím baío váûn haình choün loüc, âãø khäng càõt nháöm thiãút bë
khaïc laìm tàng thãm mæïc âäü tráöm troüng cuía sæû nhiãùu loaûn vaì noï phaíi âaím baío thiãút bë hæ
hoíng âæåüc càõt ra nhanh choïng (këp thåìi) âãø giaím âi aính hæåíng cuía sæû cäú. Hån næîa, hãû
thäúng råle phaíi khäng giåïi haûn khaí nàng thiãút kãú cuía sæû phaït âiãûn vaì thiãút bë truyãön taíi.
Mäüt loaûi råle quan troüng âæåüc sæí duûng âäúi våïi viãûc baío vãû âæåìng dáy truyãön taíi cao aïp
laì råle khoaíng caïch. Råle naìy âaïp æïng våïi tè säú âiãûn aïp vaì doìng âiãûn âo âæåüc maì coï thãø
0,5 1,0
1,05
Âiãöu chènh täúc âäü = - 0,04
Vuìng chãút = 0,0006
1,00
0,95
Täúc âäü âënh mæïc trong âå
n
vë tæång âäúi
Phuû taíi âënh mæïc trong âån vë
tæång âäúi
Hçnh 8.9 : Âàûc tênh loaûi âiãöu chènh cäng suáút âënh mæïc taûi täúc âäü âënh mæïc
Hçnh 8.10 : Âàûc tênh váûn haình cuía råle khoaíng
caïch trãn biãøu âäö hãû truûc RX
X
Z
R
0
GIAÍI TÊCH MAÛNG
Trang 132
xem nhæ mäüt täøng tråí. Mäüt caïch thuáûn tiãûn chè ra âàûc tênh váûn haình cuía råle khoaíng
caïch laì biãøu âäö RX trãn mäüt voìng troìn âæåüc veî våïi baïn kênh bàòng täøng tråí âàût nhæ hçnh
8.10. Khi giaï trë cuía täøng tråí nháûn tháúy båíi råle råi vaìo trong âæåìng troìn thç råle seî taïc
âäüng. Âãø dæû phoìng viãûc baío vãû choün loüc, råle khoaíng caïch phaíi coï 3 bäü pháûn. Âàûc tênh
taïc âäüng cuía mäùi bäü pháûn coï thãø âæåüc âiãöu chènh âäüc láûp. Hån næîa, chæïc nàng choün loüc
cuía råle khoaíng caïch âoìi hoíi khaí nàng phán biãût hæåïng. Âiãöu naìy âæåüc cung cáúp båíi
hoàûc bäü pháûn âënh hæåïng nhæ trong råle khoaíng caïch loaûi täøng tråí hoàûc laì coï sàôn trong
âàûc tênh váûn haình cuía råle, nhæ trong råle khoaíng caïch loaûi mho. Âàûc tênh váûn haình cuía
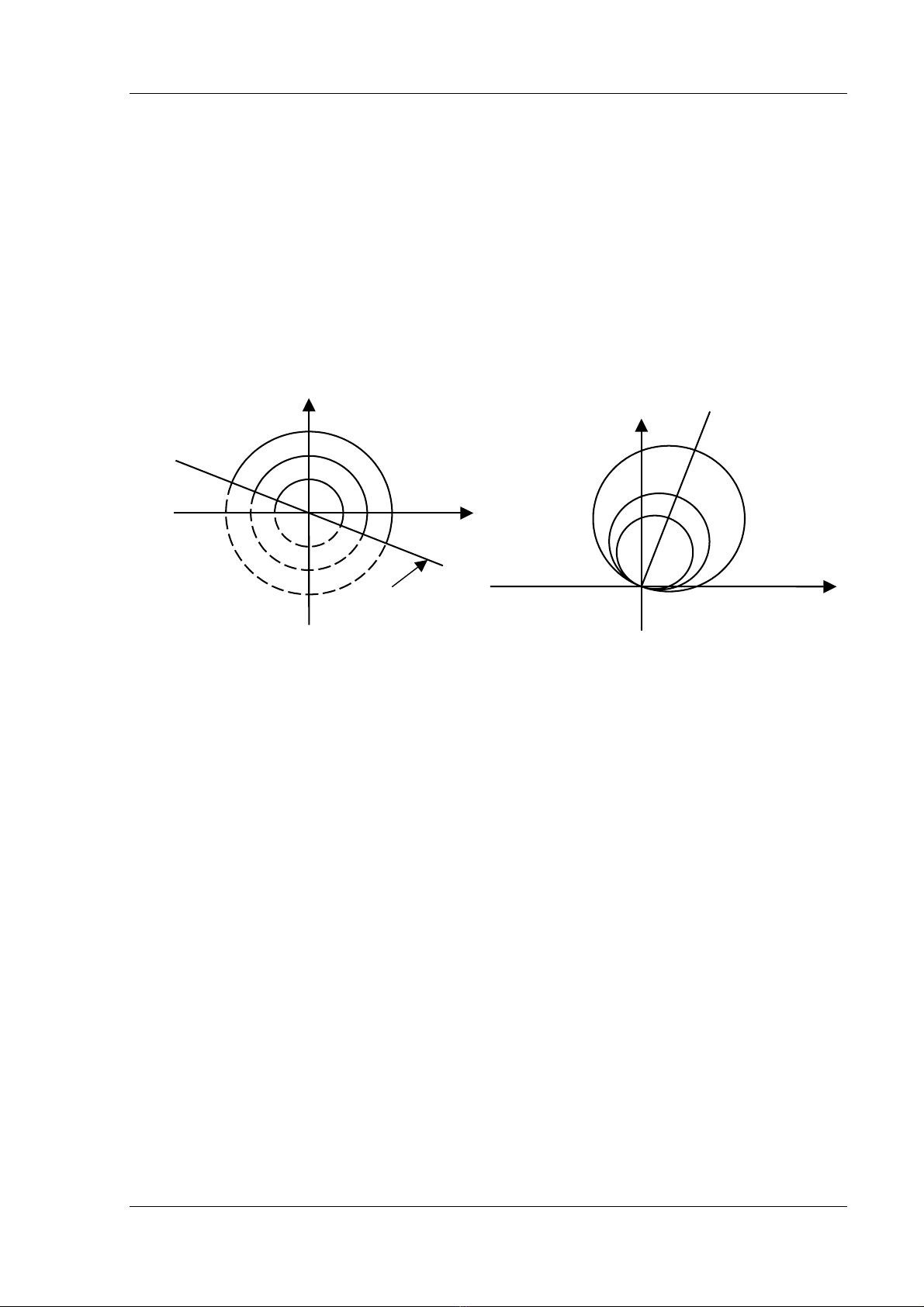
hai loaûi råle naìy âæåüc trçnh baìy trong hçnh 8.11. Caïc voìng troìn tæång æïng våïi 3 bäü pháûn
âæåüc âaïnh dáúu vuìng 1, vuìng 2 vaì vuìng 3.
Khi sæû cäú xaíy ra vaì giaï trë cuía täøng tråí âo âæåüc båíi råle råi vaìo vuìng 1 vaì trãn
âæåìng âàûc tênh cuía bäü pháûn âënh hæåïng cuía loaûi täøng tråí thç tiãúp âiãøm cuía vuìng 1 seî
âoïng vaì càõt ngàõn maûch tæïc thåìi. Trong træåìng håüp naìy táút caí 3 bäü pháûn seî khåíi âäüng båíi
vç vuìng 1 laì voìng troìn nhoí nháút. Khi tråí khaïng giaím xuäúng vaì råi vaìo vuìng 2 vaì 3 hay
vuìng 3 thç tiãúp âiãøm cuía caïc bäü pháûn tæång æïng seî âoïng vaì cung cáúp nàng læåüng cho
råle thåìi gian. Taûi mäüt thåìi âiãøm âàût theo tênh toaïn thç råle thåìi gian seî âoïng bäü thæï hai
cuía tiãúp âiãøm tæång æïng våïi vuìng 2. Nãúu bäü tiãúp âiãøm âáöu tiãn tæång æïng våïi vuìng 2
âæåüc âoïng thç maïy càõt seî âæåüc càõt. Nãúu tiãúp âiãøm vuìng 2 khäng âæåüc âoïng, thç täøng tråí
âo âæåüc båíi råle khäng råi vaìo vuìng 2, khi âoï råle thåìi gian sau thåìi gian chènh âënh seî
âoïng bäü tiãúp âiãøm thæï 2 tæång æïng våïi vuìng 3. Nãúu bäü tiãúp âiãøm âáöu tiãn tæång æïng våïi
vuìng 3 âæåüc âoïng thç khi âoï maïy càõt seî âæåüc càõt. Thåìi gian trãù âäúi våïi vuìng 2 vaì 3 coï
thãø âæåüc âàût âäüc láûp. Vuìng 1 vaì 2 cung cáúp baío vãû âoaûn âáöu tiãn âäúi våïi pháön âæåìng
dáy truyãön taíi, ngæåüc laûi vuìng 2 vaì 3 cung cáúp sæû baío vãû âoaûn sau, trong træåìng håüp hæ
hoíng nhæîng råle hoàûc laì ngàõn maûch cuía nhæîng thiãút bë liãn håüp, luïc naìy váùn váûn haình
håüp lyï.
Trong suäút sæû nhiãùu loaûn cuía hãû thäúng vaì sau khi taïc âäüng cuía bäü ngàõt váûn haình
âãø âi càõt thiãút bë sæû cäú, sæû dao âäüng cäng suáút seî xaíy ra trong hãû thäúng truyãön taíi cho
Hçnh 8.11 : Âàûc tênh váûn haình cuía råle khoaíng caïch
(a) Loaûi täøng tråí; (b) Loaûi mho
R
Âàûc tênh cuía bäü
pháûn chènh
ï
(a)
Vuìng 3
Vuìng
2
Vuìng
1
0
X
R
(b)
Vuìng 3
Vuìng 2
Vuìng
1
0