56
)()(1
1
)]()(1[)(
)(
)]()(1[
)()()()(1
2
sHsG
sHsGsG
sG
sHsG
sHsGsHsG
S
+
=
+
⋅
+
−
+
=
(4.12)
Chúng ta lại thấy một lần nữa là độ nhạy của hệ thống đối với sự biến thiên của
quá trình được điều khiển sẽ càng nhỏ khi tích G(s)H(s) càng lớn.
Sự biến thiên của phần tử phản hồi H(s) cũng gây ra thay đổi của tín hiệu ra.
Độ nhạy của hệ thống đối với sự biến thiên của phần tử phản hồi được định nghĩa
như sau:
)(
)(
sT
sH
H
T
SH⋅
∂
∂
= (4.13)
Từ (4.9) và (4.13), chúng ta thu được:
)()(1
)()(
)]()(1[)(
)(
)]()(1[
)(
2
2
sHsG
sHsG
sHsGsG
sH
sHsG
sG
SH+
−
=
+
⋅
+
−
= (4.14)
Trái với trường hợp trước, ở đây SH sẽ xấp xỉ −1 khi G(s)H(s) >> 1. Điều đó có
nghĩa là, đối với hệ thống điều khiển phản hồi việc sử dụng những bộ phận phản
hồi có độ tin cậy cao, tức là luôn giữ được các tham số không bị biến đổi theo sự
thay đổi của môi trường, là điều vô cùng quan trọng.
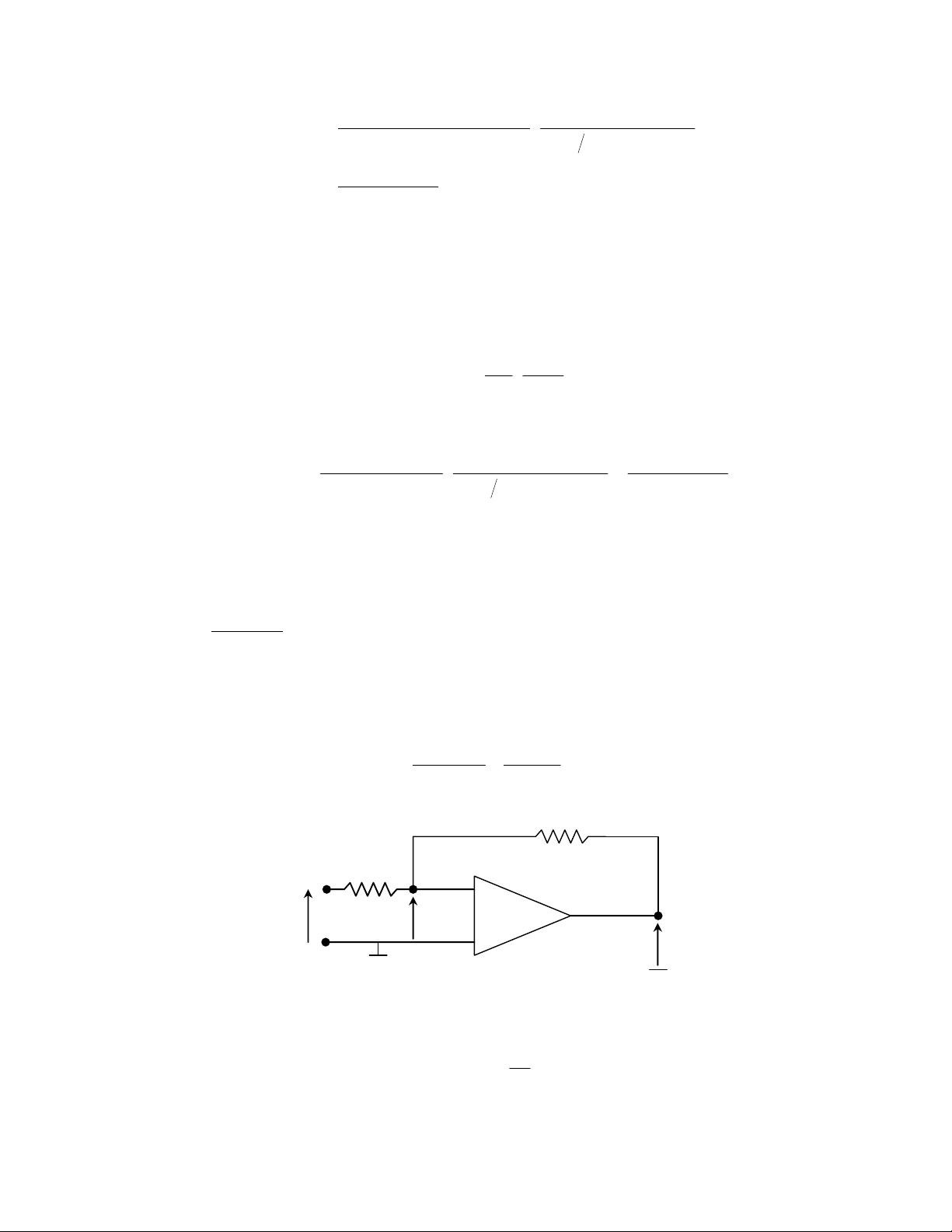
Ví dụ 4.1
Một mạch khuyếch đại đảo sử dụng khuyếch đại thuật toán được biểu diễn trong
Hình 4.2. Hệ số khuyếch đại của khuyếch đại thuật toán là A ≥ 104. Do trở kháng
của khuyếch đại thuật toán rất lớn, dòng điện đi vào bộ khuyếch đại có thể coi là
không đáng kể. Vì vậy chúng ta thiết lập được phương trình sau:
0
2
0
1
vào =
−
+
−
R
vv
R
vv nn (4.15)
v0
vvào vn
−
+
A
+
−
R1
R2
Hình 4.2. Mạch khuyếch đại đảo
Hiệu điện thế đầu ra của khuyếch đại thuật toán v0 = Avn, vì vậy:
A
v
vn0
= (4.16)
Thay (4.16) vào (4.15):
57
0
2
0
2
0
1
vào
1
0=−+− R
v
AR
v
R
v
AR
v (4.17)
hay:
121
vào2
0ARRR
vAR
v−+
= (4.18)
Hàm chuyển của hệ thống:
AKK
A
ARRR
AR
v
v
T−+
=
−+
== 1
121
2
vào
0 (4.19)
ở đó K = R1/R2. Độ nhạy của hệ thống đối với sự biến thiên của hệ số khuyếch
đại A được tính như sau:
AKK
K
AKKA
A
AKK
KAAKK
T
A
A
T
SA
−
+
+
=
−+
⋅
−+
−−−+
=
⋅
∂
∂
=
1
1
)1(
)1(
)(1
2 (4.20)
Độ nhạy của hệ thống đối với sự biến thiên của hệ số K được tính như sau:
AKK
KAK
AKKA
K
AKK
AA
T
K
K
T
SK−+
−
=
−+
⋅
−+
−
−
=⋅
∂
∂
=1)1(
)1(
)1(
2 (4.21)
Cho A = 104 và K = 0,1, chúng ta tính được SA ≅ −10−3 và SK ≅ −1. Như vậy, tín
hiệu ra của mạch khuyếch đại đảo chịu ảnh hưởng rất ít từ sự biến thiên của hệ số
khuyếch đại A của khuyếch đại thuật toán, nhưng lại bị tác động rất nhiều khi hệ
số K biến thiên.
4.3. Điều khiển đáp ứng nhất thời
Đáp ứng nhất thời (transient response) là đáp ứng của hệ thống trong một
khoảng thời gian ngắn khi xuất hiện một sự thay đổi đột ngột trong tín hiệu vào,
trước khi đạt được trạng thái thường trực. Bởi vì mục đích của hệ thống điều
khiển là tạo ra một đáp ứng được mong muốn, đáp ứng nhất thời của hệ thống
thường phải được điều chỉnh cho tới khi thỏa mãn được yêu cầu. Trong các hệ
thống điều khiển vòng hở, nếu đáp ứng của hệ thống không được như mong
muốn, quá trình G(s) sẽ cần phải được thay thế bằng quá trình khác phù hợp hơn.
Trái lại, đáp ứng của hệ thống vòng kín có thể điều chỉnh được bằng cách điều
chỉnh các tham số của vòng phản hồi. Một cách khác nữa để làm thay đổi đáp
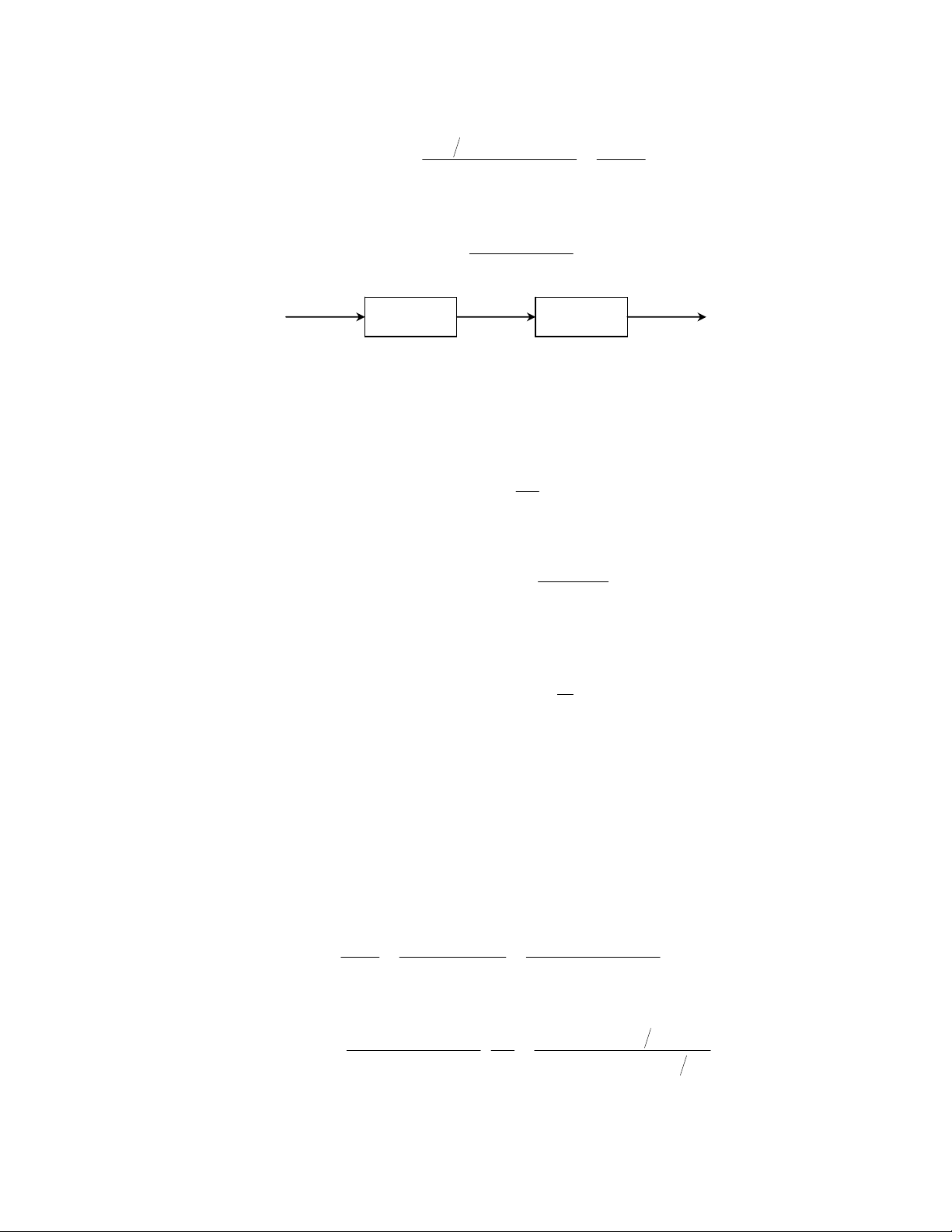
ứng của hệ thống là nối vào trước quá trình một bộ lọc có hàm chuyển là G1(s)
(Hình 4.3). Khi đó, đáp ứng của hệ thống có thể điều chỉnh được bằng việc điều
chỉnh G1(s).
Để làm ví dụ, xem xét một hệ thống điều khiển tốc độ một động cơ một chiều
điều khiển bởi phần ứng với hàm chuyển là G(s) =
Ω
(s)/Va(s). Từ công thức hàm
58
chuyển (2.62) của động cơ điều khiển bởi phần ứng, chúng ta có:
1)1(
)(
)(
1
1
1+
=
+
+
=s
K
ss
KKfRK
ssG mbam
ττ
(4.22)
ở đó:
mba
m
KKfR
K
K+
=
1 (4.23)
G1(s) G(s)
R(s) C(s)
Hình 4.3. Sử dụng bộ lọc để điều chỉnh đáp ứng
Để thay đổi tốc độ của động cơ, phát một tín hiệu vào r(t) là một hàm nhảy bậc
có dạng r = kE, ở đó E là hiệu điện thế của nguồn cung và k là một tham số có
thể điều chỉnh được bằng một biến trở. Biến đổi Laplace của r(t):
s
kE
sR =)( (4.24)
Tính
Ω
(s):
)1(
)()()(
1
1
+
== ss
EkK
sRsGsΩ
τ
(4.25)
Lấy biến đổi Laplace nghịch của
Ω
(s), chúng ta có được giá trị biến đổi tốc độ
nhất thời của động cơ:
)1()( 1
1
1
t
eEkKt
τ
ω
−
−= (4.26)
Nếu đáp ứng nhất thời này quá chậm, cách thực tế nhất là thay động cơ bằng một
cơ khác để giảm hệ số thời gian
τ
1. Tuy nhiên, do hệ số này phụ thuộc nhiều vào
quán tính của tải trọng, việc thay động cơ có thể cũng không giúp được gì nhiều.
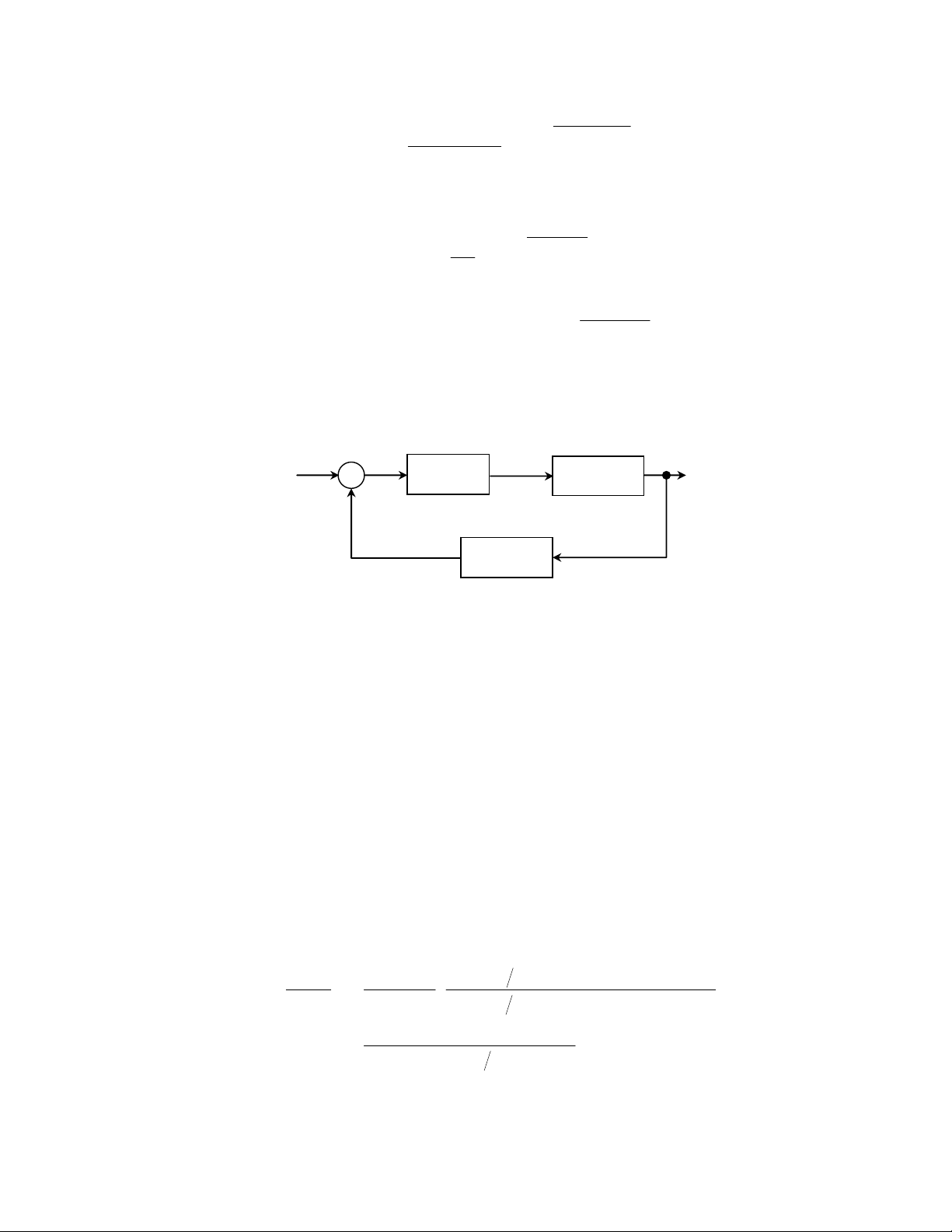
Chúng ta có thể dùng một hệ thống điều khiển vòng kín để điều khiển tốc độ
của động cơ nói trên bằng cách sử dụng một tốc độ kế có hàm chuyển là Kt để
sinh ra một tín hiệu tỷ lệ với tốc độ của động cơ (Hình 4.4). Tín hiệu sai khác
được khuyếch đại với một hệ số là Ka để sinh ra tín hiệu vào va(t) điều khiển
động cơ. Hàm chuyển của toàn bộ hệ thống vòng kín là:
11
1
1)(1
)(
)(
)(
KKKs
KK
sGKK
sGK
sR
sΩ
ta
a
ta
a
++
=
+
=
τ
(4.27)
Thay (4.24) vào (4.27):
])1([1
)(
11
11
11
1
τ
τ
τ
KKKss
kEKK
s
kE
KKKs
KK
sΩ
ta
a
ta
a
++
=⋅
++
= (4.28)
Lấy biến đổi Laplace nghịch của (4.28):
59
)1(
1
)( 1
1
1
1
1t
KKK
ta
a
ta
e
KKK
kEKK
t
τ
ω
+
−
−
+
= (4.29)
Vì KaKtK1 >> 1, chúng ta có thể lấy xấp xỉ:
)1()( 1
1t
KKK
t
ta
e
K
kE
t
τ
ω
−
−≅ (4.30)
Hệ số thời gian của hệ thống vòng kín này là
1
1
KKK ta
c
τ
τ
=. Cách dễ dàng nhất
để tăng tốc độ đáp ứng của hệ thống là tăng hệ số khuyếch đại Ka. Tuy nhiên, Ka
lớn nghĩa là hiệu điện thế vào va(t) của động cơ sẽ lớn. Vì vậy trong hệ thống
vòng kín người ta thường phải dùng động cơ lớn hơn so với hệ thống vòng hở để
tránh hiện tượng quá áp cho động cơ.
G(s)
R(s)
Ω
(s)
Hình 4.4. Hệ thống điều khiển tốc độ vòng kín
K
a
K
t
_
+ V
a
(s)
4.4. Tín hiệu nhiễu trong hệ thống điều khiển phản hồi
Hiệu ứng quan trọng thứ ba của phản hồi trong một hệ thống điều khiển là sự
điều khiển và loại trừ một phần ảnh hưởng của tín hiệu nhiễu. Một tín hiệu nhiễu
(disturbance signal) là tín hiệu không được mong muốn gây ảnh hưởng đến tín
hiệu ra của hệ thống, làm tín hiệu ra của hệ thống bị sai lệch. Các bộ khuyếch đại
điện tử có nhiễu sinh ra từ bên trong các mạch tích hợp hay transitor. Anten radar
thường bị nhiễu gây ra bởi những cơn gió mạnh. Nhiều hệ thống phát ra những
tín hiệu bị biến dạng gây ra bởi các phần tử phi tuyến. Một trong những điểm ưu
việt của các hệ thống phản hồi là khả năng làm giảm bớt ảnh hưởng của nhiễu.
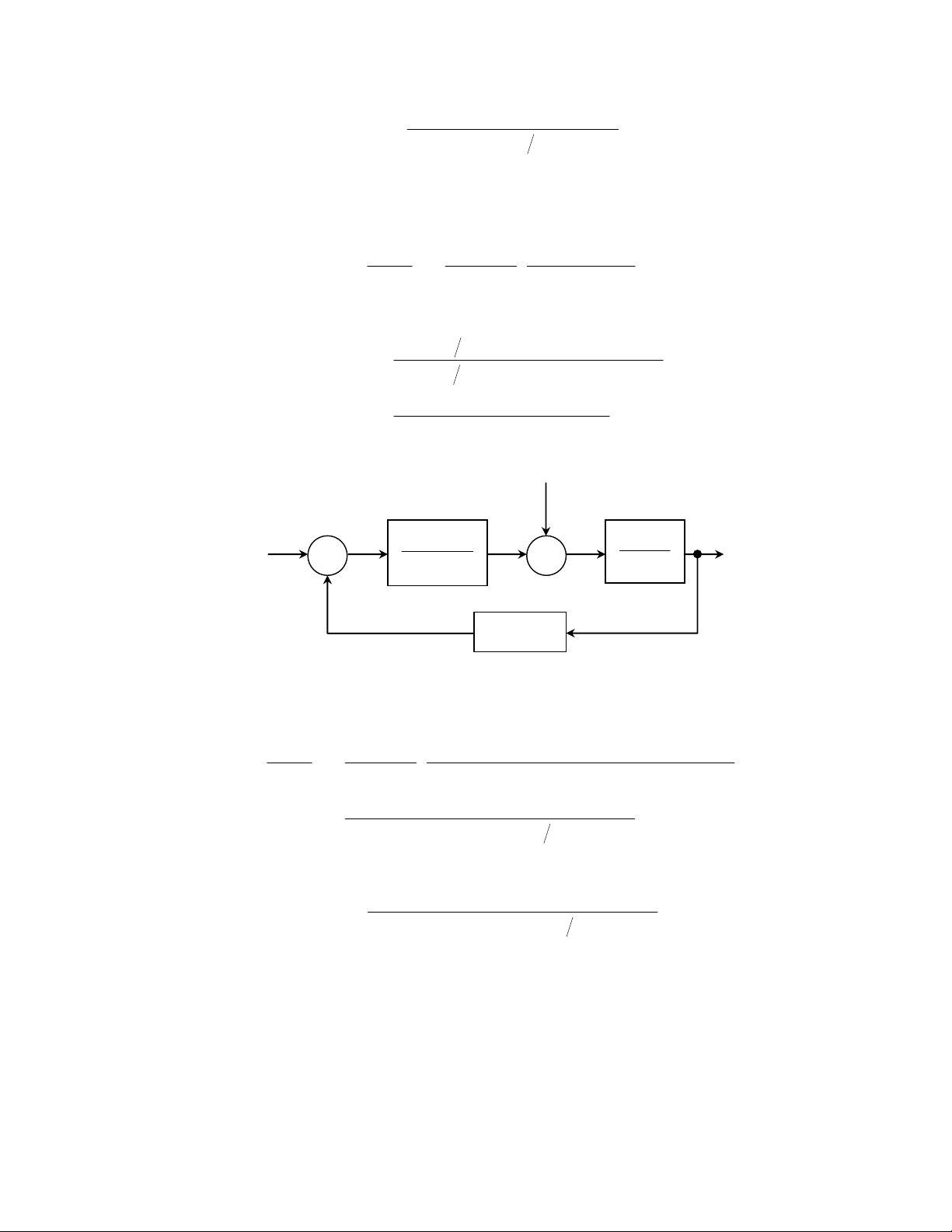
Để làm ví dụ, xem xét hệ thống điều khiển vận tốc của động cơ một chiều
điều khiển bởi phần ứng, có sơ đồ khối được biểu diễn trong Hình 4.5. Td(s) là
thành phần của mômen quay do động cơ sinh ra bởi tác động của nhiễu. Áp dụng
các kỹ thuật biến sơ đồ khối, chúng ta tính được hàm chuyển của hệ thống đối
với tín hiệu nhiễu Td(s):
)(
1
)]/(1][)([1
)]/(1][)([
)(
)(
sLRKKfJs
KfJssLRK
fJssLRK
K
sLR
sT
sΩ
aabm
baam
aam
m
aa
d
+++
−=
+++
+
+
⋅
+
−=
(4.31)
Thay đổi của vận tốc gây ra do nhiễu là:
60
)(
)(
1
)( sT
sLRKKfJs
sΩd
aabm +++
−= (4.32)
Tiếp theo, xem xét hệ thống điều khiển vận tốc vòng kín như trong Hình 4.4,
với G(s) là hệ thống vòng hở ở trên. Áp dụng các kỹ thuật biến sơ đồ khối, chúng
ta tính được hàm chuyển của hệ thống đối với tín hiệu nhiễu Td(s):
ta
a
ma
aa
dKsGK
sGK
KK
sLR
sT
sΩ
)(1
)(
)(
)(
+
⋅
+
−= (4.33)
ở đó:
bmaa
m
baam
aam
KKfJssLR
K
KfJssLRK
fJssLRK
sG
+++
=
+++
+
+
=
))((
)]/(1][)([1
)]/(1][)([
)(
(4.34)
+
Tm(s)
sLR
K
aa
m
+
Va(s) TL(s)
Td(s)
fJs +
1
Ω
(s)
Hình 4.5. Hệ thống điều khiển vận tốc vòng hở
−
+
Kb
−
Thay (4.34) vào (4.33):
)()(
1
))(()(
)(
sLRKKKKfJs
KKKKKfJssLR
KK
KK
sLR
sT
sΩ
aatabm
tmabmaa
ma
ma
aa
d
++++
−=
++++
⋅
+
−=
(4.35)
Thay đổi của vận tốc gây ra do nhiễu trong trường hợp của hệ thống vòng kín là:
)(
)()(
1
)( sT
sLRKKKKfJs
sΩd
aatabm ++++
−= (4.36)
So sánh hai công thức (4.32) và (4.36), chúng ta thấy rõ ràng là ảnh hưởng của
nhiễu tới vận tốc của động cơ giảm đi ở hệ thống vòng kín so với hệ thống vòng
hở.
Lưu đồ trong Hình 4.6 biểu diễn trường hợp được tổng quát từ ví dụ trên. Sử
dụng quy tắc vòng của Mason, chúng ta tính được ảnh hưởng của tín hiệu nhiễu
Td(s) tới tín hiệu ra như sau: