
I. Mô hình đ cao s - DEM (Digital Elevation Model)ộ ố
II.1/ Gi i thi u chung:ớ ệ
Khác v i các đn v s d ng đt, phân lo i đt và đa ch t, đ caoớ ơ ị ử ụ ấ ạ ấ ị ấ ộ
đa hình có xu h ng bi n đi liên t c nên không th bi u di n chúngị ướ ế ổ ụ ể ể ễ
b ng b n đ chuyên d ng thông th ng. T t nhiên trong đa hình t n t iằ ả ồ ụ ườ ấ ị ồ ạ
nh ng vùng thay đi đ cao đt ng t nh v c sâu, khe núi nh ng ph nữ ổ ộ ộ ộ ư ự ư ầ
l n ch là s thay đi c c b .ớ ỉ ự ổ ụ ộ
Thông th ng thì s thay đi đ cao đa hình đc th hi n b ngườ ự ổ ộ ị ượ ể ệ ằ
m t lo t đng đng m c mà các đi m trên m t đng đng m c cóộ ạ ườ ồ ứ ể ộ ườ ồ ứ
cùng m t giá tr đ cao. Các đng này là các đng cong kép kín màộ ị ộ ườ ườ
trong GIS ng i ta g i là các polygons. B ng ph ng pháp này thì y u tườ ọ ằ ươ ế ố
đa hình cũng đc th hi n và l u tr trong GIS nh trong các b n đị ượ ể ệ ư ữ ư ả ồ
chuyên dùng khác. Tuy v y ph ng pháp bi u th đó ch a ph i là t i uậ ươ ể ị ư ả ố ư
khi s d ng ph ng pháp s đ phân tích và đ mô hình hóa. Ng i taử ụ ươ ố ể ể ườ
c n m t ph ng pháp t t h n đ hi n th và phân tích lo i d li u thayầ ộ ươ ố ơ ẻ ể ị ạ ữ ệ
đi liên t c (t ng t nh s đo đ cao đa hình) và ph ng pháp đó làổ ụ ươ ự ư ố ộ ị ươ
mô hình s đ cao.ố ộ
B t k s bi u th b ng s s thay đi liên t c c a đ cao trongấ ỳ ự ể ị ằ ố ự ổ ụ ủ ộ
không gian đu đc g i là mô hình s đ cao (Digital Elevation Model,ề ượ ọ ố ộ
DEM). Nó có th là đ cao tuy t đi c a các đi m trên b m t qu đt,ể ộ ệ ố ủ ể ề ặ ả ấ
đ cao c a các t ng đt, ho c c a m c n c ng m. DEM còn nhi u tênộ ủ ầ ấ ặ ủ ự ướ ầ ề
g i khác trong ti ng Anh nh là Digital Terrain Model (DTM), Digitalọ ế ư
Terrain Data (TDD) và Digital Terrain Elevation Data (DTED). Ngoài ngứ
d ng đ bi u th đa hình, DEM còn có th đc ng d ng đ th hi n sụ ể ể ị ị ể ượ ứ ụ ể ể ệ ự
thay đi liên t c trong kho ng không hai chi u c a b t k thông s môiổ ụ ả ề ủ ấ ỳ ố
tr ng khác nào.ườ
S c n thi t c a DEM, mô hình s đ cao có vô vàn ng d ng trongự ầ ế ủ ố ộ ứ ụ
th c ti n, đc bi t ph bi n là nh ng ng d ng sau:ự ễ ặ ệ ổ ế ữ ứ ụ
1. L u tr d li u b n đ s đa hình trong các c s d li uư ữ ữ ệ ả ồ ố ị ơ ở ữ ệ
(CSDL) qu c gia.ố
2. Gi i quy t tính toán đào l p đt trong thi t k đng và các dả ế ắ ấ ế ế ườ ự
án k thu t công chánh khác.ỹ ậ

3. Bi u th ba chi u tr c quan đi u ki n đa hình có m c đích quânể ị ề ự ề ệ ị ụ
s (thi t k h th ng đn đo, hu n luy n phi công) và cho m cự ế ế ệ ố ạ ạ ấ ệ ụ
đích thi t k và quy ho ch c nh quan (ki n trúc c nh quan)ế ế ạ ả ế ả
4. Phân tích t m quan sát xuyên đa hình (t ng t dùng cho m cầ ị ươ ự ụ
đích quân s và thi t k c nh quan)ự ế ế ả
5. Thi t k xác đnh v trí cho đng giao thông và cho đp n c.ế ế ị ị ườ ậ ướ
6. Phân tích th ng kê và so sánh các lo i đa hìnhố ạ ị
7. Tính toán và thành l p b n đ đ d c, b n đ h ng d c, b nậ ả ồ ộ ố ả ồ ướ ố ả
đ hình d ng mái d c đ t đó thành l p nh đa hình tr c quanồ ạ ố ể ừ ậ ả ị ự
có hình bóng ( ng d ng trong nghiên c u t ng đa ch t hay dứ ụ ứ ầ ị ấ ự
báo kh năng xói mòn đt và dòng ch y m t)ả ấ ả ặ
8. S d ng làm b n đ n n hay b n đ tích h p v i các b n đử ụ ả ồ ề ả ồ ợ ớ ả ồ
chuyên d ng nh b n đ lo i đt, lo i s d ng đt hay th mụ ư ả ồ ạ ấ ạ ử ụ ấ ả
th c v t.ự ậ
9. S d ng nh là d li u vào cho các mô hình mô ph ng c nhử ụ ư ữ ệ ỏ ả
quan và các quá trình t nhiên liên quan đn c nh quan môiự ế ả
tr ng.ườ
10.Khi thay th đ cao b ng m t trong các thông s thu c tính khácế ộ ằ ộ ố ộ
thì DEM có th bi u th tr c quan d ng m t cong cho v n để ể ị ự ạ ặ ấ ề
quãng th i gian hành trình, giá thành, dân s , m c đ ô nhi m,ờ ố ứ ộ ễ
m c n c ng m...ự ướ ầ
II.2/ Ph ng pháp bi u th DEM:ươ ể ị
S bi n đi giá tr đ cao đa hình trên m t vùng đt có th đc môự ế ổ ị ộ ị ộ ấ ể ượ
hình hóa theo nhi u cách. DEM có th đc bi u th và l u tr d i d ngề ể ượ ể ị ư ữ ướ ạ
hàm s toán h c ba chi u (ph ng trình m t ph ng) hay d i d ng cácố ọ ề ươ ặ ẳ ướ ạ
đi m ho c các đng hình nh nh li t kê b ng d i:ể ặ ườ ả ư ệ ở ả ướ
B ng 1.1 Ph ng pháp bi u th m t cong đa hìnhả ươ ể ị ặ ị
A. Ph ng pháp toán h cươ ọ
Toàn vùng Dãy Fourier
Đa th c b c b n b iứ ậ ố ộ
Chi ti tếChia vùng đng đuồ ề
Chia vùng không đng đuồ ề
B. Ph ng pháp v t thươ ậ ể Đng đng m c (đng bìnhườ ồ ứ ườ

b n đả ồ đ ngang)ộ
Đng m t c t d cườ ặ ắ ọ
Đi m (ma trân đ cao) hay m ngể ộ ạ
l i đu (Regular rectangularướ ề
grid, GRID)
Vector: M ng không đu tam giácạ ề
(Triangualr irregualar network,
TIN)
1. Ph ng pháp toán h c:ươ ọ
Ph ng pháp toán h c đ bi u th m t cong đa hình ch y u d a vàoươ ọ ể ể ị ặ ị ủ ế ự
các hàm s toán ba chi u và có kh năng mô ph ng v i đ nh n r t caoố ề ả ỏ ớ ộ ẵ ấ
các m t đa hình ph c t p. Ph ng pháp c c b chia vùng mô ph ng raặ ị ứ ạ ươ ụ ộ ỏ
thành các mi ng bé hình vuông ho c hình d ng tùy ý có di n tích t ng tế ặ ạ ệ ươ ự
nhau và đ cao c a t ng mi ng s đc c l ng d a trên đ cao cácộ ủ ừ ế ẽ ượ ướ ượ ự ộ
đi m đã quang tr c trong mi ng đó. V i m c đích b o đm s liên t cể ắ ế ớ ụ ả ả ự ụ
c a đ d c qua đng biên gi a các mi ng con thì ng i ta s d ng cácủ ộ ố ườ ữ ế ườ ử ụ
hàm s đi tr ng (weighting functions). Các hàm s x p x r i r cố ố ọ ố ấ ỉ ờ ạ
(piecewwise approximation) r t ít khi đc s d ng trong vi c thành l pấ ượ ử ụ ệ ậ
b n đ s nh ng l i r t ph bi n trong h th ng máy tính h tr thi t kả ồ ố ư ạ ấ ổ ế ệ ố ỗ ợ ế ế
(CAD, computer added design).
2. Ph ng pháp v t th b n đ:ươ ậ ể ả ồ
Ph ng pháp s d ng v t th đng đu tiên truy n th ng trong b nươ ử ụ ậ ể ườ ầ ề ố ả
đ h c đ bi u di n b m t đa hình là s d ng đng bình đ hay cònồ ọ ể ể ễ ề ặ ị ử ụ ườ ộ
g i là đng đng m c. M i đi m n m trên cùng m t đng đng m cọ ườ ồ ứ ọ ể ằ ộ ườ ồ ứ
s có cùng m t giá tr đ cao.ẽ ộ ị ộ
Ph ng pháp s d ng m t c t d c đ bi u di n đ cao đc sươ ử ụ ặ ắ ọ ể ể ễ ộ ượ ử
d ng thu n ti n đ phân tích đ d c vùng nghiên c u. Tuy nhiên, nh đãụ ậ ệ ể ộ ố ứ ư
đ c p trên, hai ph ng pháp s d ng đng trên không thu n ti n choề ậ ở ươ ử ụ ườ ậ ệ
m c đích phân tích d li u trong GIS. Vì v y ph ng pháp chung nh tụ ữ ệ ậ ươ ấ
trong h GIS là s d ng mô hình l i đu GRID (Regular Rectangularệ ử ụ ướ ề
Grid) hay l i tam giác không đu TIN (triangular Irregular Network).ướ ề
Mô hình l i đng đu hay còn g i là ma tr n đ cao đc thành l pướ ồ ề ọ ậ ộ ượ ậ
t vi c phân tích l p th nh hàng không ho c có th thông qua vi c n iừ ệ ậ ể ả ặ ể ệ ộ
suy t l i d li u quan tr c đ cao. Do máy tính có kh năng x lý maừ ướ ữ ệ ắ ộ ả ử
tr n d dàng nên d li u lo i mô hình GRID này r t ph bi n, đc sậ ễ ữ ệ ạ ấ ổ ế ượ ử

d ng cho các h GIS d ng raster. Trong mô hình raster GRID này vùng đaụ ệ ạ ị
hình đc chia thành các ô (cell) trên c s hàng và c t. M i m t ô ch aượ ơ ở ộ ỗ ộ ứ
đ cao c a đi m trung tâm c a ô. Ma tr n đ cao đc s d ng đ thànhộ ủ ể ủ ậ ộ ượ ử ụ ể
l p đng đng m c, tính toán đ d c, h ng d c và xác đnh đngậ ườ ồ ứ ộ ố ướ ố ị ườ
biên các l u v c sông.ư ự
Tuy v y, ph ng pháp l i đng đu này có các nh c đi m sau:ậ ươ ướ ồ ề ượ ể
- T n t i s l ng d li u không c n thi t t i các vùng cóồ ạ ố ượ ữ ệ ầ ế ạ
đa hình đng nh t;ị ồ ấ
- Không có kh năng thích ng đ bi u th các vùng có đaả ứ ể ể ị ị
hình ph c t p tr lúc thay đi toàn b kích th c ma tr n.ứ ạ ừ ổ ộ ướ ậ
Nh v y, l i đng đu không có kh năng bi u th các vùng đaư ậ ướ ồ ề ả ể ị ị
hình thay đi đt ng t nh các khe v c, h l i lõm và sông ngòi. H n chổ ộ ộ ư ự ố ồ ạ ế
này có th gây s nh m l n trong khi đánh giá k t qu phân tích đa hình.ể ự ầ ẫ ế ả ị
TIN đc coi là ph ng pháp thu n ti n và kinh t h n. Mô hình TINượ ươ ậ ệ ế ơ
là th hi n vector c a c u trúc đa hình, bao g m các dãy tam giác khôngể ệ ủ ấ ị ồ
đu không ph lên nhau và bao trùm toàn b b m t đa hình, m i m tề ủ ộ ề ặ ị ỗ ộ
tam giác xác đnh m t m t ph ng. TIN, theo khái ni m hình h c là t p cácị ộ ặ ẳ ệ ọ ậ
đnh n i v i nhau thành các tam giác. M i m t tam giác đc gi i h n b iỉ ố ớ ỗ ộ ượ ớ ạ ở
3 đi m đc tr ng v giá tr X, Y và Z (đ cao). Các tam giác này hìnhể ặ ư ề ị ộ
thành m t b m t 3 phía, có đ d c và h ng d c. TIN có kh năng bi uộ ề ặ ộ ố ướ ố ả ể
di n b m t liên t c t t p đi m d li u r i r c và đc coi nh t p h pễ ề ặ ụ ừ ậ ể ữ ệ ờ ạ ượ ư ậ ợ
các tam giác có các thu c tính v đ d c, di n tích và h ng. Hình IV.9ộ ề ộ ố ệ ướ
th hi n c u trúc mô hình TIN và hình IV.10 trình bày mô hình TIN trongể ệ ấ
th c t khi th ng ph i th hi n s thay đi kích th c l i theo yêu c uự ế ườ ả ể ệ ự ổ ướ ướ ầ
bi n đi c a d li u. Hình IV.11 là ví d v áp d ng TIN và k thu t tôế ổ ủ ữ ệ ụ ề ụ ỹ ậ
bóng đ th hi n đ cao đa hình m t khu v cể ể ệ ộ ị ộ ự
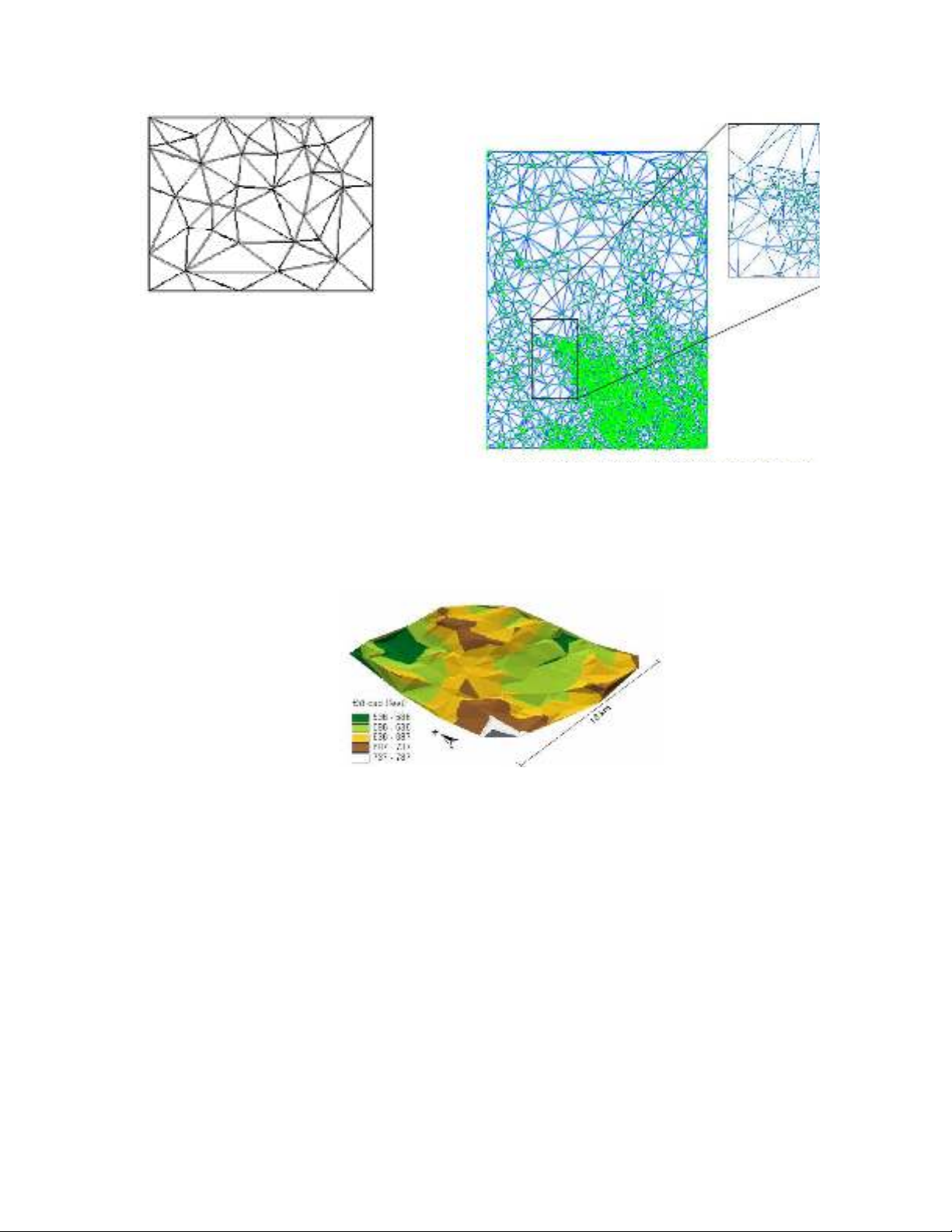
Hình IV.9: Ví d mô hìnhụ
TIN
Hình IV.10: M ng TIN v i s thay điạ ớ ự ổ
kích th c l i đc tr ngướ ướ ặ ư
Hình IV.11: ng d ng TIN đ bi u th s bi n đng đ cao đa hìnhỨ ụ ể ể ị ự ế ộ ộ ị
II.3/ Ph ng pháp xây d ng DEM:ươ ự
Ph ng pháp ch p nh l p th :ươ ụ ả ậ ể
Ph ng pháp này dùng m t d ng c ch p nh chuyên dùng đ ch pươ ộ ụ ụ ụ ả ể ụ
m t s l ng l n đi m m u v i các giá tr X, Y, Z t các nh l p th hayộ ố ượ ớ ể ẫ ớ ị ừ ả ậ ể
vi n thám; sau đó các đi m đc n i suy thành các ô vuông đng nh tễ ể ượ ộ ồ ấ
(grid). Ph ng pháp này t n th i gian và đòi h i k thu t ch p nh cao vàươ ố ờ ỏ ỹ ậ ụ ả
s đi m ki m soát ph i nhi u nên ít khi đc áp d ng.ố ể ể ả ề ượ ụ
N i suy t các đng đng m c:ộ ừ ườ ồ ứ

![PROFIBUS và mạng truyền thông: Tổng quan, ứng dụng [Năm hiện tại]](https://cdn.tailieu.vn/images/document/thumbnail/2019/20191208/camtucau99/135x160/9551575800543.jpg)




![Thiết bị công nghệ nào ngốn điện nhất? [Top thiết bị ngốn điện]](https://cdn.tailieu.vn/images/document/thumbnail/2012/20121217/bibocumi21/135x160/1315182_0610.jpg)



















