BỘ GIÁO DỤC VÀ ĐÀO TẠO
TRƯỜNG ĐẠI HỌC XÂY DỰNG HÀ NỘI
Lê Thanh Hải
PHÂN TÍCH PHI TUYẾN ỨNG XỬ TĨNH VÀ
ỔN ĐỊNH CỦA TẤM BẰNG VẬT LIỆU FGM RỖNG
Chuyên ngành: Cơ kỹ thuật
Mã số: 9520101
TÓM TẮT LUẬN ÁN TIẾN SĨ
Hà Nội - Năm 2022
Công trình được hoàn thành tại Trưng Đi hc Xây dng Hà Nội
Người hướng dẫn khoa học 1: GS. TS Trần Minh Tú - Trường Đại học
Xây dng Hà Nội
Người hướng dẫn khoa học 2: GS. TS Lê Xuân Huỳnh - Trường Đại học
Xây dng Hà Nội
Phản biện 1: GS. TSKH Nguyễn Đông Anh
Phản biện 2: GS. TS Nguyễn Tiến Chương
Phản biện 3: GS. TS Trần Ích Thịnh
Luận án sẽ được bảo vệ trước Hội đồng chấm luận án tiến sĩ cấp Trường
họp tại Trường Đại học Xây dng Hà Nội.
vào hồi ...... giờ ......', ngày ..... tháng ..... năm 2022
Có thể tìm hiểu luận án tại:
- Thư viện Quốc gia và thư viện Trường Đại học Xây dng Hà Nội.
1
MỞ ĐẦU
1. Tính cấp thiết của đề tài
Vật liệu FGM rỗng (functionally graded porous materials – FGPMs) là một trong những biến thể của vật
liệu FGM. Trong cấu trúc loại vật liệu này có chứa các lỗ rỗng với kích thước và mật độ biến thiên theo
một quy luật nhất định, như vậy các cơ tính vật liệu có thể được coi là biến đổi trơn theo tọa độ không gian
kết cấu. Là loại vật liệu nhẹ với khả năng hấp thụ năng lượng tốt, cũng như hệ số truyền nhiệt thấp, nên
chúng thường được sử dụng để chế tạo những cấu kiện chịu tải trọng động, cách âm, cách nhiệt,… Nghiên
cứu ứng xử cơ học của kết cấu tấm bằng vật liệu FGM rỗng phục vụ công tác hướng dẫn thiết kế, thi công
và bảo trì đã và đang là vấn đề có tính cấp thiết, có ý nghĩa khoa học lẫn thc tiễn.
Phân tích phi tuyến ứng xử của kết cấu tuy phức tạp, đòi hỏi những phương pháp tiếp cận với độ phức tạp về
mặt toán học cao, tuy nhiên đây vẫn là hướng nghiên cứu thu hút được s quan tâm của giới chuyên môn do
phản ánh sát hơn s làm việc thc tế của kết cấu. Trên cơ sở đó luận án la chọn đề tài: “Phân tích phi tuyến
ứng xử tĩnh và ổn định của tấm bằng vật liệu FGM rỗng”.
2. Mục tiêu nghiên cứu của luận án
Trên cơ sở lý thuyết biến dạng cắt bậc nhất và lý thuyết tấm cổ điển xây dng các hệ thức quan hệ và các
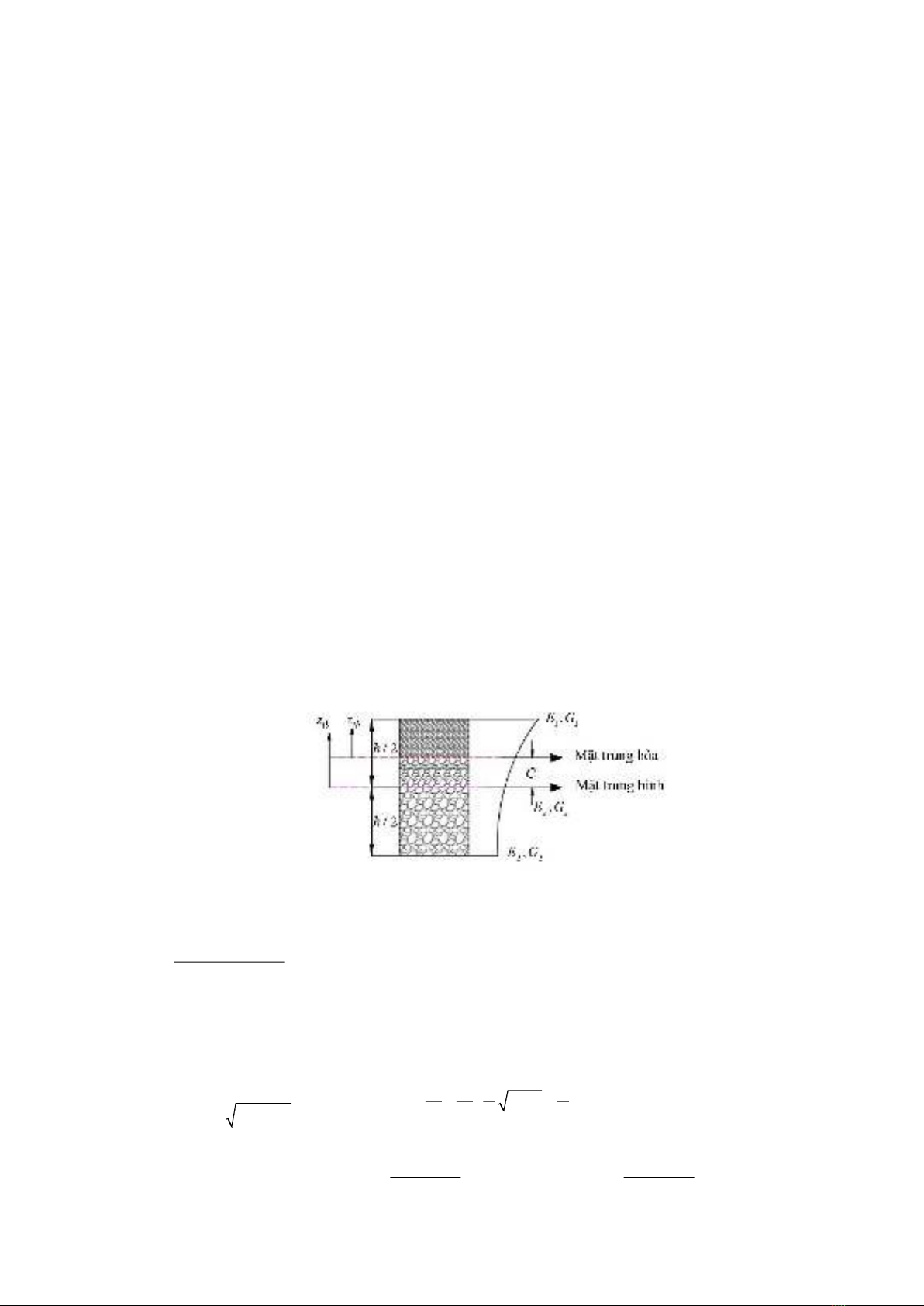
phương trình chủ đạo của tấm bằng vật liệu FGM rỗng với hệ toạ độ quy chiếu đặt trên mặt trung hoà. Tấm đặt
trên nền đàn hồi Pasternak với các điều kiện biên khác nhau, có kể đến độ không hoàn hảo hình học ban đầu và
thành phần biến dạng phi tuyến hình học von Kárman.
Thiết lập lời giải giải tích cho bài toán phân tích phi tuyến ứng xử uốn của tấm vật liệu FGM rỗng theo hai
cách tiếp cận: theo ứng suất và theo chuyển vị.
Thiết lập lời giải giải tích cho bài toán phân tích phi tuyến ổn định và sau ổn định của tấm vật liệu FGM
rỗng theo tiếp cận ứng suất.
Viết chương trình tính trên nền Matlab để khảo sát ảnh hưởng của tham số vật liệu, kích thước hình học, hệ
số nền đàn hồi, điều kiện biên và tải trọng đến độ võng, đường cong tải-mô men uốn, lc tới hạn và đường
cong sau ổn định của tấm bằng vật liệu FGM rỗng.
3. Đối tượng và phm vi nghiên cứu của luận án
Đối tượng nghiên cứu của luận án là tấm chữ nhật có chiều dày không đổi, đặt trên nền đàn hồi với các điều kiện
biên khác nhau. Vật liệu FGM rỗng, cụ thể là bọt kim loại (open-cell metal foam) với các lỗ rỗng biến đổi trơn
theo chiều dày tấm theo ba quy luật: phân bố đều, không đều đối xứng và không đều bất đối xứng được khảo sát.
Các hằng số vật liệu như vậy cũng biến đổi trơn theo ba quy luật trên, tuy nhiên để đơn giản, hệ số Poisson được
xem là không thay đổi theo chiều dày tấm.
Phạm vi nghiên cứu của luận án là: phân tích phi tuyến ứng xử uốn và ổn định của tấm FGM rỗng: xác định
độ võng, thành phần nội lc; tải trọng tới hạn và đường cong sau ổn định của tấm vật liệu FGM rỗng.
4. Phương pháp nghiên cứu
Phương pháp nghiên cứu trong luận án là nghiên cứu lý thuyết và thc nghiệm số. Trên cơ sở của lý thuyết
biến dạng cắt bậc nhất và lý thuyết tấm cổ điển, các hệ thức quan hệ phi tuyến và các phương trình chủ đạo
của tấm vật liệu FGM rỗng trên nền đàn hồi đã được thiết lập có xét đến vị trí thc của mặt trung hoà.
Chương trình tính trên nền Matlab đã được xây dng nhằm khảo sát ảnh hưởng của các tham số thiết kế
đến ứng xử phi tuyến uốn, ổn định và sau ổn định của tấm bằng vật liệu FGM rỗng với các điều kiện biên
SSSS, CCCC, SCSC.
5. Những đóng góp mới của Luận án
Luận án đã xây dng hệ thức cơ bản và các phương trình chủ đạo, để phân tích phi tuyến ứng xử tĩnh và ổn
định của tấm bằng vật liệu FGM rỗng không hoàn hảo đặt trên nền đàn hồi, có kể đến vị trí thc của mặt
trung hoà, và thành phần phi tuyến hình học von Kárman, da trên lý thuyết biến dạng cắt bậc nhất và lý
thuyết tấm cổ điển.
Thiết lập lời giải giải tích theo phương pháp ứng suất và phương pháp chuyển vị để khảo sát ứng xử phi
tuyến uốn tấm FGM rỗng. Sử dụng phương pháp Bubnov-Galerkin để thu được hệ phương trình đại số phi
tuyến xác định độ võng và thành phần nội lc của tấm hoàn hảo với các mức tải trọng và điều kiện biên
khác nhau.
Sử dụng hàm ứng suất Airy, kết hợp với phương pháp Bubnov-Galerkin, đã thiết lập được biểu thức hiển
của tải tới hạn và quan hệ tải - độ võng của tấm bằng vật liệu FGM rỗng hoàn hảo và không hoàn hảo chịu
nén trong mặt trung hòa.
Các kết quả khảo sát cho thấy ảnh hưởng rõ rệt của các tham số vật liệu (quy luật phân bố, hệ số lỗ rỗng),
nền đàn hồi, điều kiện biên, kích thước hình học đến ứng xử tĩnh và ổn định của tấm FGM rỗng. Bộ số liệu
thu được cùng các nhận xét mang tính kỹ thuật là nguồn tham khảo hữu ích cho công tác thiết kế, thi công
và bảo trì các kết cấu sử dụng vật liệu FGM rỗng trong thc tế.
2
6. Bố cục của luận án
Luận án gồm: Mở đầu, bốn chương chính, kết luận, danh mục các công trình khoa học của tác giả, tài liệu
tham khảo và phụ lục.
CHƯƠNG 1. TỔNG QUAN VẤN ĐỀ NGHIÊN CỨU
Chương này giới thiệu tóm tắt về vật liệu FGM rỗng, phương pháp chế tạo và tính chất cơ học của vật liệu, kết
cấu bằng vật liệu FGM rỗng và ứng dụng. Tổng quan tình hình nghiên cứu trong và ngoài nước về kết cấu bằng vật liệu
FGM và FGM rỗng. Qua nghiên cứu tổng quan, các nghiên cứu phân tích về kết cấu dầm và tấm bằng vật liệu FGM
rỗng (metal foam) hay bằng vật liệu FGM có chứa vi bọt rỗng (FGM with porosity) ta có thể thấy rằng còn có ít các
công trình nghiên cứu về ứng xử phi tuyến uốn, ổn định và sau ổn định của kết cấu tấm sử dụng vật liệu FGM rỗng.
Đặc biệt là chưa có phân tích, so sánh đánh giá một cách đầy đủ về hai cách tiếp cận ứng suất và chuyển vị để giải quyết
bài toán uốn, ổn định và sau ổn định của tấm FGM rỗng có kể đến tính phi tuyến hình học.
Với tiềm năng sử dụng loại vật liệu này hiện tại và trong tương lai, tác giả luận án đề xuất hướng nghiên
cứu của mình với định hướng về phân tích phi tuyến ứng xử uốn của kết cấu tấm FGM rỗng bằng phương pháp
giải tích với hai cách tiếp cận: theo chuyển vị và theo ứng suất (sử dụng hàm ứng suất Airy). Phân tích ổn định và
sau ổn định tấm FGM rỗng theo tiếp cận ứng suất. Với việc chọn hệ quy chiếu gắn với mặt trung hoà, các phương
trình cơ bản và hệ phương trình cân bằng chủ đạo xây dng theo hai mô hình tấm: lý thuyết biến dạng cắt bậc nhất
và lý thuyết tấm cổ điển nhận được sẽ đơn giản hơn so với cách tính trên mặt trung bình hình học.
CHƯƠNG 2. CƠ SỞ LÝ THUYẾT TÍNH TOÁN TẤM VẬT LIỆU FGM RỖNG CÓ KỂ ĐẾN YẾU TỐ
PHI TUYẾN HÌNH HỌC
2.1. Mở đầu
Phân tích phi tuyến ứng xử của các cấu kiện công trình là bài toán phức tạp nhưng rất có ý nghĩa thc tiễn
do phản ánh gần hơn s làm việc thc tế của kết cấu công trình. Với các loại vật liệu mới nói chung và vật liệu
FGM rỗng nói riêng thì hướng nghiên cứu này có tính thời s và tính cấp thiết. Trong chương này, tác giả sẽ trình
bày trường chuyển vị, biến dạng và nội lc theo lý thuyết biến dạng cắt bậc nhất và lý thuyết tấm cổ điển cho tấm
chữ nhật bằng vật liệu FGM rỗng có xét đến vị trí thc của mặt trung hòa. Các hệ thức cơ bản và phương trình chủ
đạo được thiết lập trên cơ sở xét đến độ võng lớn (kể đến thành phần biến dạng phi tuyến von Kárman) với hệ tọa
độ quy chiếu gắn với mặt trung hòa.
2.2. Mô hình tấm bằng vật liệu FGM rỗng
Để thiết lập các hệ thức và phương trình chủ đạo của tấm FGM rỗng, các tọa độ chiều dày trong hệ tọa độ quy
chiếu đi qua mặt trung bình và mặt trung hòa là ztb và zth được thể hiện trên hình (xem Hình 2.1).
Hình 2.1. Vị trí mặt trung bình và mặt trung hòa của tấm vật liệu FGM rỗng
Khoảng cách giữa mặt trung hòa và mặt trung bình được xác định theo [11,53]:
/2
/2
/2
/2
()
()
h
tb tb tb
h
h
tb tb
h
z E z dz
C
E z dz
(2.1)
Khi đó các đặc trưng cơ học của vật liệu FGM rỗng trong hệ tọa độ gắn với mặt trung hòa được thể hiện
theo công thức (2.2) - (2.4):
Dạng 1: Phân bố đều:
1 1 0
10
)
( ) ) ,
(1
, ( 1
th th
th
z
ze
E G z E G e

;
2
0
00
1 1 2 2
11e
ee




(2.2)
Dạng 2: Phân bố không đều - đối xứng:
(2.3)
3
Dạng 3: Phân bố không đều – bất đối xứng:
1 1 0 1
( ), ( ) , ; ( ) .
2 4 2 4
1 cos 1 cos
th th
th th th m
z C z C
E z G z E G z
hh
ee



(2.4)
trong đó:
;
22
th
hh
C z C
2.3. Lý thuyết biến dng cắt bậc nhất
2.3.1. Trường chuyển vị
Sử dụng hệ tọa độ quy chiếu đi qua mặt trung hòa, các thành phần chuyển vị
,,u v w
của điểm bất kỳ (x,
y, zth) trong không gian tấm được giả thiết [91]:
0 0 0
, , , , ; , , , , ; , , , .
th th x th th y th
u x y z u x y z x y v x y z v x y z x y w x y z w x y

(2.5)
2.3.2. Trường biến dạng
Theo lý thuyết biến dạng cắt bậc nhất, các thành phần biến dạng có kể đến thành phần phi tuyến hình học
von Kárman và xét đến độ không hoàn hảo hình học ban đầu
*
0,w
được thể hiện như dưới đây [51, 90, 91]:
2 * 2 *
, 0, 0, 0, 0, , , 0, 0, 0, 0, ,
,
**
, , 0, 0, 0, 0, 0, 0, 0, 0, , ,
, , 0, , , 0,
11
; ;
22
0;
;
; .
th
th th
x x x x x x th x x y y y y y y th y y
zz
xy y x y x x y y x x y th x y y x
xz x z x x yz y z y y
u u w w w z v v w w w z
w
u v u v w w w w w w z
w u w w v w

(2.6)
trong đó
**
00
,w w x y
là độ không hoàn hảo hình học ban đầu và được giả thiết nhỏ hơn chiều dày của tấm.
2.3.3. Trường ứng suất
Với giả thiết vật liệu FGM rỗng là đàn hồi tuyến tính, trường ứng suất trong tấm được xác định từ định
luật Hooke:
11 12
21 22
66
0
0;
00
xx
yy
xy xy
QQ
QQ
Q








55
44
0
0
th th
th th
xz xz
yz yz
Q
Q





(2.7)
2.3.4. Trường nội lực
Các thành phần nội lc trong tấm được xác định từ biểu thức định nghĩa:
0
11 12 0
12 11
0
66
0
0;
00
x
x
yy
xy xy
NAA
N A A
A
N









 
 
11 12
12 11
66
0
0 ;
00
xx
yy
xy xy
MCC
M C C
C
M





0
44
0
44
0
0
th th
th th
s
xz xz
s
yz yz
QA
QA





 



(2.8)
Từ (2.8) có thể thấy rằng, việc sử dụng hệ trục quy chiếu đi qua mặt trung hòa cho vật liệu FGM rỗng, tương
tác màng - uốn đã bị loại bỏ; từ đó quan hệ giữa ứng lc và biến dạng, cũng như hệ phương trình cân bằng theo chuyển
vị trở nên đơn giản hơn, các hệ thức này tương t như đối với vật liệu đẳng hướng.
2.3.5. Mối liên hệ giữa nội lực và chuyển vị
Từ (2.6) và (2.8) ta thu được biểu thức các thành phần nội lc theo các thành phần chuyển vị:
2 * 2 *
11 0, 0, 0, 0, 12 0, 0, 0, 0,
2 * 2 *
12 0, 0, 0, 0, 11 0, 0, 0, 0,
**
66 0, 0, 0, 0, 0, 0, 0, 0,
11
;
22
11
;
22
;
x x x x x y y y y
y x x x x y y y y
xy y x x y y x x y
N A u w w w A v w w w
N A u w w w A v w w w
N A u v w w w w w w
(2.9)