Giải phương trình
A.
B.
C.
D.
Câu 418
Cho phương trình:
. Tìm mọi
giá trị thực của m để phương trình có
nghiệm . Giá trị của m phải
tìm là :
A.
-1 ≤ m ≤ 0
B.
m > 0
C.
-2 < m < -
1
D.
1
≤ m ≤ 2
Câu 419
Giải phương trình:
A.
B.
C.
D.
Câu 420
Giải phương trình:
A.
B.
C.
D.
Câu 421
Cho . Tính trị số của
biểu thức
A.
B.
C. D.
Câu 422
Cho . Tính trị số của biểu
thức
A. B.
C.
D.
Câu 423
Cho . Tính
A.
B.
C.
D.
Câu 424
Cho . Tính
A.
B.
C.
D.
Câu 425
Cho . Tính
A.
B.
C.
D.
Câu 426
Cho . Tính
A.
B.
C. D.
Câu 427
Cho . Tính
A.
B.
C.
D.
Câu 428
Cho với . Tính
A. B.
C.
D.
Câu 429
Tìm nghiệm của phương trình
A.
B.
C. D.
Câu 430
Tìm nghiệm của phương trình
A. B.
C.
D.
Câu 431
Giải phương trình
A. B.
C.
D.
Câu 432
Giải phương trình
A.
B.
C.
D.
Câu 433
Giải phương trình
A.
B.
C.
D.
Câu 434
Giải phương trình
A.
B.
C.
D.
Câu 435
Giải phương trình
A.
B.
C.
D.
Câu 436
Giải phương trình
:
A.
B.
tu
ỳ ý thuộc R
C. D.
Câu 437
Giải phương trình
:
A. B.
C.
D.
A và B đ
ều đúng
Câu 438
Giải phương trình:
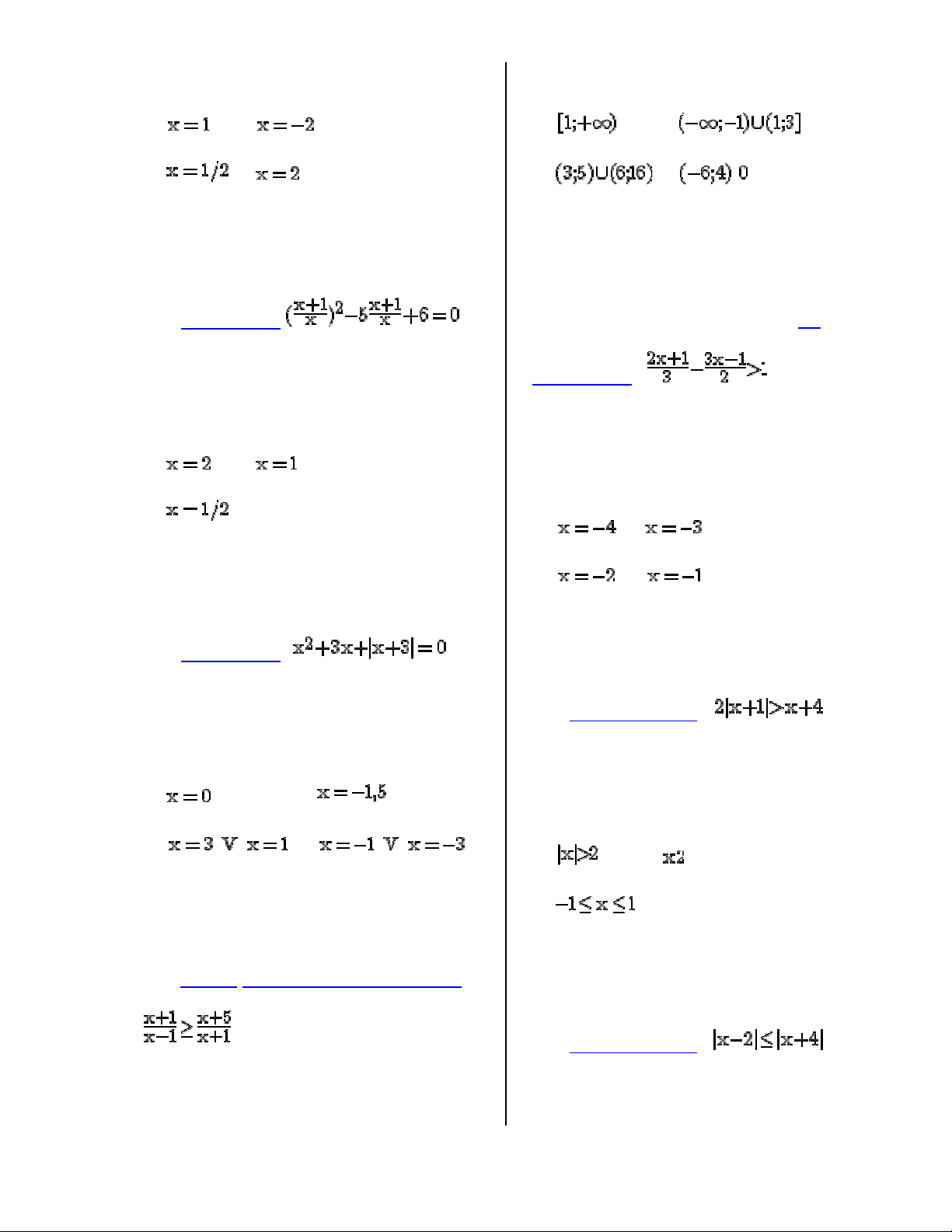
A. B.
C.
D.
Câu 439
Giải phương trình:
A. B.
C.
D. B và C đ
ều đúng
Câu 440
Giải phương trình:
A. B.
C.
D.
Câu 441
Tìm tập hợp nghiệm của bất phương trình :
A. B.
C.
D.
Câu 442
Tìm giá trị x nguyên lớn nhất thỏa bất
phương trình :
A.
B.
C.
D.
Câu 443
Giải bất phương trình :
A. B.
C.
D.
A và B đ
ều đúng
Câu 444
Giải bất phương trình :
