SỞ GIÁO DỤC VÀ ĐÀO TẠO
THÀNH PHỐ CẦN THƠ
Đề chính thức
KÌ THI CHỌN HỌC SINH GIỎI LỚP 9 THCS
CẤP THÀNH PHỐ-NĂM HỌC 2012-2013
Khóa ngày 11/04/2013
MÔN THI: TOÁN
Thời gian làm bài: 150 phút, không kể thời gian phát đề.
Câu 1 (5,0 điểm)
1. Cho biểu thức P=2m+√16m+ 6
m+ 2√m−3+√m−2
√m−1+3
√m+ 3 −2
a) Rút gọn P.
b) Tìm giá trị tự nhiên của mđể Plà số tự nhiên.
2. Tính giá trị (a3+ 15a−25)2013 với a=3
p13 −7√6 + 3
p13 + 7√6.
Câu 2 (5,0 điểm)
1. Giải phương trình: √x+ 5 + √3−x−2√15 −2x−x2+ 1= 0.
2. Tìm giá trị của mđể hệ phương trình sau có nghiệm:
2x2+mx −1 = 0
mx2−x+ 2 = 0
Câu 3 (5,0 điểm)
1. Tìm tất cả các số nguyên dương x, y, z thỏa 1
x+1
y+1
z= 2.
2. Cho hai số x, y thỏa mãn: x+y≤2
x2+y2+xy = 3
Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức T=x2+y2−xy.
Câu 4 (2,0 điểm)
Cho đường tròn (O;R)và hai điểm A, B nằm ngoài đường tròn sao cho OA = 2R. Tìm điểm M
trên đường tròn để MA + 2MB đạt giá trị nhỏ nhất.
Câu 5 (3,0 điểm)
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O;R). Gọi Plà một điểm di động trên
cung BC không chứa A.
1. Gọi M, N lần lượt là hình chiếu vuông góc hạ từ Axuống P B, P C. Chứng minh rằng đường
thẳng MN luôn đi qua một điểm cố định.
2. Gọi I, D, E là chân các đường cao lần lượt hạ từ A, B, C xuống các cạnh BC, CA, AB.
Chứng minh rằng chu vi tam giác IDE không đổi khi A, B, C thay đổi trên đường tròn
(O;R)sao cho diện tích của tam giác ABC luôn bằng a2.
—–HẾT—–
Ghi chú: Giám thị coi thi không giải thích gì thêm.
SỞ GIÁO DỤC VÀ ĐÀO TẠO
THÀNH PHỐ CẦN THƠ
Đề chính thức
KÌ THI CHỌN HỌC SINH GIỎI LỚP 9 THCS
CẤP THÀNH PHỐ-NĂM HỌC 2012-2013
Khóa ngày 11/04/2013
MÔN THI: TOÁN
Thời gian làm bài: 150 phút, không kể thời gian phát đề.
HƯỚNG DẪN CHẤM
(Hướng dẫn chấm này có 03 trang.)
CÂU NỘI DUNG ĐIỂM
1(5,0đ)
1. (3,5 điểm)
a) Điều kiện: m≥0, m 6= 1 0,5đ
P=√m+ 1
√m−12,0đ
b) P= 1 + 2
√m−10,5đ
Để P∈N=⇒m∈ {4; 9}0,5đ
2.(1,5 điểm)
a=3
p13 −7√6 + 3
p13 + 7√6 =⇒a3= 26 −15a1,0đ
a3+ 15a−25 = 1 =⇒(a3+ 15a−25)2013 = 1 0,5đ
2(5,0đ)
1. (2,5 điểm)
Điều kiện: −5≤x≤30,5đ
Đặt t=√x+ 5 + √3−x, t2= 8 + 2√15 −2x−x2=⇒t≥2√2
Phương trình đã cho có dạng: t2−t−6 = 0 ⇐⇒ t= 3
t=−2(loại) 1,0đ
t= 3 ⇐⇒ √x+ 5 + √3−x= 3
⇐⇒ 4x2+ 8x−59 = 0 ⇐⇒
x=−2 + 3√7
2
x=−2−3√7
2
1,0đ
2. (2,5 điểm)
Đặt x2=y≥0. Hệ trở thành: mx + 2y= 1
−x+my =−20,5đ
Hệ luôn có nghiệm:
x=m+ 4
m2+ 2
y=1−2m
m2+ 2 ≥0 (m≤1
2)
0,5đ
Ta có: x2=y⇐⇒ m+ 4
m2+ 22
=1−2m
m2+ 2 0,5đ
⇐⇒ (m+ 1) (m2−m+ 7) = 0 ⇐⇒ m=−11,0đ
3(5,0đ) 1. (3,0 điểm)
Tiếp
CÂU NỘI DUNG ĐIỂM
Không mất tính tổng quát giả sử: 1≤x≤y≤z
=⇒2 = 1
x+1
y+1
z≤3
x=⇒x= 1
1,0đ
=⇒1
y+1
z= 1 ≤2
y=⇒y= 1 (vô lý)
y= 2 =⇒z= 2 1,0đ
Vậy (1; 2; 2) và các hoán vị của chúng là nghiệm của phương trình đã cho 1,0đ
2. (2,0 điểm)
Hệ (x+y≤2
x2+y2+xy = 3 ⇐⇒ (x+y= 2 −a(a≥0)
x2+y2+xy = 3 0,5đ
Do đó: (x+y= 2 −a
xy = (2 −a)2−3,∆ = S2−4P≥0 =⇒0≤a≤40,5đ
T=x2+y2+xy −2xy = 9 −2(2 −a)20,5đ
min T= 1 khi x= 1, y = 1 hoặc x=−1, y =−1
max T= 9 khi x=√3, y =−√3hoặc x=−√3, y =√3
0,5đ
4(2,0đ)
O
A
B
C
M
M′
Gọi Clà điểm trên đoạn thẳng OA sao cho OC =R
2, ta có điểm Ccố định 0,5đ
Dễ thấy ∆OCM đồng dạng ∆OMA =⇒MA = 2MC 0,5đ
Ta có MA +MB ≥BC (không đổi)
MA + 2MB = 2(MB +MC)≥2BC
0,5đ
Dấu “=” xảy ra khi và chỉ khi Mnằm giữa Bvà C
Vậy khi điểm Mlà giao điểm của đoạn BC và đường tròn (O)thì MA+2MB
đạt giá trị nhỏ nhất 0,5đ
5(3,0đ) 1. (2,0 điểm)
Tiếp
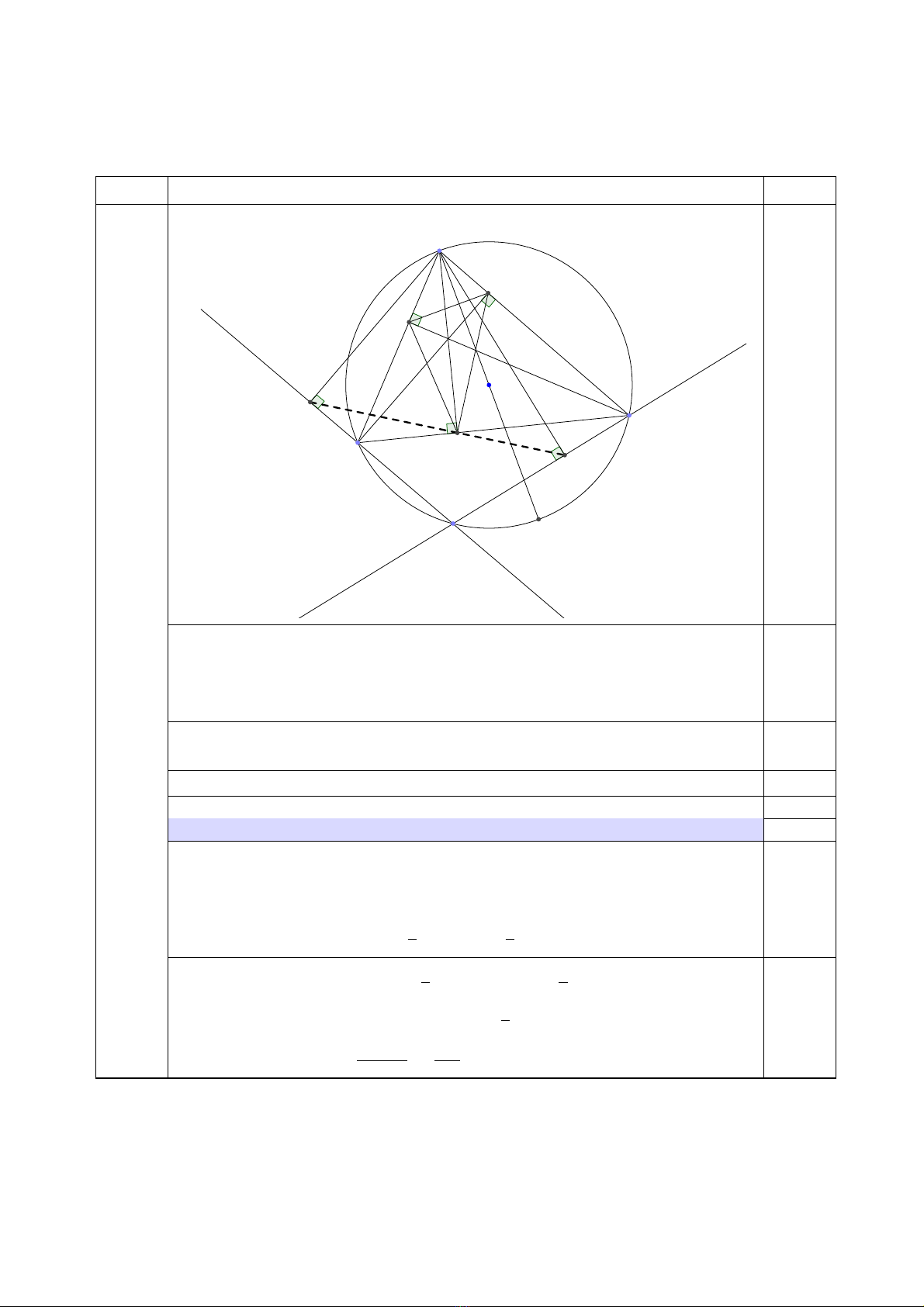
CÂU NỘI DUNG ĐIỂM
O
A
B
C
P
N
D
I
E
M
A′
Kẻ AI ⊥BC, I ∈BC cố định. Ta có \
BM A =[
BIA = 90◦nên tứ giác
AMBI nội tiếp hay [
AIM =\
ABM
Ta lại có tứ giác ABP C nội tiếp nên \
ABM =[
ACP
Do đó [
AIM =[
ACP (1)
1,0đ
Mặt khác [
AIC =\
ANC = 90◦nên tứ giác AINC nội tiếp, suy ra
[
ACP +[
AIN = 180◦(2)
0,5đ
Từ (1) và (2) suy ra [
AIM +[
AIN = 180◦0,5đ
Vậy đường thẳng MN luôn đi qua điểm cố định I
2. (1,0 điểm)
Tứ giác BCDE nội tiếp suy ra \
AED =[
ACB
Kéo dài AO cắt (O;R)tại điểm A′. Ta có:
[
EAO +\
AED =\
BAA′+[
ACB = 90◦
=⇒AO ⊥DE =⇒SAEOD =1
2AO.DE =1
2R.DE
0,5đ
Tương tự ta cũng có: SBEOI =1
2R.EI, SCDOI =1
2R.ID
Vậy: SABC =SAEOD +SBIOE +SCDOI =1
2R.(DE +EI +ID)
=⇒DE +EI +ID =2SABC
R=2a2
R(không đổi)
0,5đ
—–HẾT—–
Ghi chú:
•Mọi cách giải đúng khác đáp án đều cho điểm tối đa.