Tuyển tập Hội nghị Khoa học thường niên năm 2024. ISBN: 978-604-82-8175-5
294
XÁC ĐỊNH THAM SỐ FRACTAL TỪ ĐỘ THẤM TỶ ĐỐI
CỦA MÔI TRƯỜNG LỖ RỖNG
Nguyễn Mạnh Hùng, Lương Duy Thành
Trường Đại học Thủy lợi, email: nguyenmanhhung@tlu.edu.vn
1. GIỚI THIỆU CHUNG
Độ thấm của môi trường lỗ rỗng là một
tham số quan trọng, đặc trưng cho khả năng
truyền dẫn nước. Độ thấm có vai trò quan
trọng trong thuỷ văn, nông nghiệp, địa kỹ
thuật, khai thác dầu khí, v.v. Kết quả thực
nghiệm chỉ ra độ thấm phụ thuộc vào đặc
điểm của môi trường lỗ rỗng như kích thước
lỗ rỗng, sự phân bố lỗ rỗng, sự kết nối giữa
chúng, độ rỗng, độ bão hoà v.v. [1, 2]. Có
nhiều phương pháp được sử dụng để nghiên
cứu các hiện tượng truyền dẫn nói chung và
hiện tượng thấm nói riêng trong môi trường
lỗ rỗng như phương pháp trung bình thể tích,
phương pháp môi trường hiệu dụng, v.v.. Tuy
nhiên, một trong các phương pháp đơn giản
và được sử dụng phổ biến là phương pháp
mô hình ống mao dẫn (OMD) [1-4]. Có nhiều
công bố liên quan đến độ thấm của môi
trường lỗ rỗng sử dụng mô hình OMD dưới
điều kiện bão hoà [2] và chưa bão hoà [1, 4].
Các công bố đó đều tập trung vào việc tính
độ thấm từ đặc điểm của môi trường lỗ rỗng.
Tuy nhiên, như tìm hiểu của chúng tôi, chưa
có một công bố nào đề xuất tính tham số
fractal D từ mối quan hệ giữa độ thấm tỷ đối
và độ bão hoà của môi trường. Cần chú ý
rằng, tham số D thường được xác định bằng
thực nghiệm qua phương pháp đếm hộp [1].
Do vậy, trong báo cáo này, chúng tôi xây
dựng mô hình cho độ thấm và độ thấm tỷ đối
của môi trường lỗ rỗng dưới điều kiện chưa
bão hòa sử dụng mô hình OMD. Mô hình thu
được được so sánh và kiểm chứng với các số
liệu thực nghiệm đã công bố. Ngoài ra, từ mô
hình thu được, chúng tôi đề xuất tính tham số
fractal D từ kết quả thực nghiệm cho độ thấm
tỷ đối.
2. PHƯƠNG PHÁP NGHIÊN CỨU
Trong trường hợp tổng quát, môi trường lỗ
rỗng được cấu thành bởi ba pha vật chất: pha
rắn (các hạt khoáng chất), pha lỏng (nước) và
pha khí (không khí). Tùy theo hàm lượng
nước có trong lỗ rỗng, mà độ bão hòa (độ bão
hòa Sw là tỷ số giữa thể tích của nước chứa
bên trong các lỗ rỗng và thể tích tổng cộng
của các lỗ rỗng trong môi trường) khác nhau
và các hiện tượng xảy ra trong đó cũng có thể
khác nhau. Môi trường lỗ rỗng khô được cấu
thành bởi hai pha rắn và pha khí, nên độ bão
hòa Sw = 0. Ngược lại, môi trường có các lỗ
rỗng chứa lấp đầy nước được cấu thành bởi
hai pha rắn và lỏng, độ bão hòa Sw = 1. Môi
trường lỗ rỗng chưa bão hòa (một phần lỗ
rỗng vẫn còn chứa khí) được cấu thành bởi
ba pha rắn, lỏng và khí nên độ bão hòa có giá
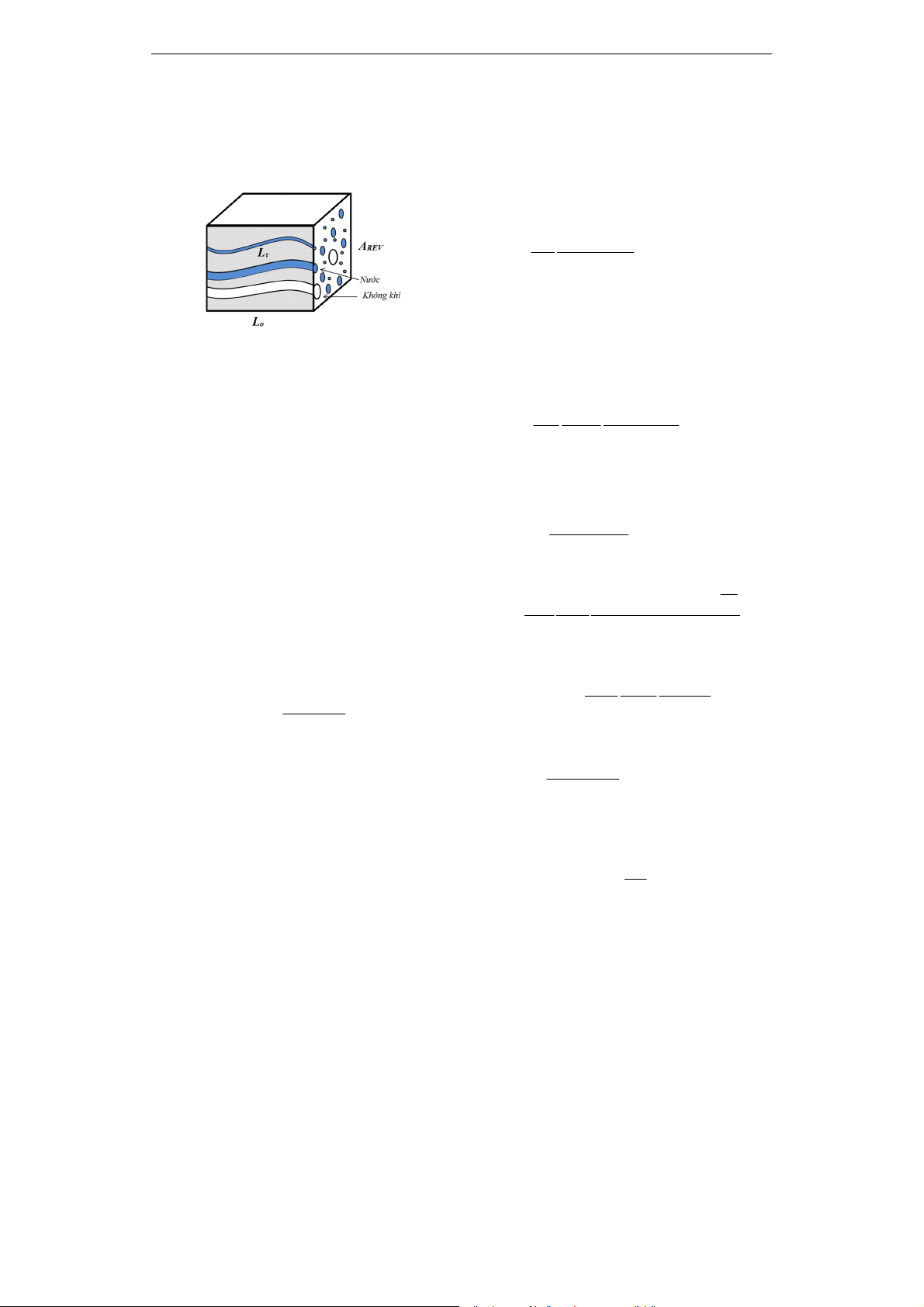
trị trong khoảng 0 < Sw < 1). Hình 1 minh
họa môi trường lỗ rỗng bão hoàn toàn và
chưa bão hòa.
Hình 1. Minh họa môi trường
lỗ rỗng bão hòa hoàn toàn (bên trái)
và chưa bão hòa (bên phải)
Sử dụng phương pháp tương tự như trình
bày trong công bố [2], chúng tôi xét một khối
lỗ rỗng cơ sở hình lập phương (REV) có chiều
dài L0 (m) và tiết diện ngang AREV (m2) vuông
góc với hướng dòng chảy (hình 2). Theo mô
hình OMD, khối REV được coi gần đúng như
tập hợp của các ống mao dẫn hình trụ song