
Bài 4 : VỊ TRÍ TƯƠNG ĐỐI CỦA ĐƯỜNG THẲNG VÀ ĐƯỜNG TRÒN
I/ MỤC TIÊU :
- HS nắm được ba vị trí tương đối của đthẳng và đường tròn , các KN
tiếp tuyến , tiếp điểm . Nắm được định lí về tính chất của tiếp tuyến . nắm
được các hệ thức giữa khoảng cách từ tâm đường tròn đến đường thẳng và
bán kính đtròn ứng với từng vị trítương đối của đường thẳng và đường
tròn .
- Biết vận dụng các k.thức trong bài để nhận biết các vị trí tương đối của
đ.thẳng và đường tròn
- Thấy được một số hình ảnh về vị trí tương đối của đthẳng và đtròn trong
thực tế .
II/ CHUẨN BỊ :
+ Thước thẳng , compa , êke .
III/ TIẾN TRÌNH LÊN LỚP :
1/ On định :
2/ KTBC :
- GV : (?) Hãy nêu vị trí tương đối của một điểm đối với đường tròn .
- HS : (TL) Cho đtròn và 1 điểm M
o Nếu OM’ = R -> M’ nằm trên đtròn (O) .
o Nếu OM” > R -> M” nằm ngoài đtròn (O) .
o Nếu OM < R -> M nằm trong đtròn (O) .
M’ M”
- GV : Cho HS vẽ hình biểu diễn điểm M ở 3 vị trí đã nêu trên .
3/ Bài mới : < GV giới thiệu tên bài > .
Hoạt động của GV Hoạt động cuả
HS Nội dung
- (?) Tại sao 1 đthẳng và
1 đtròn không thể có
nhiều hơn 2 điểm chung
?
- Chốt lại : Nếu 1 đthẳng
và 1 đtròn có 3 điểm
chung trở lên thì đường
tròn đi qua 3 điểm thẳng
hàng ( Vô lý ).
- Giới thiệu mục a .
- HS :
TL……………
……………..
-HS lắng nghe
GV hướng dẫn
và ghi vào vở .
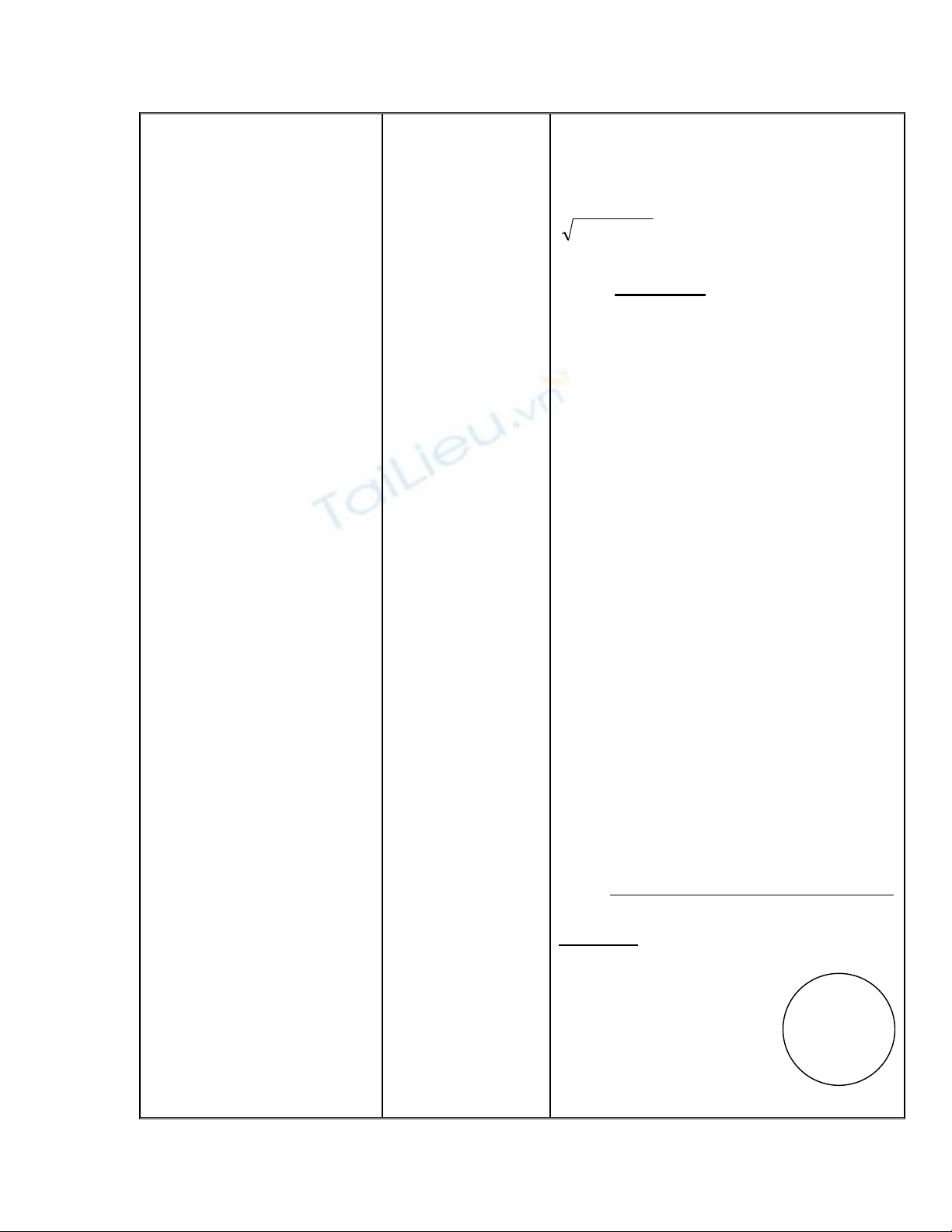
1/ Ba vị trí tương đối của đường
thẳng và đường tròn :
a/ Đường thẳng và đường tròn cắt
nhau :
Đường thẳng a và (O) có
2 điểm A , B .Ta nói
đường thẳng a và (O)
cắt nhau , đthẳng a còn
O M
- GV giới thiệu vị trí
đường thẳng và đường
tròn cắt nhau trong 2 TH
sau
- GV hướng dẫn HS
chứng minh .
- GV chốt lại ghi bảng
chứng của HS .
- GV sử dụng thước
thẳng di chuyển đthẳng
d1 đến vị trí d2 và hỏi nếu
k/c OH tăng lên thì k/c
giữa 2 điểm A và B giảm
đi . Khi 2 điểm A và B
trùng nhau thì đthẳng a
và đtròn (O) ntn với nhau
?
- GV chốt lại chuyển
- HS nêu cách
chứng minh .
- HS nhận xét ?
- HS TL
………………
…..
gọi là cát tuyến của (O) .
Khi đó OH < R và AH = HB =
22 OHR
Vận dụng : Làm ? 2 <
SGK/108 >
Chứng minh
+ T.hợp 1 : Đthẳng a đi qua tâm của
đtròn .
=> Khoảng cách từ O -> a bằng 0
Nên OH = 0 < R
+ T.hợp 2 : Đthẳng a không đi qua
tâm của đtròn .
Kẻ OH
AB = { H}
Xét
OHB vuông tại H , ta có :
OH < OB => OH < R
b/ Đường thẳng và đường tròn tiếp
xúc nhau
Khi đường thẳng a và (O)
có 1 điểm C chung duy
nhất . Ta nói đthẳng a
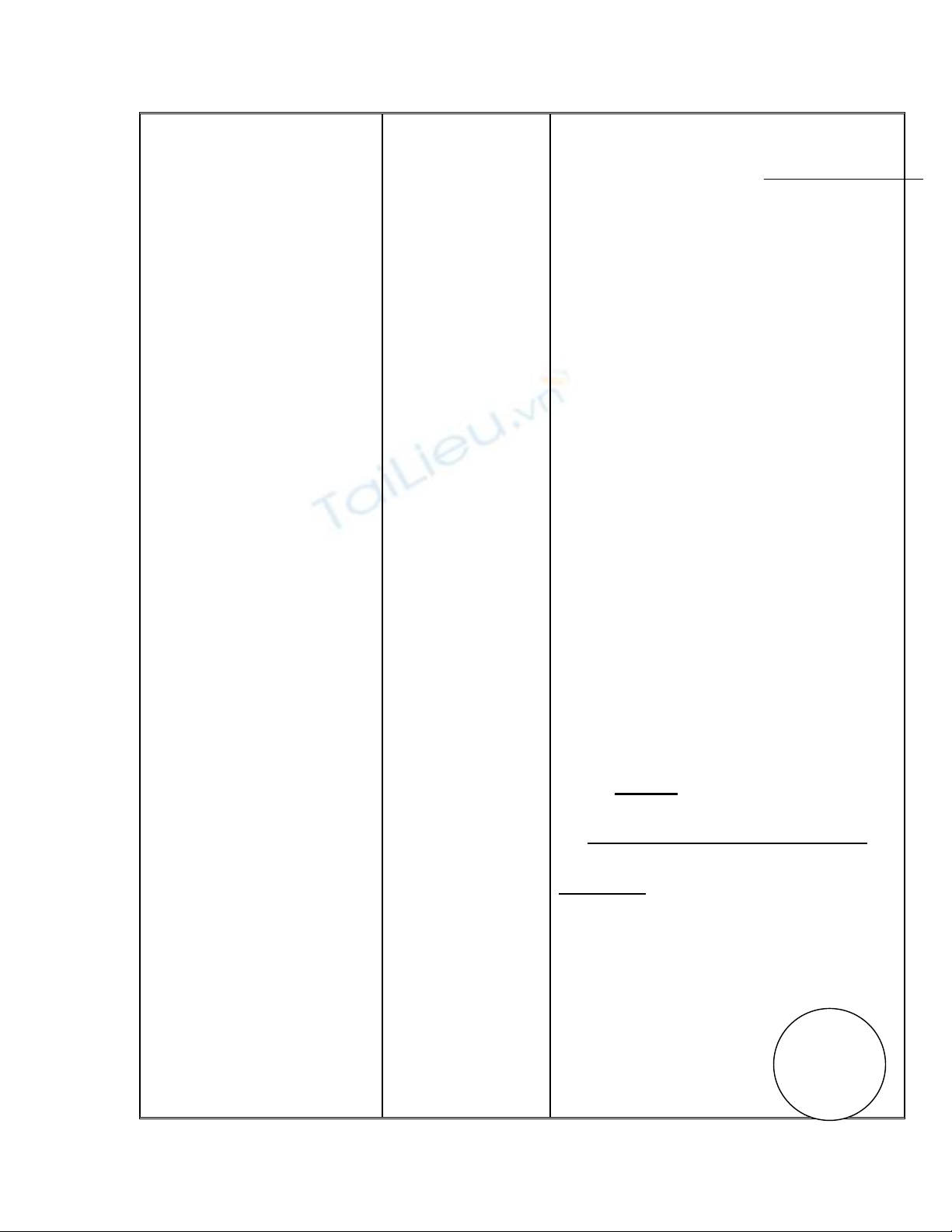
sang mục b .
- GV giới thiệu vị trí
Đường thẳng và đường
tròn tiếp xúc nhau trong 2
TH sau
- GV hướng dẫn HS CM
.
- Chốt lại và nêu định lí
- GV vẽ hình lên bảng và
giới thiệu đthẳng và đtròn
không giao nhau .
- Gọi 1 HS so sánh
khoảng cách từ tâm của
đt-> đthẳng a và bán kính
của đtròn ntn ?
- Chốt lại nhận xét và ghi
bảng .
- GV chuyển ý sang mục
2
-(?) Qua 3 vị trí t.đối của
-HS lắng nghe
GV hướng dẫn
và ghi vào vở .
- HS lắng nghe
GV nêu cách
chứng minh và
ghi vào vở .
- HS nhắc lại và
ghi vào vở .
- HS :
TL……………
…..
- HS ghi vào vở .
- TL
………………
……..
và đt(O) tiếp xúc nhau .
Ta còn nói đthẳng a là
tiếp tuyến củ
a H
D
đt(O) . Điểm C gọi là tiếp điểm .
Khí đó :OH = R
Chứng minh
Vì OH = R
( ; )
H O R
Ta lấy D
a (D≠ H)
Xét ∆ODH có ˆ
1
H v
OD OH
( T/chất tam giác
vuông )
OD R
D nằm ngoài (O;R)
Định lí : < SGK/ 108 >
c/ Đ thẳng và đường tròn không
giao nhau
Khi đường thẳng a và đt(O)không có
điểm chung ta nói
đthẳng và đt(O)
không giao
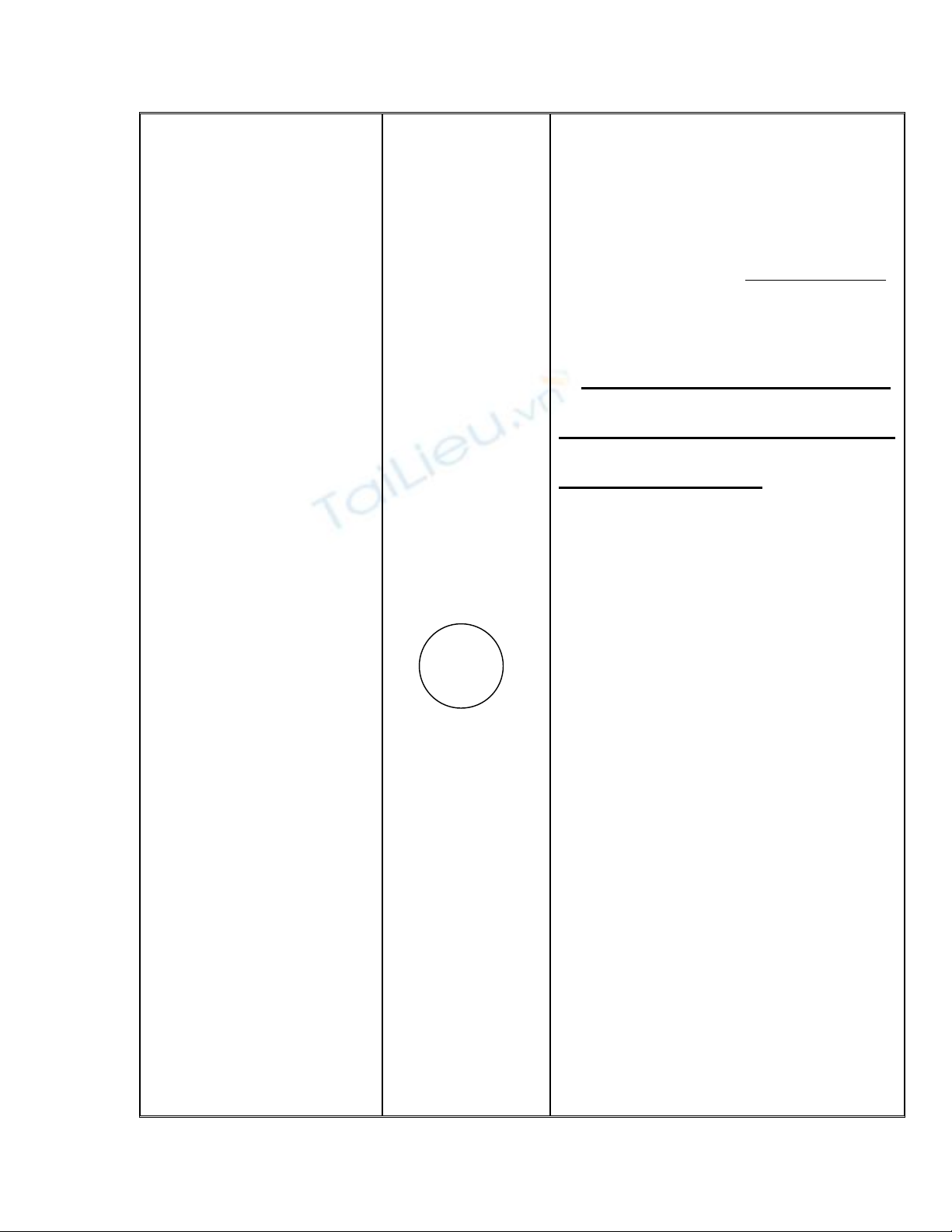
đthẳng đối với đtròn ta có
thể rút ra được K.luận gì
?
- GV chốt lại ghi bảng và
hỏi
+ Nếu a
(O) thì d ntn
R ?
+ Nếu a t.xúc với (O) thì
d ntn R ?
+ Nếu đt a không giao
với (O) thì d ntn R ?
- Ngược lại ,
+ Nếu d < R => ?
+ Nếu d = R => ?
+ Nếu d > R => ?
- GV chốt lại cho HS ghi
bảng tóm tắt SGK / 109
- GV cho HS làm ?3 <
SGK/ 109 >
- Chốt lại và củng cố ,
- TL
………………
……..
- TL
………………
……..
- TL
………………
……..
- HS làm ? 3
a/ đthẳng a
(O) vì d < R
b/ Kẻ OH
a
hay OH
BC ta
tính được HC =
4 => BC = 8 cm
nhau . Khi đó OH > R
2/ Hệ thức giữa khoảng cách từ tâm
đường tròn đến đường thẳng và bán
kính của đương tròn :
< SGK / 109 >
















