CHUỖI SỐ VÀ CHUỖI LŨY THỪA
Chương 5:
Phần 1: CHUỖI SỐ
ĐỊNH NGHĨA
1 2
,
n n
S a a a n N= + + + L
Cho dãy số {an}, định nghĩa dãy số mới
{Sn} được gọi là chuỗi số, ký hiệu:
1
n
n
a
=
( Nếu {an} bắt đầu từ a0 thì số hạng đầu
của Sn là a0 )
• Sn : tổng riêng thứ n
• an : số hạng tổng quát
ĐỊNH NGHĨA
1
n
n
a
=
{Sn} có giới hạn hữu hạn khi n
hội tụ
Ngược lại ta nói chuỗi phân kỳ.
Đặt:
1
lim
n n
n
n
a S
==
: tổng chuỗi
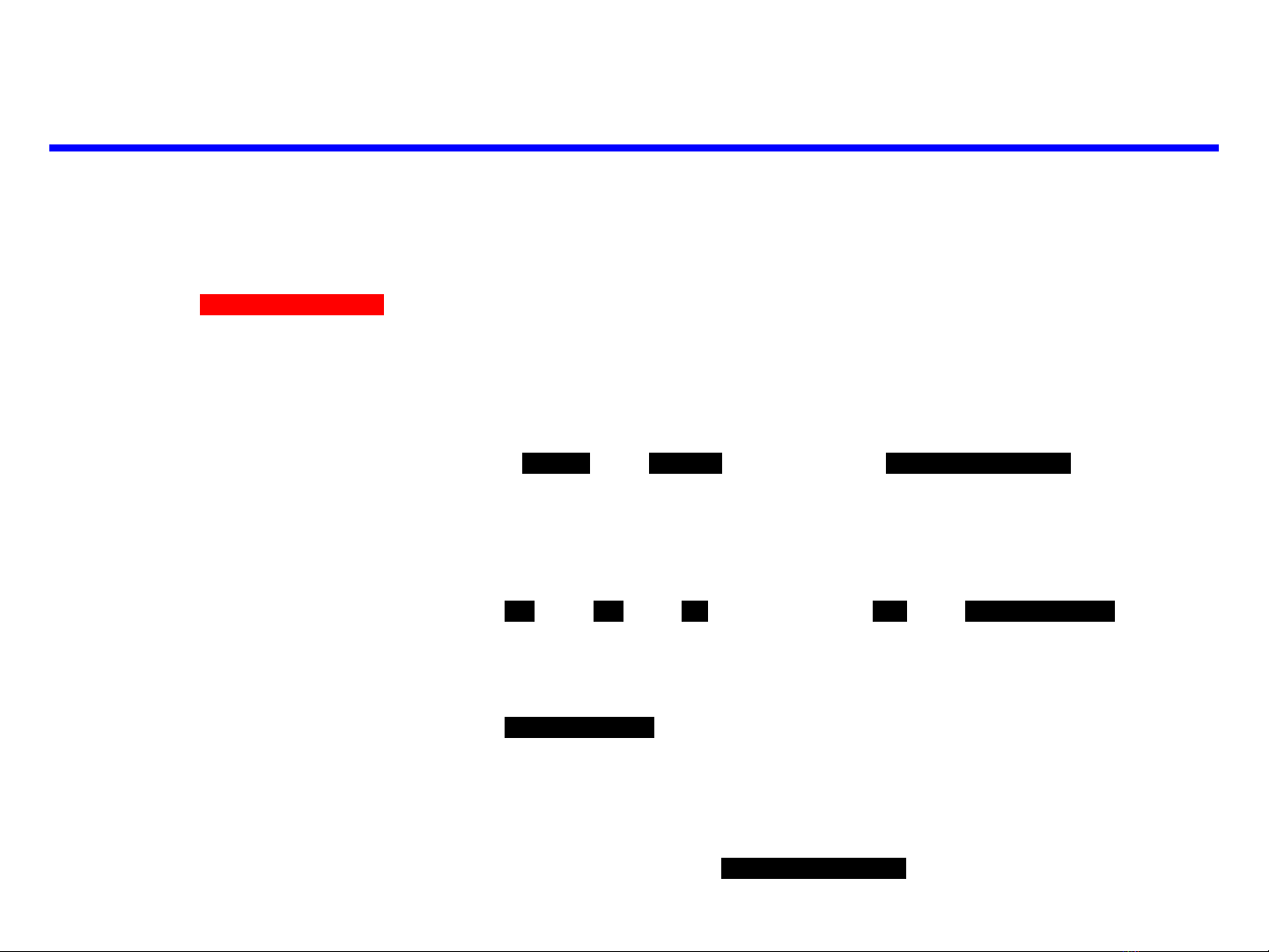
VÍ DỤ
1
1
( 1
1/ )
nn n
=+
1 1 1
1.2 2.3 ( 1)
n
Sn n
= + + + +
L
1 1 1 1 1
12 2 3 ( 1)n n
= − + − + + − +
L
Khảo sát sự hội tụ và tính tổng nếu có:
Tổng riêng:
1
1( 1)n
= − +1
n
1
11
( 1)
nn n
==
+
Vậy chuỗi hội tụ và
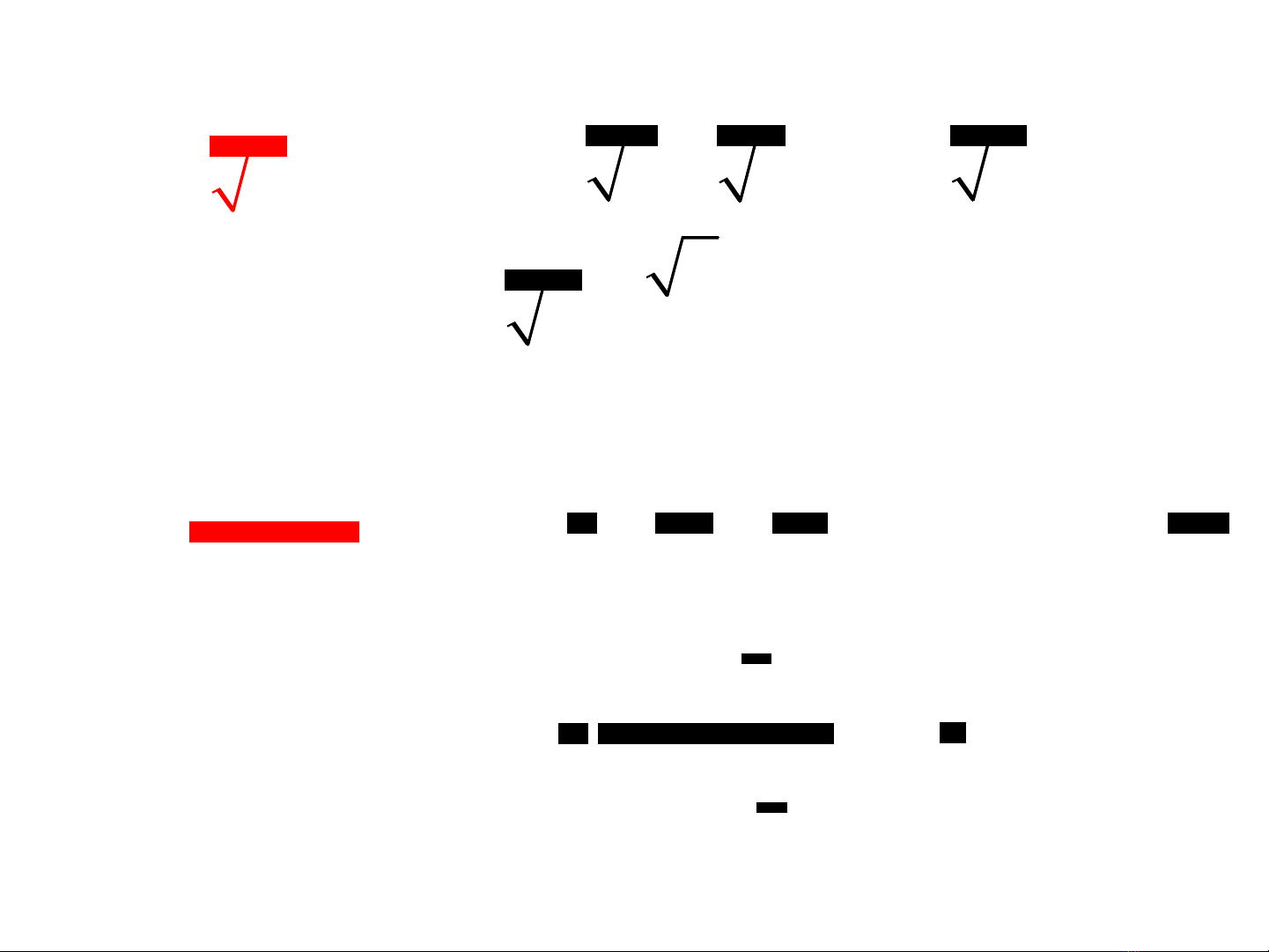
1
2 / 1
nn
=
1 1 1
12 3
n
Sn
= + + + +L
nn
n
=
Vậy chuỗi phân kỳ.
1
1
3( 1)
2
/
n
n
n
+
=
−
1
2 3
1 1 1 1
( 1)
22 2 2
n
nn
S+
= − + − + −L
1
1
12
1
212
n
� �
− −
� �
� �
=� �
− −
� �
� �
1
3
Vậy chuỗi hội tụ và có tổng là 1/3.