GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bôSlide 1106
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bôSlide 1107
§1. Các khái niệm cơ bản
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bô Slide 1109
b. Phân loại hình dạng: dựa vào kích thước ba chiều của vật thể.
Tấm
Vỏ
Tấm – vỏ Thanh
Trong giới hạn chương trình, ta chỉ nghiên cứu thanh mà thôi
Khối
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bôSlide 1108
1. Vật rắn biến dạng
a. Vật rắn biến dạng: là vật rắn mà dưới tác dụng của ngoại lực vật sẽ
thay đổi về hình dạng và kích thước so với trạng thái ban đầu của vật.
+ Hình dạng và kích thước ban đầu
+ Hình dạng và kích thước khi chịu ngoại lực
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bô Slide 1110
c. Các hiện tượng biến dạng
Biến dạng
-Biến dạng dài
-Biến dạng góc
-Biến dạng thể tích
Hình thức
-Biến dạng đàn hồi
-Biến dạng dẻo (dư)
-Biến dạng nhớt
Tính chất
• Biến dạng dài: Sự thay đổi chiều dài
• Biến dạng góc: Sự thay đổi góc vuông
• Biến dạng thể tích: Sự thay đổi thể tích
• Biến dạng đàn hồi: mất đi khi loại bỏ nguyên nhân gây biến dạng
• Biến dạng dẻo (dư): không mất đi khi loại bỏ nguyên nhân gây biến dạng
• Biến dạng nhớt: không xảy ra tức thời mà biến đổi theo thời gian
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bô Slide 1111
d. Những giả thiết về vật liệu của đối tượng nghiên cứu
+ Giả thuyết 2: Vật liệu đàn hồi tuyệt đối và tuân theo định luật Hooke.
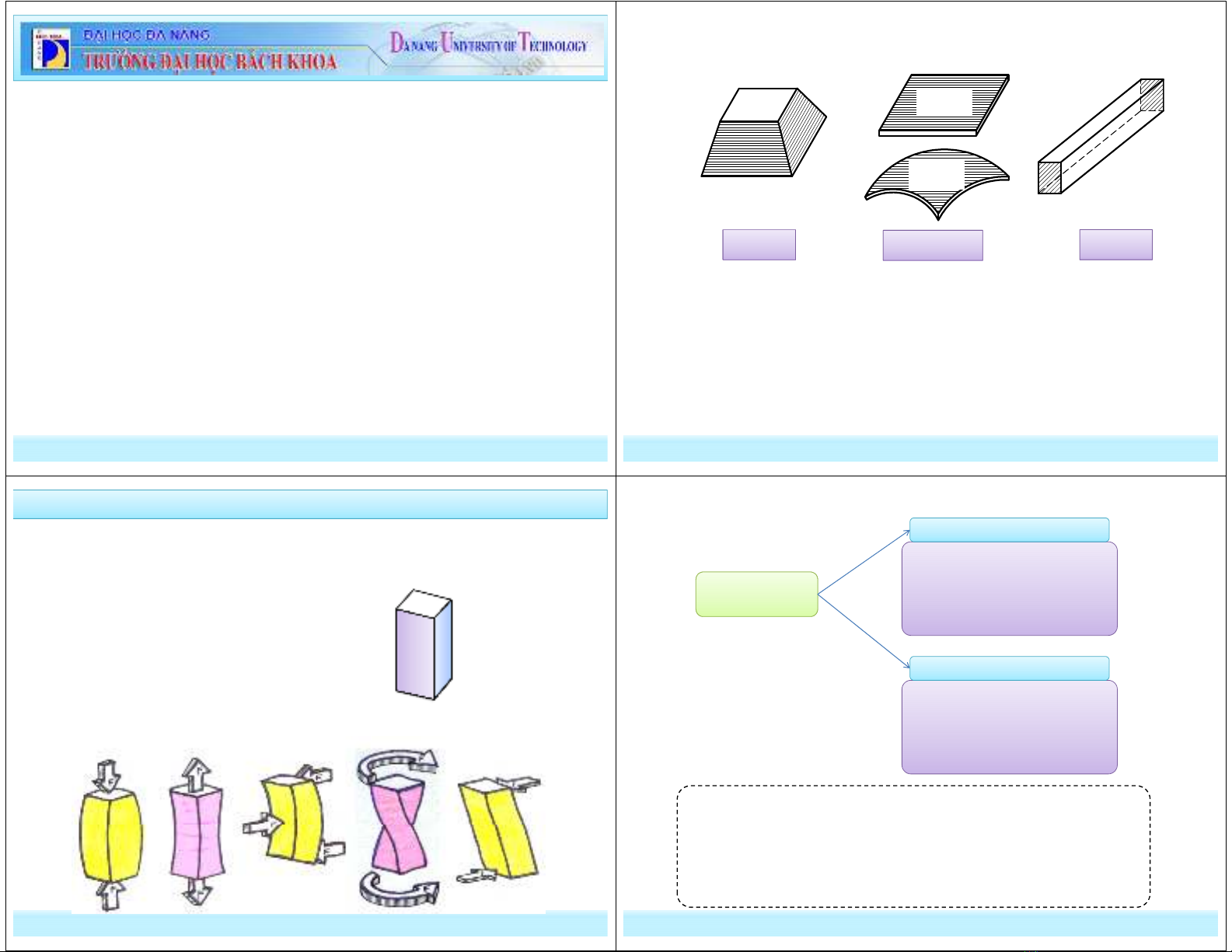
- Vật liệu đàn hồi tuyệt đối: Khi ngoại lực tác dụng, vật thể bị thay đổi
hình dạng, kích thước ban đầu; thôi tác dụng, vật thể có khả năng quay về
đúng hình dạng và kích thước ban đầu.
- Vật liệu làm việc tuân theo định luật Hooke: Quan hệ giữa lực và biến
dạng là bậc nhất, phương trình quan hệ có dạng f(x) = kx.
- Vật liệu đàn hồi tuyến tính khi thỏa mãn giả thuyết 2
- Vật liệu liên tục: Vật liệu chiếm đầy không gian vật thể.
- Vật liệu đồng chất: Tính chất cơ lý tại mọi điểm của vật thể giống nhau.
- Vật liệu đẳng hướng: Tính chất cơ lý xung quanh một điểm bất kỳ và
theo hướng bất kỳ như nhau.
+ Giả thuyết 1: Vật liệu có tính liên tục, đồng chất và đẳng hướng.
+ Giả thuyết 3: Biến dạng của vật thể là bé.
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bôSlide 1113
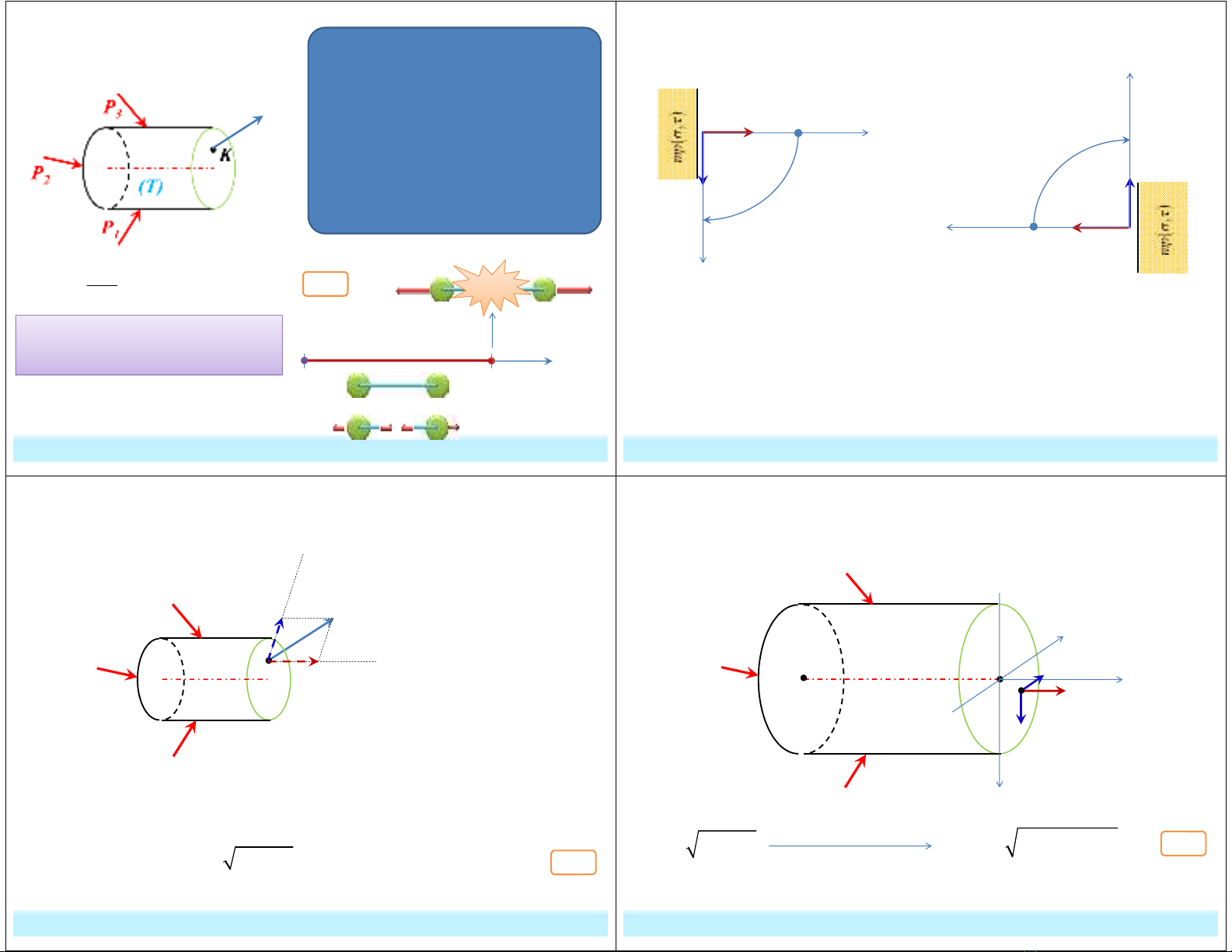
2. Đặc trưng hình học của thanh và biểu diễn thanh trong sơ đồ tính
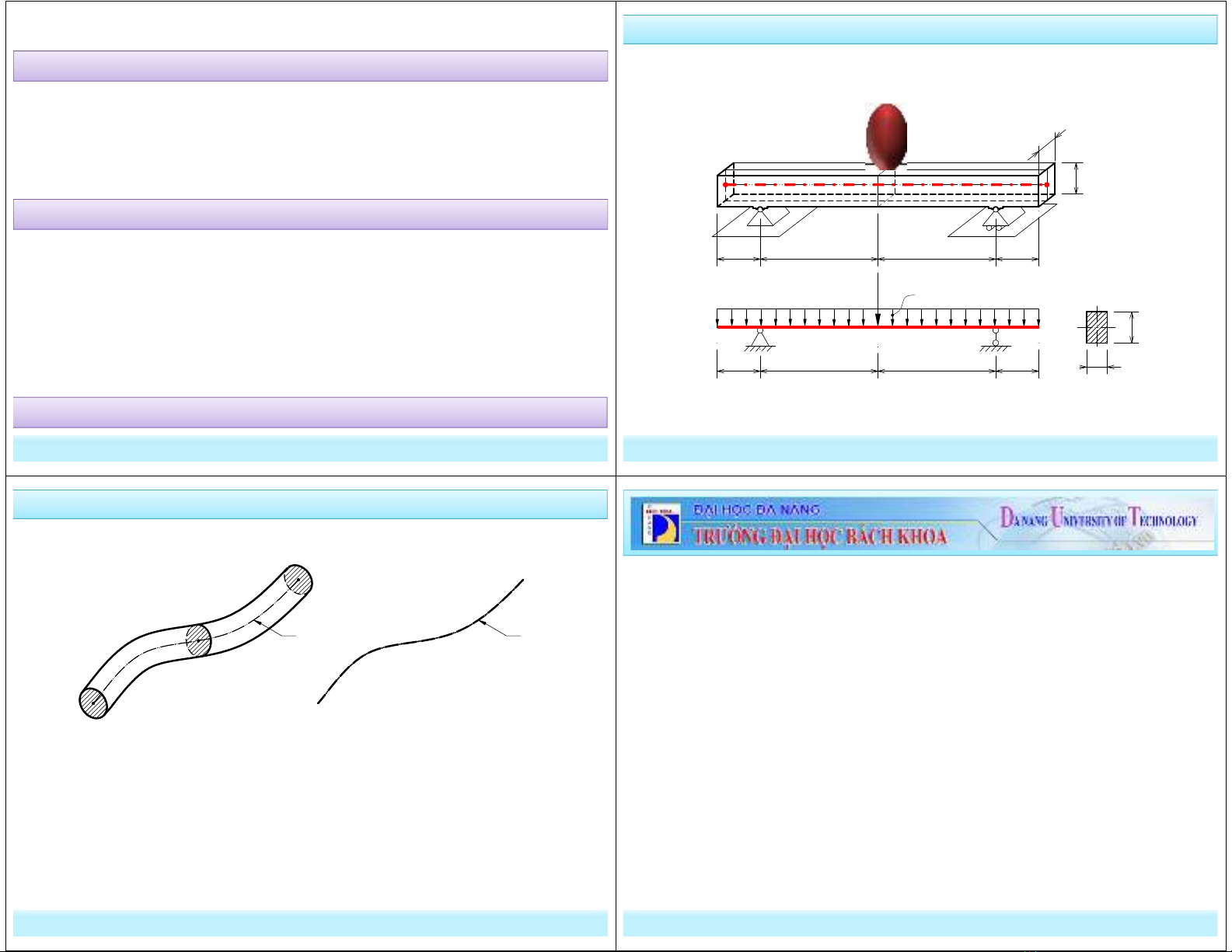
b. Biểu diễn thanh trong sơ đồ tính: bằng trục thanh (nét liền đậm) và
kích thước hình học của hệ.
Sơ đồ tính Mcn
P
h
b
b
h
P
l
a a
a a
q
l
l l
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bô Slide 1112
2. Đặc trưng hình học của thanh và biểu diễn thanh trong sơ đồ tính
F
F
(C)
F
(C)
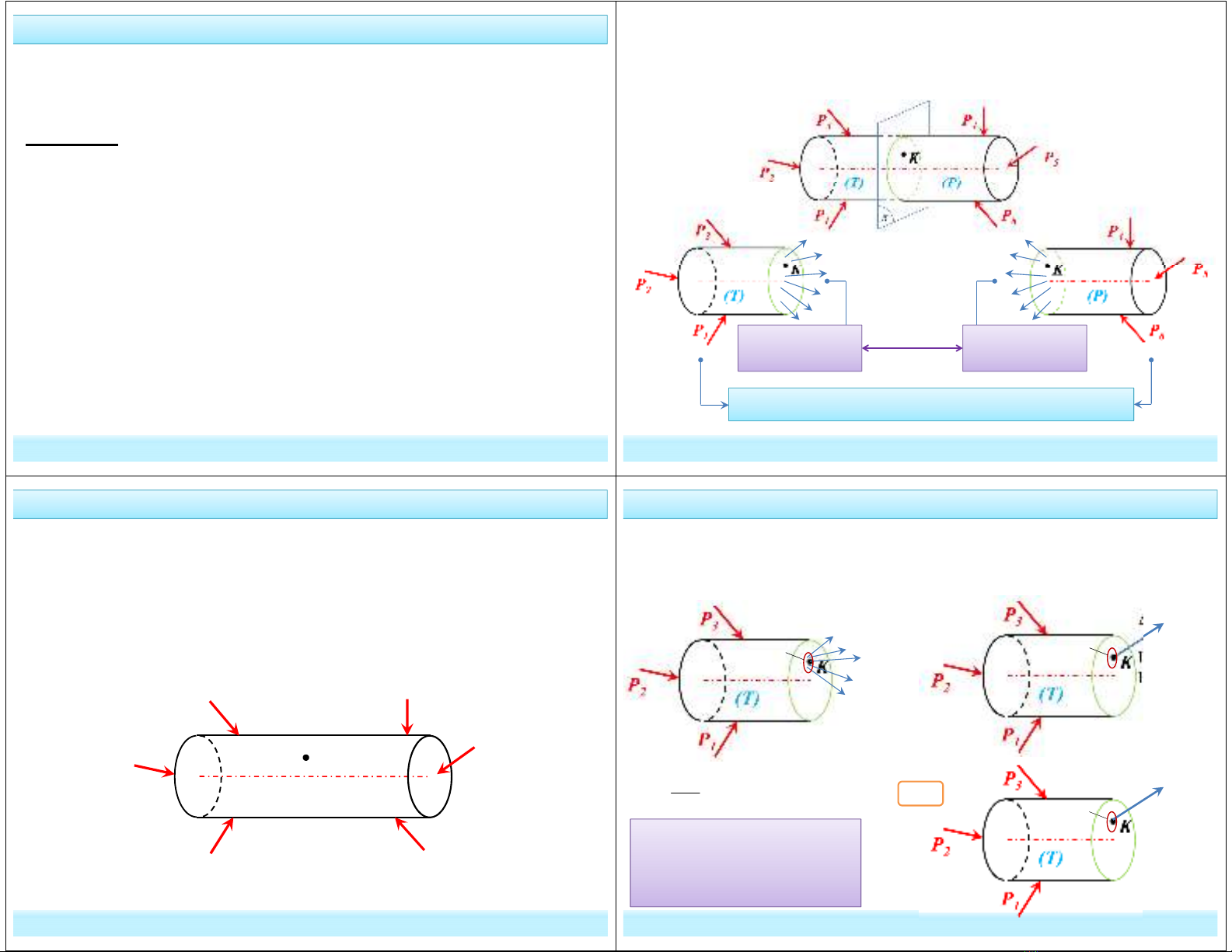
(C) : trục thanh; F: mặt cắt ngang (tiết diện)
+ Phân loại thanh: thẳng, cong, mcn không đổi, mcn thay đổi ...
a. Đặc trưng hình học của thanh: gồm trục thanh và mặt cắt ngang
+ Tổ hợp liên kết nhiều thanh: Khung (hệ thanh)
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bôSlide 1114
§2. Nội lực và phương pháp
mặt cắt ngang
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bô Slide 1115
1. Khái niệm về nội lực
* Nội lực: là lượng thay đổi của lực liên kết bên trong khi vật thể chịu
tác dụng của ngoại lực.
Lưu ý rằng: Khi nội lực đạt đến một giới hạn nào đó thì vật liệu bị phá
hoại. Vì vậy để đảm bảo vật thể không bị phá hoại thì nội lực không
thể lớn mãi mãi.
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bôSlide 1117
+ Nội dung phương pháp:
Tương hỗ
bằng nhau
Nội lực trên mcn
thuộc phần (T)
Nội lực trên mcn
thuộc phần (P)
Trên mỗi phần, nội lực cân bằng với ngoại lực
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bô Slide 1116
2. Phương pháp mặt cắt ngang
* Phương pháp mặt cắt ngang: là phương pháp để xác định nội lực
trên mặt cắt ngang của vật thể. Với đối tượng nghiên cứu là thanh, thì
với phương pháp này, ta hoàn toàn xác định được nội lực trên mặt cắt
ngang bất kỳ.
+ Yêu cầu bài toán: Xét thanh chịu tác dụng một hệ lực cân bằng sau,
xác định nội lực trên mcn chứa K.
K
P2
P3
P1
P4
P5
P6
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bôSlide 1118
a. Ứng suất tại một điểm
Ứng suất trung bình tại một điểm
Nội lực
trên
F
∆
F
∆
Hợp nội
lực trên
P
∆
∆
F
∆
Ứng suất
TB tại K
tb
p
F
∆
tb
P
p
F
∆
=
∆
: ứng suất TB tại K
Lượng thay đổi của lực
liên kết trung bình trên một
đơn vị diện tích thuộc ∆F.
3. Khái niệm về ứng suất
11.1
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bôSlide 1119
Ứng suất thực tại một điểm
Ứng suất
thực tại K
p
Lượng thay đổi của lực liên kết
tại chính điểm K xét trên mcn
Ứng suất là một đại lượng cơ
học đặc trưng cho mức độ chịu
đựng của vật liệu tại một điểm,
khi ứng suất đạt đến một giới
hạn nào đó thì vật liệu bị phá
hoại. Vì vậy việc xác định ứng
suất là cơ sở đánh giá mức độ
an toàn của vật liệu.
Phá
hoại
Phá
hoại
0
p
p
0
0
p p
<
0
p p
<
0
p p
=
0
p p
=
0
lim
F
P
p
F
∆ →
∆
=
∆

: ứng suất thực tại K 11.2
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bôSlide 1121
Quy ước dấu các thành phần ứng suất:
0
σ
>
0
τ
>
0
σ
>
0
τ
>
n
Pháp tuyến ngoài
'
n
Pháp tuyến ngoài
sau khi xoay
0
90
0
90
'
n
Pháp tuyến ngoài
sau khi xoay
n
Pháp tuyến ngoài
0
σ
>
: Khi cùng chiều với pháp tuyến ngoài ( hướng ra ngoài mcn) - gây kéo.
0
σ
<
: Khi ngược chiều với pháp tuyến ngoài ( hướng vào mcn) - gây nén.
0
τ
>
: Khi cùng chiều với pháp tuyến ngoài sau khi pháp tuyến ngoài xoay
900 thuận chiều kim đồng hồ. Chiều ngược lại là chiều âm.
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bô Slide 1120
b. Các thành phần ứng suất
p
K
P2
P3
P1
(T)
Phương trục thanh
thuộc mcn
σ
* Thành phần ứng suất pháp:
σ
τ
* Thành phần ứng suất tiếp:
τ
2 2
p
σ τ
= +
11.3
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bô Slide 1122
c. Phân tích ứng suất toàn phần trong hệ trục Cxyz.
(T)
P2
P3
P1
z
y
x
C
z
σ
zx
τ
zy
τ
K
2 2
p
σ τ
= +
z
σ σ
=
2 2 2
zx zy
τ τ τ
= +
2 2 2
z zx zy
p
σ τ τ
= + +
11.4