TS. Nguyeãn Thò Baûy - ÑHBK tp HCM -Baøi Giaûng CLC
ÑOÄNG LÖÏC HOÏC1
CHÖÔNG
V PHÖÔNG TRÌNH VI PHAÂN CHO CHAÁT LOÛNG LYÙ
TÖÔÛNG CHUYEÅN ÑOÄNG (P.Tr EULER)
dt
ud
)p(gradF
r
=
ρ
−1
⎪
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎪
⎬
⎫
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
==
∂
∂
ρ
−
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
==
∂
∂
ρ
−
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
==
∂
∂
ρ
−
⇔
)3(
z
u
u
y
u
u
x
u
u
t
u
dt
du
z
p1
F
)2(
z
u
u
y
u
u
x
u
u
t
u
dt
du
y
p1
F
)1(
z
u
u
y
u
u
x
u
u
t
u
dt
du
x
p1
F
z
z
z
y
z
x
zz
z
y
z
y
y
y
x
yy
y
x
z
x
y
x
x
xx
x
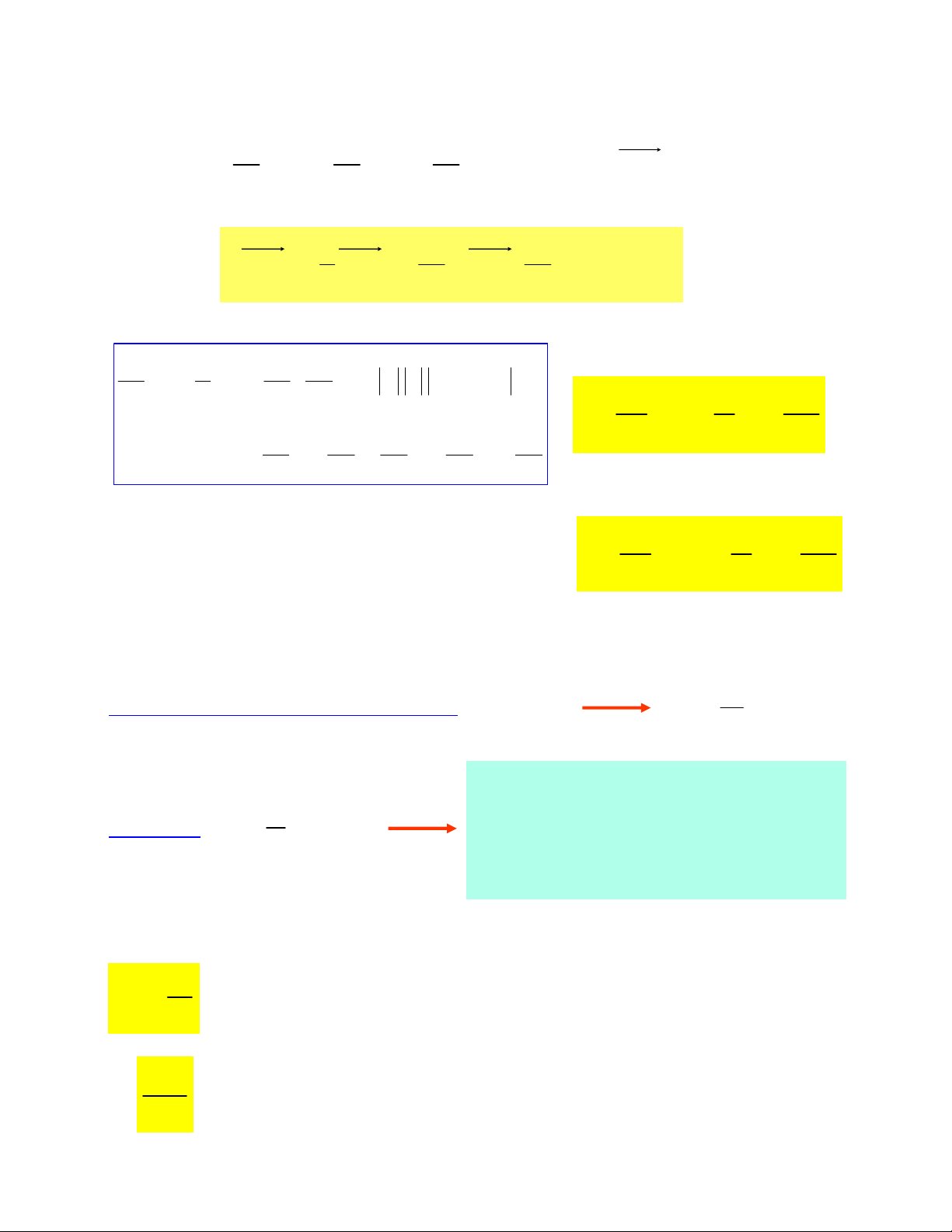
¾Daïng Lamb-Gromeco cuûa phöông trình Euler:
x
u
u
x
u
uz
z
y
y∂
∂
±
∂
∂
±vaø
zyyz
2
x
x
y
y
zx
z
2
z
2
y
2
xx
x
)u(rotu)u(rotu
2
u
xt
u
y
u
x
u
u
x
u
z
u
u
2
u
2
u
2
u
xt
u
x
p1
F
−+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
+
∂
∂
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
−
∂
∂
−
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
∂
∂
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛++
∂
∂
+
∂
∂
=
∂
∂
ρ
−
Sau khi saép xeáp, treân phöông x ta ñöôïc:
Ta bieán ñoåi töông töï cho p.tr (2) vaø (3).