Bài giảng Lý thuyết điều khiển tự động 2: Chương 7 - Đỗ Quang Thông

Chương 7<br /> PHÂN TÍCH CÁC HTĐKTĐ GIÁN ĐOẠN<br /> 7.1. TÍNH ỔN ĐỊNH CỦA CÁC HTĐKTĐ GIÁN<br /> ĐOẠN<br /> 7.1.1. Điều kiện cần và đủ để HTĐKTĐGĐ ổn<br /> định khi xét trên mặt phẳng s và mặt phẳng z<br /> Điều kiện ổn định của HTĐKTĐGĐ kín: nghiệm<br /> tự do (nghiệm riêng) của phương trình (đa thức)<br /> đặc trưng, hay quá trình quá độ của nó tắt dần<br /> theo thời gian.<br /> <br /> n<br /> <br /> y td (i ) =<br /> <br /> i<br /> ∑ Ak z k<br /> k =1<br /> <br /> i=0, 1, 2, 3, ...,<br /> <br /> (7.1)<br /> <br /> s<br /> kT 0<br /> =<br /> zk e<br /> là nghiệm phương trình (đa thức) đặc trưng của<br /> HTĐKTĐGĐ kín<br /> ( n −1)<br /> n<br /> (7.2)<br /> (<br /> )<br /> =<br /> +<br /> + ... 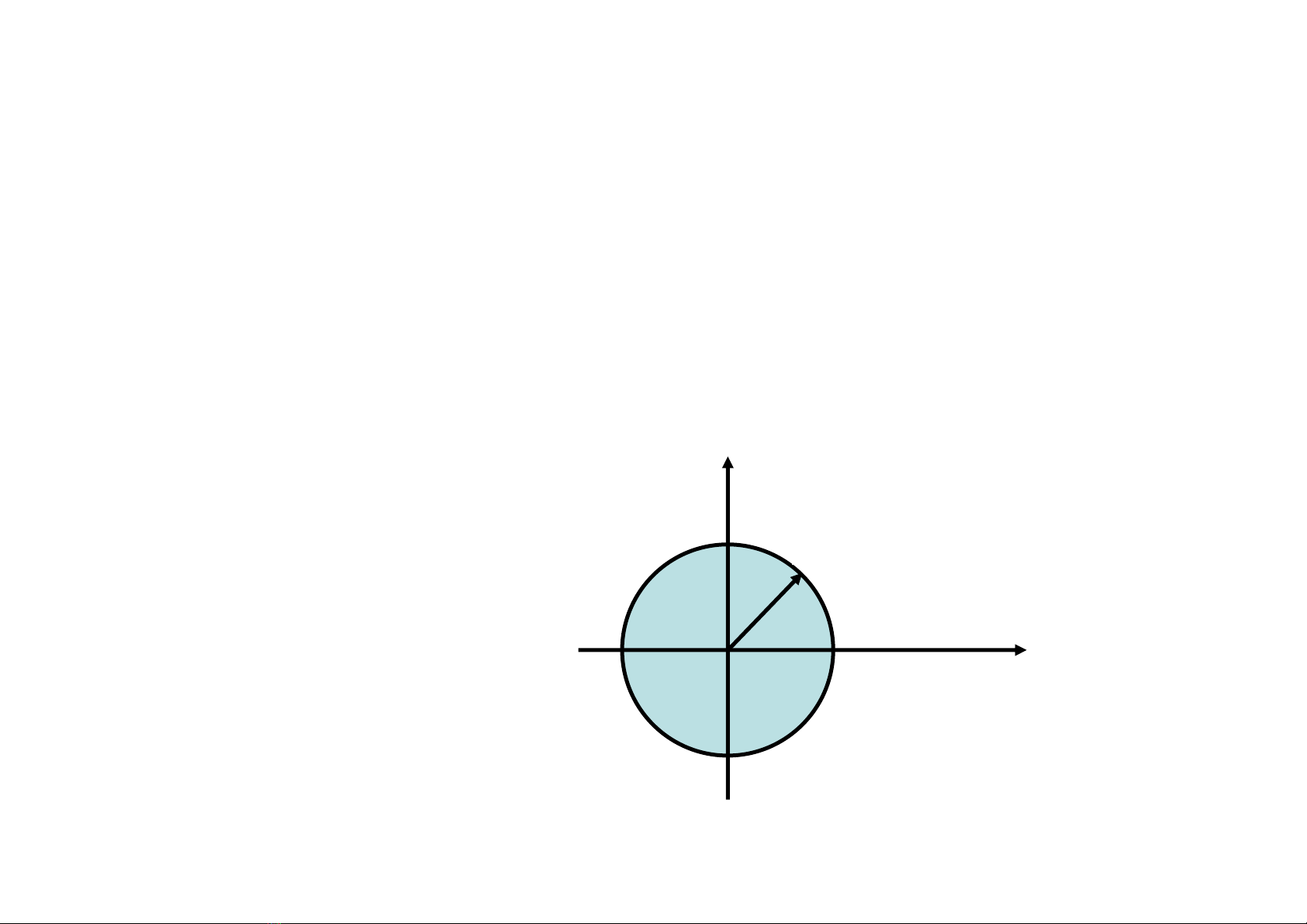+ d n = 0.<br /> D z d 0 z d1z<br /> <br /> Do<br /> <br /> i<br /> z k = e s k iT 0<br /> <br /> , nên suy ra rằng:<br /> <br /> - nếu sk nằm ở nửa trái của mặt phẳng phức s<br /> i<br /> thì z k sẽ tắt dần theo thời gian khi i→∞.<br /> - nếu tất cả các nghiệm sk nằm ở nửa trái của<br /> mặt phẳng phức s thì HT ổn định.<br /> <br /> Thay s=α±jω vào biểu thức của z, nhận được<br /> số phức z = e(α ± j ω ) T 0 . Với mỗi giá trị của tần số<br /> ω, số phức z được biểu diễn trên mặt phẳng<br /> phức z bằng một véc tơ có gốc nằm ở gốc toạ<br /> độ, ngọn có toạ độ tương ứng với phần thực và<br /> phần ảo của nó.<br /> jIm<br /> j1<br /> |z|=1<br /> ω=π/T0<br /> <br /> 0<br /> <br /> ω=0;<br /> ω=2π/T0<br /> <br /> 1<br /> <br /> Re<br /> <br /> Khi α=0, tức là z = e j ω T thì |z|=1. Vì vậy, trục ảo<br /> của mặt phẳng phức s tương ứng với đường<br /> tròn có tâm ở gốc toạ độ, bán kính đơn vị trên<br /> mặt phẳng phức z. Khi tần số ω thay đổi trong<br /> khoảng [0, 2π/T0] thì ngọn của véc tơ z quay một<br /> vòng trên đường tròn này.<br /> Thay s=-α±jω (với α>0) vào biểu thức của z,<br /> nhận được<br /> 0<br /> <br /> z<br /> <br /> = e −α T 0 ± j ωT 0 = e −α T 0 e ± j ω T 0 < 1.<br /> <br /> Vì vậy, nửa trái của mặt phẳng phức s tương<br /> ứng với phía trong đường tròn có tâm ở gốc toạ<br /> độ, bán kính đơn vị của mặt phẳng phức z.<br /> Thay s=α±jω (với α>0) vào biểu thức của z,<br /> nhận được<br /> <br /> z<br /> <br /> = eα T 0 ± j ωT 0 = eα T 0 e ± j ω T 0 > 1.<br /> <br /> Vì vậy, nửa phải của mặt phẳng phức s tương<br /> ứng với phía ngoài đường tròn có tâm ở gốc toạ<br /> độ, bán kính đơn vị của mặt phẳng phức z.<br /> <br />