BÀI GI NGẢ
BÀI GI NGẢ
TIN H C C SỌ Ơ Ở
TIN H C C SỌ Ơ Ở
BÀI 4. H Đ M Ệ Ế
N I DUNGỘ
N I DUNGỘ
H đ mệ ế
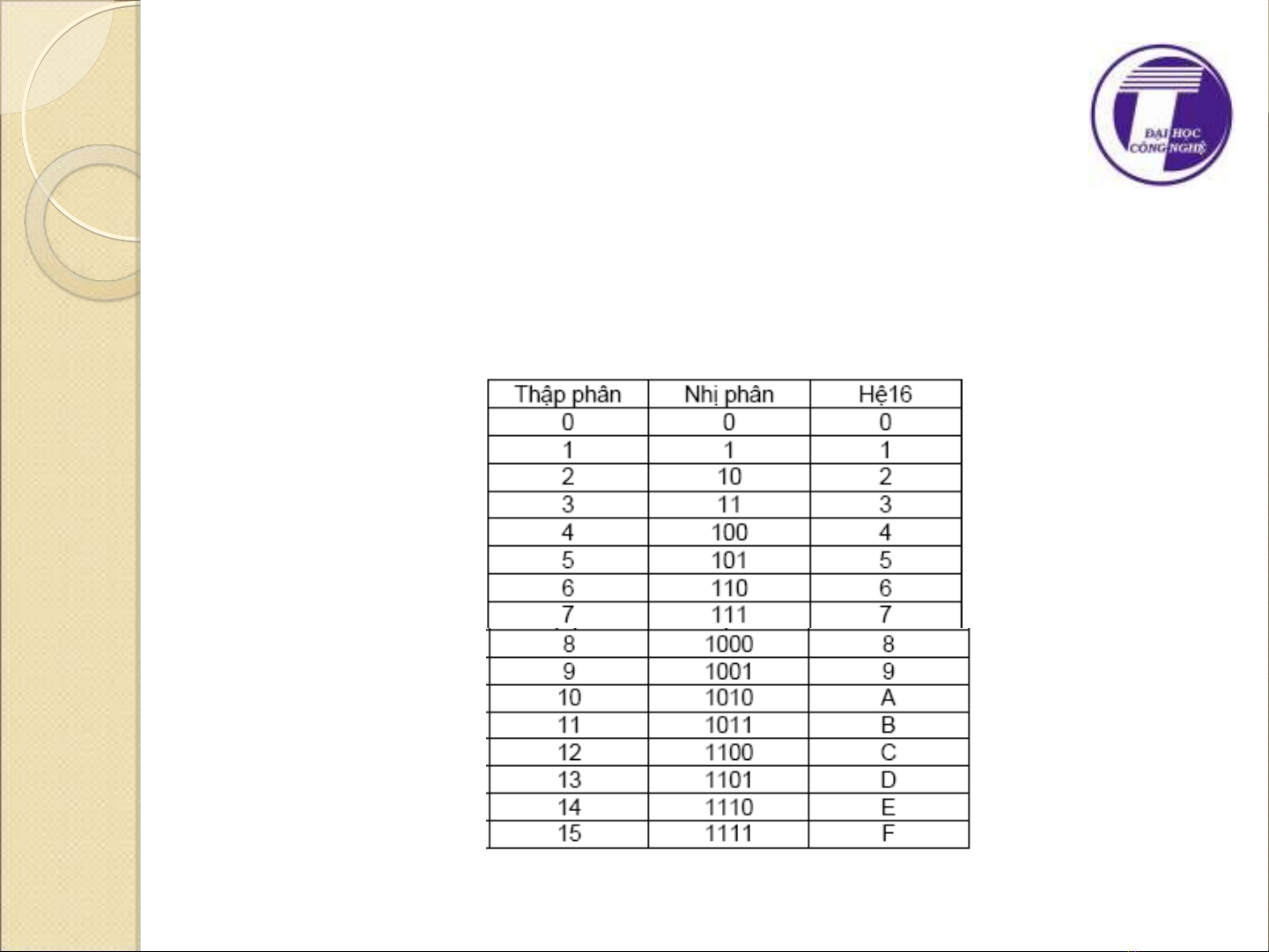
H đ m nh phân và h đ m c s 16ệ ế ị ệ ế ơ ố
Cách đ i bi u di n gi a các h đ mổ ể ễ ữ ệ ế
Đ i bi u di n gi a h nh phân và h ổ ể ễ ữ ệ ị ệ
đ m c s 16ế ơ ố
H Đ MỆ Ế
H Đ MỆ Ế
H đ m là m t t p các ký hi u (b ng ch s ) đ bi u ệ ế ộ ậ ệ ả ữ ố ể ể
di n các s và xác đ nh giá tr c a các bi u di n sôễ ố ị ị ủ ể ễ
H Đ M LA MÃỆ Ế
H Đ M LA MÃỆ Ế
H đ m La mãệ ế
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
N u m t ch s có m t ch s bên trái có giá tr nh h n thì giá tr c a ế ộ ữ ố ộ ữ ố ị ỏ ơ ị ủ
c p s b tình b ng hi u hai giá tr . Còn n u s có giá tr nh h n đ ng ặ ố ị ằ ệ ị ế ố ị ỏ ơ ứ
phía ph i thì giá tr chung b ng t ng hai giá tr . ả ị ằ ổ ị
MLVI = 1000 + 50 + 5 +1 =1056
MLIV = 1000 + 50 + 5 -1 = 1054
H Đ M TH P PHÂNỆ Ế Ậ
H Đ M TH P PHÂNỆ Ế Ậ
M i ch s x đ ng hàng th i tính t bên ph i có ỗ ữ ố ứ ở ứ ừ ả
giá tr là x.10 ịi-1. Nh v y m t đ n v m t hàng s ư ậ ộ ơ ị ở ộ ẽ
có giá tr g p 10 l n m t đ n v hàng k c n bên ị ấ ầ ộ ơ ị ở ế ậ
ph iả
Giá tr c a s là t ng giá tr c a các ch s có tính ị ủ ố ổ ị ủ ữ ố
t i v trí c a nó. Giá tr c a 3294,5 làớ ị ủ ị ủ
3.103 + 2.102 + 9.101 + 4.100 + 5.10-1