312
Ch¬ng 16
KHÔI PHỤC ẢNH
16.1. GIỚI THIỆU
Trong lịch sử, lĩnh vực hoạt động rộng lớn của xử lý ảnh số đã dành hết cho việc
khôi phục ảnh. Công việc này bao gồm cả nghiên cứu phát triển thuật giải lẫn
chương trình, xử lý ảnh có mục đích. Nhiều đóng góp đáng chú ý trong xử lý ảnh số
đã được thực hiện trước kia cũng như sau này.
Dựa vào khôi phục ảnh, chúng ta muốn loại bỏ hay làm giảm những suy giảm gặp
phải trong khi thu nhận ảnh số. Sự suy giảm bao gồm sự mờ do hệ thống quang học,
di chuyển đối tượng và cả nhiễu từ điện tử hay nguồn quang trắc. Trong khi khôi
phục ảnh có thể được định nghĩa bao gồm nhiều kỹ thuật đã đề cập trong Phần 1, ta
coi nó là biểu hiện của lớp các thao tác bị hạn chế nhiều hơn.
Tiêu chí cho việc khôi phục ảnh là mang lại một ảnh tương đối giống ảnh ban đầu
khi ảnh số thu được bị suy giảm. Mỗi phần tử trong chuỗi thu nhận ảnh (thấu kính,
film, bộ số hoá,...) đều có thể tạo ra suy giảm. Khôi phục từng phần ảnh bị mất chất
lượng có thể thoả mãn một khía cạnh thẩm mỹ nào đó, tuỳ thuộc vào từng ứng dụng
cụ thể. Một ví dụ cho trường hợp sau là các nhiệm vụ thu thập ảnh mặt trăng và hành
tinh trong chương trình không gian.
Trong chương này, chúng ta xem xét một vài phương pháp tiếp cận khôi phục
ảnh. Ta cũng xem xét các bài toán nhận biết hệ thống và mô phỏng nhiễu. Đối với
những tin tức chi tiết về các đối tượng, độc giả nên tham khảo tài liệu hay nghiên cứu
về lĩnh vực này.
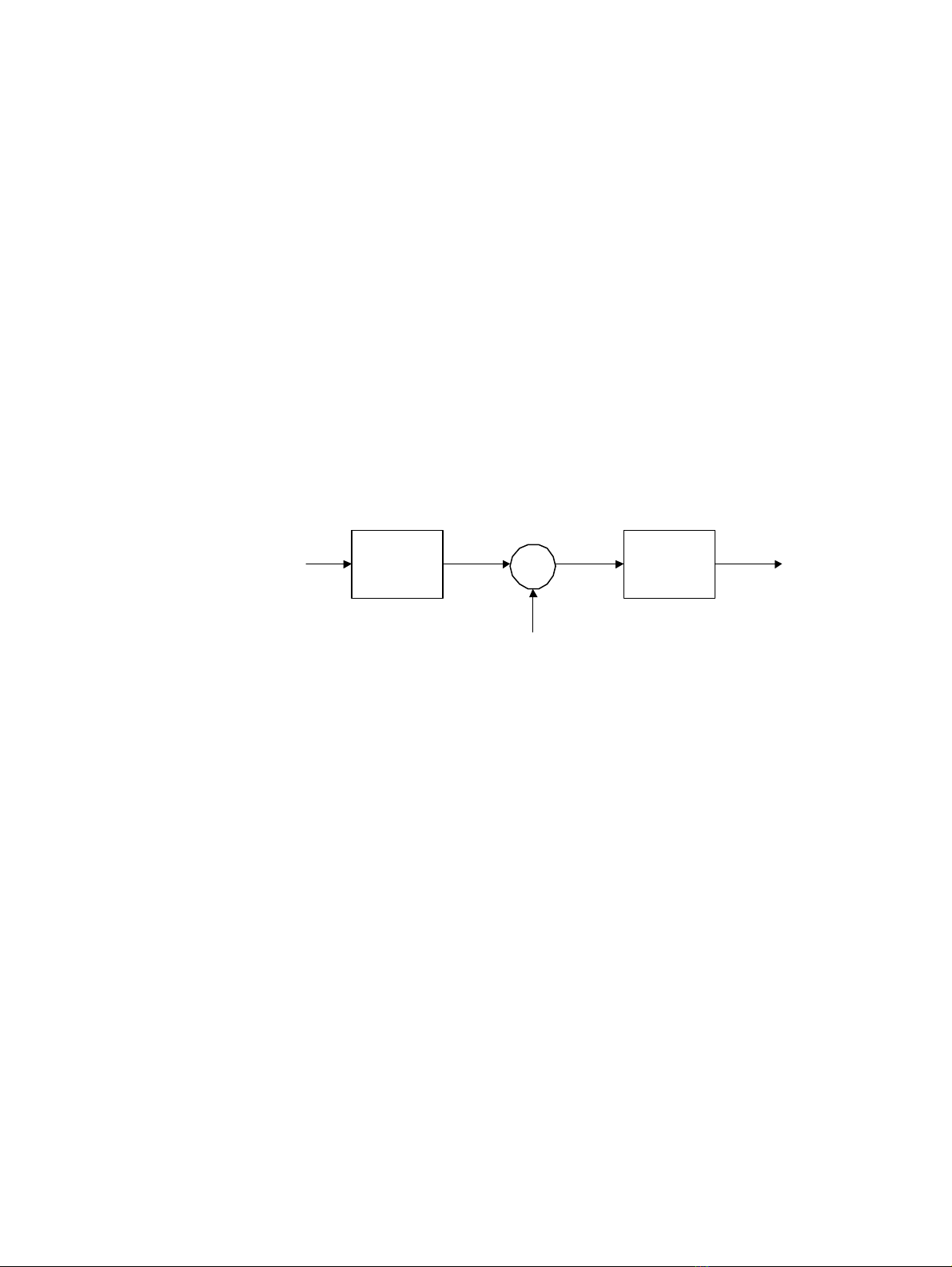
16.1.1. Tiếp cận và mô phỏng
Tiến trình khôi phục ảnh bị suy giảm có thể tiếp cận theo một trong hai cách cơ
bản. Nếu không biết nhiều về ảnh, ta có thể cố gắng để mô phỏng và mô tả đặc điểm
các nguồn suy giảm (mờ và nhiễu) và thực hiện quá trình loại bỏ và giảm bớt ảnh
hưởng của chúng. Đây là cách tiếp cận ước đoán, vì ta thử ước đoán ảnh như thế nào
trước khi bị suy giảm thông qua xử lý các đặc tính liên quan còn lại.
Nói cách khác, rất nhiều nhận thức trước đây về ảnh đã có sẵn, có thể thành công
hơn để phát triển mô hình toán học của ảnh ban đầu và điều chỉnh mô hình ảnh quan
sát. Một ví dụ cho trường hợp này, giả sử rằng ảnh đã biết chỉ chứa các đối tượng
hình tròn có kích thước cố định (các vì sao, các hạt, các tế bào,…). Ở đây, công việc
là sự phát hiện, vì chỉ một vài thông số của ảnh ban đầu là chưa biết (số lượng, vị trí,
biên độ,…).
Việc tiếp cận bài toán khôi phục ảnh cũng thể hiện ở một vài lựa chọn khác. Thứ
nhất, việc phát triển có thể sử dụng các phép toán rời rạc hay liên tục. Thứ hai, việc
phát triển có thể thực hiện trong miền không gian hay miền tần số. Cuối cùng, trong
khi việc thực hiện phải là số (digitally) thì khôi phục có thể thực hiện trong miền
không gian (qua tích chập) hay miền tần số (qua phép nhân).
Thật may mắn, bây giờ ta đã xác định đượ tập điều kiện mà, nếu được bảo toàn,
làm cho các phương pháp tiếp cận khác nhau đều cần thiết ngang nhau. Vì thế, chúng
313
ta có thể sử dụng bất cứ cách tiếp cận nào phù hợp với yêu cầu và ràng buộc của ta
nhất, miễn là chúng ta quan tâm đến những giả thiết cơ bản.
Thường thường, có hai hay nhiều cách tiếp cận đều dẫn đến cùng một kỹ thuật
khôi phục. Các phương pháp tiến hành tốt trong thực tiễn là cơ sở cho bài toán này.
Một trong số chúng luôn luôn có vẻ như chờ đợi ta cuối hành trình, không quan tâm
đến hướng ta xuất phát hay loại bản đồ và la bàn mà ta sử dụng.
Trong chương này, chúng ta xem xét một vài kỹ thuật khôi phục ảnh quan trọng.
Chúng ta bắt đầu bằng cách tiếp cận trong miền tần số liên tục theo thứ tự phát triển
và ứng dụng của chúng đối với ảnh số. Sau đó ta sẽ nghiên cứu trong miền không
gian rời rạc để thống nhất các kết quả có trước thành cơ cấu chung. Tiếp theo, chúng
ta sẽ xem xét khía cạnh thực tiễn của việc xử lý mờ biến thiên và nhiễu không cố
định. Sau khi xác định các tham số suy giảm ta tiến hành khôi phục ảnh.
16.2. CÁC BỘ LỌC KHÔI PHỤC ẢNH KINH ĐIỂN
Trong phần này, chúng ta sử dụng hệ thống trong Hình 16-1 để mô phỏng sự suy
giảm và khôi phục ảnh. Ảnh f(x,y) được làm mờ bằng phép toán tuyến tính h(x,y) và
nhiễu n(x,y) được thêm vào để tạo thành ảnh suy giảm w(x,y). Ảnh này được nhân
chập với bộ lọc khôi phục g(x,y) để cho ảnh khôi phục f^(x,y).
Hình 16-1 Mô hình khôi phục ảnh liên tục
Lý thuyết hệ thống tuyến tính đã được sử dụng để thiết kế các bộ lọc điện tử trong
nhiều năm trước khi xử lý ảnh trở nên phổ biến. Nó được ứng dụng rộng rãi trong
quang học, xử lý tín hiệu số và các lĩnh vực khác. Ví dụ, giải chập được biết đến
trong thiết kế bộ lọc điện tử và phân tích chuỗi thời gian. Thậm chí ước lượng sai số
bình phương trung bình (MSE) tối thiểu được Norbert Wienner trình bày vào năm
1948. Vì thế, nhiều kỹ thuật ứng dụng trong khôi phục ảnh là sự tổng hợp từ các
phương pháp một chiều đã sử dụng trong xử lý tín hiệu tương tự và tín hiệu số. Thậm
chí khi trở thành đặc trưng, các kỹ thuật mới đã được trình bày, chúng tập trung vào
cách tiếp cận miền tần số kinh điển
16.2.1. Giải chập (Deconvolution)
Vào giữa thập niên 60, giải chập (lọc ngược) đã bắt đầu được ứng dụng rộng rãi
để khôi phục ảnh số. Nathan đã sử dụng giải chập hai chiều để khôi phục ảnh từ các
nhiệm vụ thám hiểm hành tinh Ranger, Surveyor và Mariner. Vì phổ tín hiệu thường
tắt dần nhanh hơn nhiễu ở cùng tần số, nên các thành phần tần số cao thường bị
nhiễu tác động. Phương pháp tiếp cận của Nathan đã hạn chế hàm truyền đạt giải
chập xuống một giá trị tối đa nào đó (Hình 16-2).
Trong suốt chu kỳ lấy mẫu, Harris đã giải chập vệt mờ do sự hỗn loạn của bầu khí
quyển trong ảnh thiên văn sử dụng một mô hình phân tích đối với PSF và
McGlamery đã giải chập sự hỗn loạn khía quyển sử dụng một PSF xác định qua thực
nghiệm. Do đó, giải chập đã trở thành kỹ thuật tiêu chuẩn cho vấn đề khôi phục ảnh.
+
),( yxf ),( yxh ),( yxg
),( yxn
),( yxw ),(^ yxf
314
Hình 16-3 minh hoạ sự cải tiến có thể có trên ảnh khi kỹ thuật này được thực hiện
cẩn thận.
Hình 16-2 Giải chập
HÌNH 16-3
Hình 16-3 Giải chập ảnh Surveyor: (a)trước; (b) sau
16.2.2. Giải chập Wienner
Trong đa số các ảnh, các điểm ảnh liền kề rất tương quan với nhau, trong khi các
mức xám của các điểm ảnh riêng biệt chỉ tương quan lỏng lẻo. Từ đó, chúng ta có thể
chứng tỏ rằng hàm tự tương quan của ảnh đặc thù nói chung là suy giảm nhiều so với
ban đầu. Vì phổ năng lượng của ảnh là biến đổi Fourier (thực và chẵn) hàm tự tương
quan của nó nên chúng ta có thể chứng tỏ được rằng phổ năng lượng của một ảnh nói
chung suy giảm theo tần số.
Các nguồn nhiễu đặc trưng có phổ năng lượng bằng phẳng hoặc suy giảm theo tần
số chậm hơn so với phổ năng lượng của ảnh. Vì thế, trạng thái mong muốn là sao cho
1 1
15
hh
hh
(a) § ¸ p øng lý thuyÕt (b) § ¸p øng thùc tÕ
(c) § ¸ p øng ®o (d) § ¸p øng ®· hiÖu chØnh
0
0.2
1
315
phổ tín hiệu ở tần số thấp còn nhiễu chiếm các tần số cao. Bởi vì kích thước bộ lọc
giải chập thường tăng theo tần số nên bộ lọc sẽ tăng cường nhiễu tần số cao. Những
cố gắng vận dung giải chập bài toán nhiễu bằng các phương pháp đặc biệt và trực
quan.
Helstrom đã chấp nhận thủ tục ước lượng sai số bình phương trung bình và đã
trình bày bộ lọc giải chập Wienner, có hàm truyền đạt hai chiều
),(),(),(
),(),(
),( 2
*
vuPvuPvuH
vuPvuH
vuG
nf
f
(1)
và có thể viết lại như sau:
),(/),(),(
),(
),( 2
*
vuPvuPvuH
vuH
vuG
fn
(2)
trong đó Pf và Pn là phổ năng lượng của tín hiệu và nhiễu. Bộ lọc này được trình
bày trong chương 11 cho trường hợp một chiều.
Hình 16-4 Vấn đề nhiễu trong giải chập
Slepian đã mở rộng giải chập Wienner để giải thích PSF suy biến (ví dụ do nhiễu
loạn khí quyển). Sau đó, Pratt và Habibi đã phát triển công cụ để tăng hiệu quả tính
toán của giải chập Wienner.
s
s
s
s
s
Hµm tù t¬ng quan Phæ n¨ng lîng nhiÔu
Phæ n¨ng lîng Tû lÖ tÝn hiÖu/nhiÔu (SNR)
Phæ biªn ®é Bé läc gii chËp
)(
f
R)(sPn
)(sPf
)(
)(
sP
sP
n
f
)(sF
)(
1
sH
316
Giải chập Wienner tạo ra một phương pháp tối ưu cho việc thực hiện hàm truyền
đạt giải chập trong sự hiện diện của nhiễu, nhưng nó bị vướng mắc với ba vấn đề hạn
chế tính hiệu quả của nó. Thứ nhất, tiêu chuẩn sai số bình phương trung bình (MSE)
của sự tối ưu không đặc biết tốt nếu ảnh đang được khôi phục trong mắt người. Vấn
đề là ở chỗ tiêu chuẩn MSE xử lý mọi sai số như nhau, bất chấp vị trí của chúng
trong ảnh, trong khi mắt phải chịu đựng các sai số trong vùng tối và vùng gradient
cao nhiều hơn các hệ thống khác. rong việc tối thiểu hoá sai số bình phương trung
bình, bộ lọc Wienner cũng có xu hướng làm trơn ảnh nhiều hơn những gì mà mắt ưa
thích.
Thứ hai, giải chập Wienner cổ điển không thể vận dụng PSF có biến làm mờ
thuộc không gian. Điều này xuất hiện với sự hôn mê, chứng loạn thị, sự uốn cong
của trường thể hiện và với vệt mờ di chuyển trong khi quay.
Cuối cùng, kỹ thuật không thể vận dụng cho các trường hợp phổ biến của tín hiệu
và nhiễu dừng. Đa số các ảnh là không dừng, có các khu vực bằng phẳng rộng phân
biệt bởi sự chuyển tiếp dễ nhận thấy (biên). Hơn nữa, một vài nguồn nhiễu quan
trọng tuỳ thuộc rất nhiều vào mức xám cục bộ. Trong hai phần tiếp theo, ta sẽ xem
xét những cách thức thực hiện và cải tiến giải chập Wienner.
16.2.3. Cân bằng phổ năng lượng
Canon đã chứng minh bộ lọc khôi phục phổ năng lượng của ảnh bị suy giảm thành
biên độ ban đầu là
2/1
2),(),(),(
),(
),(
vuPvuPvuH
vuP
vuG
nf
f (3)
Giống như bộ lọc Wienner, bộ lọc cân bằng phổ năng lượng (Power Spectrum
Equalization-PSE) này không có pha (thực và chẵn). Nó thích hợp cho các hàm làm
mờ không pha hay pha được xác định bởi các phương pháp khác.
Điểm tương đồng giữa bộ lọc PSE (biểu thức (3)) và bộ lọc giải chập Wienner
(biểu thức (1)) là quá rõ ràng. Cả hai bộ lọc đều giảm xuống còn giải chập trực tiếp
trong tình trạng không nhiễu và cả hai cắt hoàn toàn trong tình trạng không có tín
hiệu. Tuy nhiên, bộ lọc PSE không cắt tại các vị trí 0 trong hàm truyền đạt làm mờ
F(u, v).
Khả năng khôi phục ảnh của bộ lọc PSE rất tốt và trong vài trường hợp bộ lọc
PSE có thể được ưa thích hơn giải chập Wienner. Đôi khi bộ lọc PSE còn được gọi là
bộ lọc đồng hình (homomorphic filter).
16.2.4. Các bộ lọc trung bình hình học
Xét hàm truyền đạt bộ lọc khôi phục được cho bởi
1
2
*
2
*
),(/),(),(
),(
),(
),(
),( vuPvuPvuH
vuH
vuH
vuH
vuG
fn
(4)
trong đó
và
là các hằng số thực dương. Bộ lọc này là sự khái quát của các bộ
lọc đã đề cập trước đây. Hàm truyền đạt được tham số hoá theo
và
. Chú ý, nếu
= 1 thì biểu thức (4) rút gọn thành bộ lọc giải chập. Hơn nữa, nếu
= 1/2 và
= 1,
thì nó sẽ trở thành bộ lọc PSE trong biểu thức (3).