Bài giảng môn học
Xử Lý Tín Hiệu Số
Giảng viên: Lã Thế Vinh
Email:
vinhlt@soict.hut.edu.vn
Chú ý: bài giảng có sử dụng các học liệu được cung cấp bởi Giảng viên
Lê Duy Minh, Trường Đại học Kỹ thuật Công nghiệp Thái Nguyên.
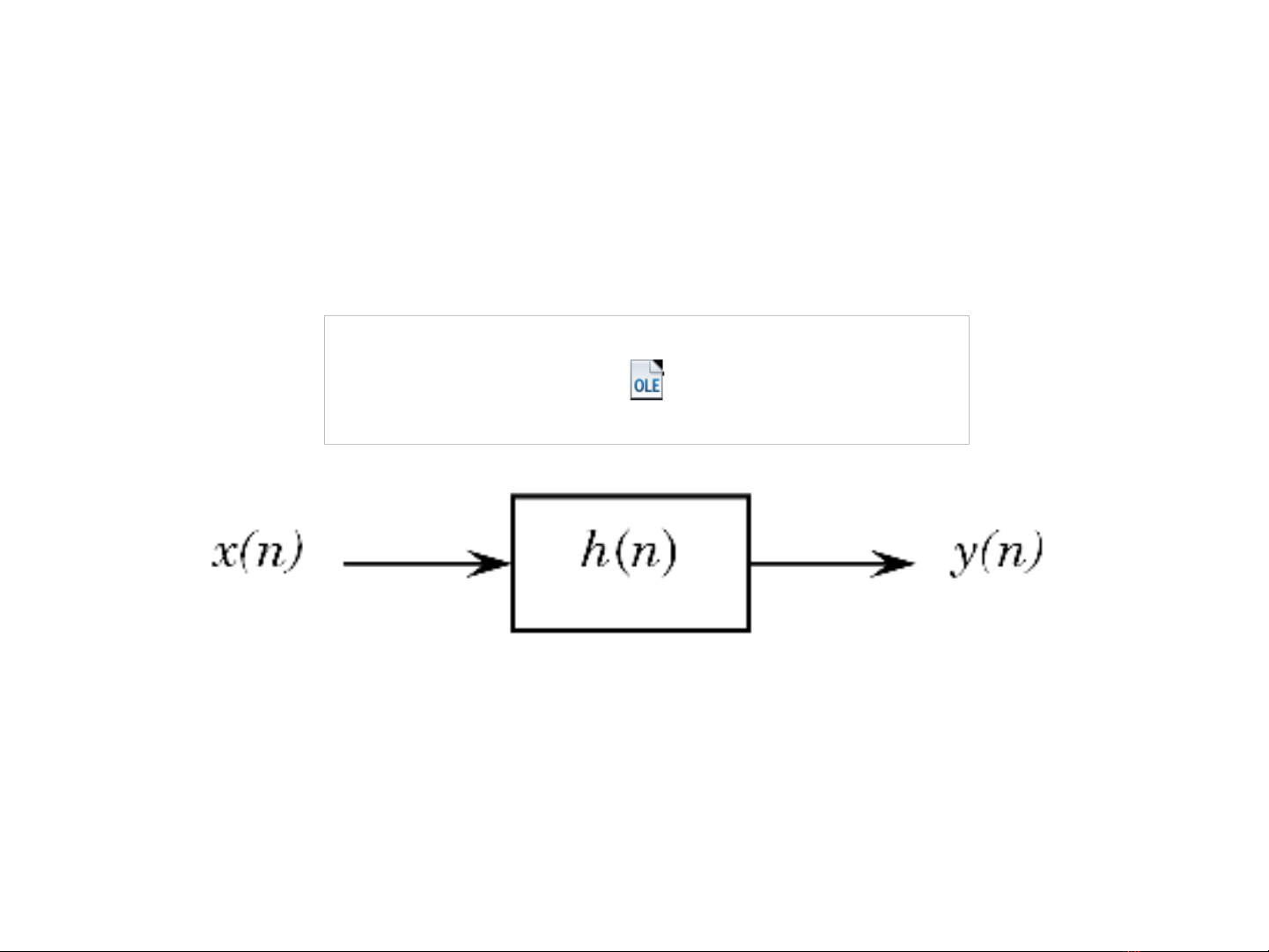
Tín hiệu và hệ thống rời rạc trên
miền thời gian
•Mọi tín hiệu x(n) có thể biểu diễn bởi:
•Từ đó ta có phương trình của hệ xử lý tín
hiệu
( ) ( ). ( )
k
k k
x n x n
δ
=−
= −
k
kk
nxFnxFny )()()]([)(
Tín hiệu và hệ thống rời rạc trên
miền thời gian
•Với giả thuyết hệ tuyến tính ta có
•Đặt
•Với hệ bất biến ta có
kk
kkkk
nhxnFxny ),().()]([.)()(
( ) [ ( )]h n F n
δ
=
( , ) ( )h n k h n k= −
Tín hiệu và hệ thống rời rạc trên
miền thời gian
•Do đó với hệ tuyến tính bất biến ta có:
•h(n) là đáp ứng xung của hệ TTBB
)()()().()( nx*nhnxhny
k
kk
Tín hiệu và hệ thống rời rạc trên
miền thời gian
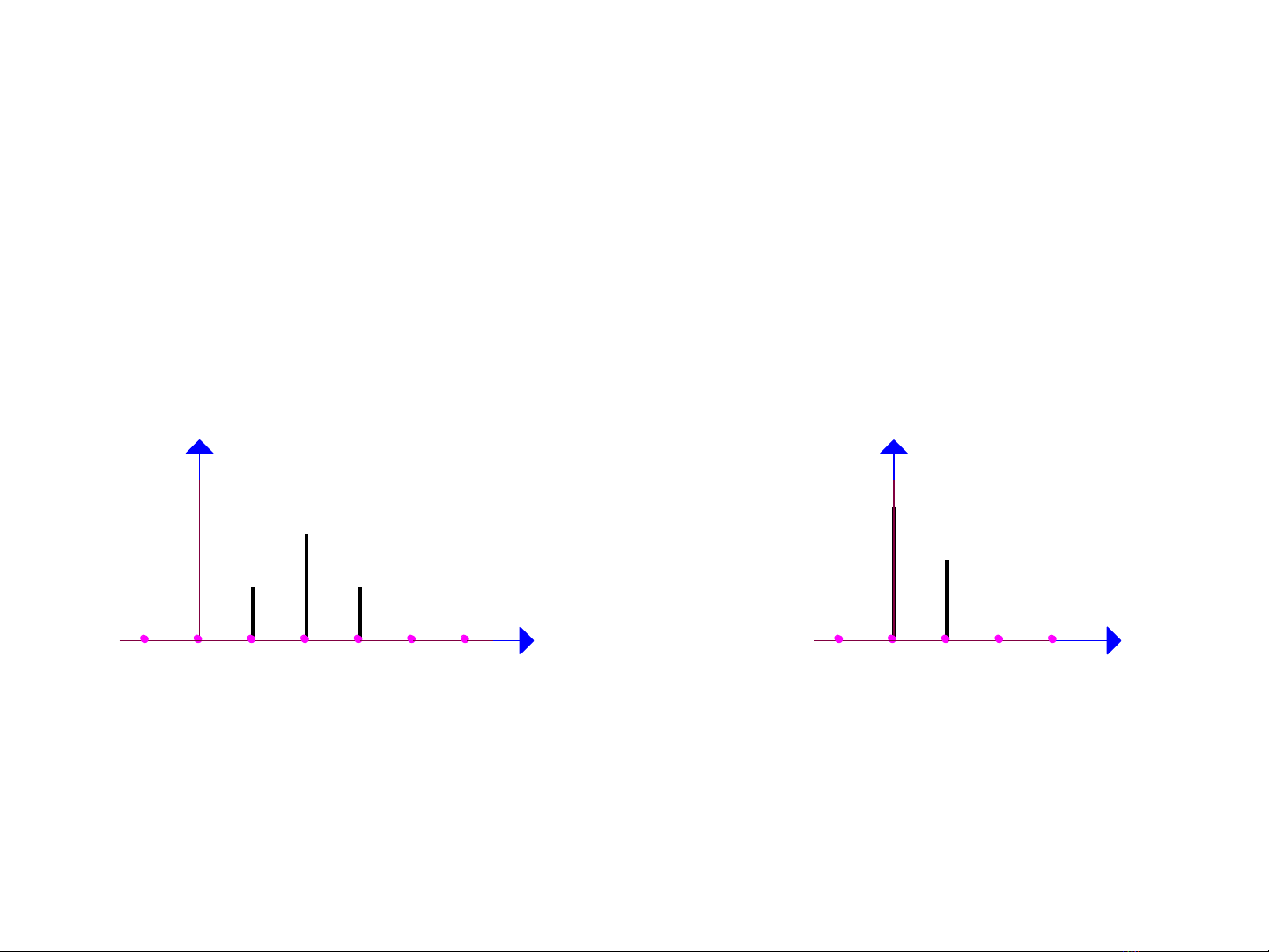
•Ví dụ 1: tính y(n) của hệ TTBB có đáp ứng
xung (trái) và tín hiệu vào như hình vẽ
3- 1 0 21
10 , 6
31 20- 1 4 5
0 , 4 0 , 4
0 , 8