BÀI 1: Đ I C NG V Đ NG TH NG VÀ M T PH NGẠ ƯƠ Ề ƯỜ Ẳ Ặ Ẳ
V n đ 1ấ ề : TÌM GIAO TUY N C A HAI M T PH NG Ế Ủ Ặ Ẳ α VÀ β :
Mu n tìm giao tuy n c a hai m t ph ng ố ế ủ ặ ẳ
α
và
β
ta đi tìm hai đi m chung I ; J c aể ủ
α
và
β
α
∩∪
β
= I J
Khi tìm đi m chung ta chú ý :ể
Cách g i tên hai m t ph ng đ phát hi n đi m chung ọ ặ ẳ ể ệ ể
M
∈
d và d
⊂
α
M
∈
α
β⊂α⊂
=∩
b;a
Mba (P) trong
M là đi m chung ể
1. 1: 1)Cho t di n ABCD có E là trung đi m c a AB. Hãy xác đ nh giao tuy nứ ệ ể ủ ị ế
c a m t ph ng (ECD) v i các m t ph ng (ABC) ; (ABD) ; (BCD) ; (ACD)ủ ặ ẳ ớ ặ ẳ
2)Cho t di n SABC và m t đi m I trên đo n SA; d là đ ng th ng trongứ ệ ộ ể ạ ườ ẳ
(ABC) c t AB; BC t i J ; K. Tìm giao tuy n c a m t ph ng (I,d) v i các m tắ ạ ế ủ ặ ẳ ớ ặ
ph ng sau : (SAB) ; (SAC) ; (SBC)ẳ
1. 2: 1)Cho t giác l i ABCD và đi m S không n m trong m t ph ng ch a t giác.ứ ồ ể ằ ặ ẳ ứ ứ
Tìm giao tuy n c a : ế ủ
a) (SAC) và (SBD) b) (SAB) và (SCD) c) (SAD) và
(SBC)
2)Cho hình chóp S.ABCDE. Hãy xác đ nh giao tuy n c a m t ph ng (SAC)ị ế ủ ặ ẳ
v i các m t ph ng (SAD) ; (SCE) ớ ặ ẳ
1. 3: Cho hình chóp S.ABCD có đáy ABCD là m t t giác l i ; M là đi m trên c nhộ ứ ồ ể ạ
CD. Tìm giao tuy n c a các m t ph ng : ế ủ ặ ẳ
a)(SAM) và (SBD) b)(SBM) ; (SAC)
1. 4: Cho t di n ABCD; M là đi m n m trong ứ ệ ể ằ ∆ABC; N là đi m n m trong ể ằ ∆ACD.
Tìm giao tuy n c a : a) (AMN) và (BCD)ế ủ b) (CMN) và (ABD)
1. 5: Cho t di n ABCD .M n m trên AB sao cho AM = ứ ệ ằ
4
1
MB ; N n m trên ACằ
sao cho AN = 3NC; đi m I n m trong ể ằ ∆BCD. Tìm giao tuy n c a : ế ủ
a) (MNI) và (BCD) b) (MNI) và (ABD) c) (MNI) và (ACD)
1. 6: Cho t di n ABCD ; g i I ; J l n l t là trung đi m c a AD; BC . ứ ệ ọ ầ ượ ể ủ
a) Tìm giao tuy n c a : (IBC) và (JAD)ế ủ
b)M là đi m trên AB; N là đi m trên AC. Tìm giao tuy n c a (IBC) và (DMN)ể ể ế ủ
1. 7: Cho hai đ ng th ng a ; b ườ ẳ ∈ (P) và đi m S không thu c (P). Hãy xác đ nh giaoể ộ ị
tuy n c a m t ph ng ch a a và S v i m t ph ng ch a b và S ?ế ủ ặ ẳ ứ ớ ặ ẳ ứ
1. 8: Cho t di n ABCD ; trên AB ; AC l n l t l y hai đi m M và N sao cho :ứ ệ ầ ượ ấ ể
NC
AN
MB
AM ≠
. Tìm giao tuy n c a (DMN) và (BCD)ế ủ
1. 9; Cho b n đi m ABCD không đ ng ph ng ; g i I ; K là trung đi m AD ; BC .ố ể ồ ẳ ọ ể
Xác đ nh giao tuy n c a hai m t ph ng (IBC) và (KAD) ?ị ế ủ ặ ẳ
1. 10 : Trong m t ph ng ặ ẳ α cho hình thang ABCD có đáy là AB ; CD ; S là đi mể
n m ngoài m t ph ng hình thang. Tìm giao tuy n c a : ằ ặ ẳ ế ủ
a) (SAD) và (SBC) b) (SAC) và (SBD)
α
β
I
J
•
•
1.11. Hình chóp S.ABCD có đáy ABCD là hình thang hai đáy là AD ; BC .G i M ; Nọ
là trung đi m AB ; CD và G là tr ng tâm ể ọ ∆SAD. Tìm giao tuy n c a :ế ủ
a) (GMN) và (SAC) b) (GMN) và (SBC)
V n đ 2:ấ ề CH NG MINH BA ĐI M TH NG HÀNG Ứ Ể Ẳ
VÀ BA Đ NG TH NG Đ NG QUY ƯỜ Ẳ Ồ
Ch ng minh A; B; C th ng hàngứ ẳ :
Ch ra A ; B ; C ỉ
∈
α
Ch ra A ; B ; C ỉ
∈
β
K t lu n : A; B; Cế ậ
∈
α
∩∪
β
A; B; C th ng hàng ẳ
Ch ng minh a ; b ; MN đ ng quyứ ồ :
Đ t a ặ
∪∩
b = P
Ch ng minh M ; N ; P th ng hàng ứ ẳ
K t lu n :MN ; a ; b đ ng quy t i P ế ậ ồ ạ
2. 1: Cho hai m t ph ng ặ ẳ α và β c t nhau theo giao tuy n d .Trên ắ ế α l y hai đi m A ;ấ ể
B nh ng không thu c d. O là đi m ngoài hai m t ph ng . Các đ ng th ng OA ;ư ộ ể ở ặ ẳ ườ ẳ
OB l n l t c t ầ ượ ắ β t i A’ ; B’. AB c t d t i Cạ ắ ạ
a)Ch ng minh O; A; B không th ng hàng ?ứ ẳ
b)Ch ng minh A’ ; B’ ; C’ th ng hàng ? T đó suy ra AB ; A’B’; d đ ng quyứ ẳ ừ ồ
2. 2: Trong không gian cho ba tia Ox ; Oy ; Oz không đ ng ph ng. Trên Ox l y A ;ồ ẳ ấ
A’ ; trên Oy l y B ; B’ trên Oz l y C ; C’ sao cho AB c t A’B’ t i D ; BC c t B’C’ấ ấ ắ ạ ắ
t i E ; AC c t A’C’ t i F. Ch ng minh D; E ; F th ng hàng ?ạ ắ ạ ứ ẳ
2. 3: Cho A; B; C không th ng hàng ngoài m t ph ng ẳ ở ặ ẳ α . G i M ; N ; P l n l tọ ầ ượ
là giao đi m AB ; BC ; AC v i ể ớ α. Ch ng minh M; N; P th ng hàng ?ứ ẳ
2. 4: 1) Cho hình chóp S.ABCD đáy ABCD là hình bình hành ; O là giao đi m haiể
đ ng chéo ; M ; N l n l t là trung đi m SA ; SD. Ch ng minh ba đ ng th ngườ ầ ượ ể ứ ườ ẳ
SO ; BN ; CM đ ng quy ồ
2)Cho t di n ABCD.M t ph ng ứ ệ ặ ẳ α không song song AB c t AC ; BC ; AD ;ắ
BD l n l t t i M ; N ; R ; S . Ch ng minh AB ; MN ; RS đ ng quy ?ầ ượ ạ ứ ồ
2. 5: Ch ng minh trong m t t di n các đ ng th ng n i đ nh v i tr ng tâm m tứ ộ ứ ệ ừơ ẳ ố ỉ ớ ọ ặ
đ i di n đ ng quy ?ố ệ ồ
2.6. Hình chóp S.ABCD có đáy ABCD là hình thang hai đáy là AD ; BC .G i M ; Nọ
là trung đi m AB ; CD và G là tr ng tâm ể ọ ∆SAD. Tìm giao tuy n c a :ế ủ
a) (GMN) và (SAB) b) (GMN) và (SCD)
c) G i giao đi m c a AB và CD là I ; J là giao đi m c a hai giao tuy n c a câu aọ ể ủ ể ủ ế ủ
và câu b. Ch ng minh S ; I ; J th ng hàng ?ứ ẳ
α
β
A
C
•
•
•
B
N
•
•
a
b
P
V n đ 3: ấ ề CH NG MINH HAI Đ NG TH NG CHÉO NHAU,Ứ ƯỜ Ẳ
VÀ CÁC ĐI M Đ NG PH NGỂ Ồ Ẳ
Ch ng minh 2 đ ng th ng a ; b chéo nhauứ ườ ẳ :
Gi s : a không chéo b ả ử
T đó suy ra hai đ ng th ng a và b n m trong ừ ườ ẳ ằ
cùng m t ph ng ặ ẳ
α
( đ ng ph ng )ồ ẳ
T đó suy ra đi u mâu thu n v i g a thi t ho c ừ ề ẫ ớ ỉ ế ặ
mâu thu n v i m t đi u đúng nào đó ẫ ớ ộ ề
Ch ng minh A, B, C, D n m trong cùng m t m t ph ng – đ ng ph ngứ ằ ộ ặ ẳ ồ ẳ
Ch ng minh hai đ ng ứ ườ
th ng t o thành t b n ẳ ạ ừ ố
đi m đó c t nhau ho c ể ắ ặ
song song v i nhauớ
3. 1: Cho b n đi m A, B, C, D không đ ng ph ng ố ể ồ ẳ
a)Ch ng minh ba trong s 4 đi m này không th ng hàng ứ ố ể ẳ
b)Ch ng minh AB chéo v i CD ?ứ ớ
3. 2: Cho hai đ ng th ng chéo nhau a và b.Trên a l y hai đi m A, B ; trên b l yườ ẳ ấ ể ấ
hai đi m C, Dể
a)Ch ng minh AC chéo BD ?ứ
b)L y M n m trên đo n AC; N n m trên đo n BD. Đ ng th ng MN có song songấ ằ ạ ằ ạ ườ ẳ
AB ho c CD không ?ặ
c)O là trung đi m MN. Ch ng minh A, O, C, N đ ng ph ng ể ứ ồ ẳ
3. 3: Cho đ ng th ng a c t hai đ ng th ng b và c. H i ba đ ng th ng a, b, c cóườ ẳ ắ ườ ẳ ỏ ườ ẳ
đ ng ph ng không ? T i sao ?ồ ẳ ạ
3. 4: Cho t di n ABCD. G i I ; J là trung đi m AD; BC. ứ ệ ọ ể
a) Ch ng minh AB chéo CD ?ứb) Ch ng minh IB chéo JA ?ứ
V n đ 4:ấ ề TÌM GIAO ĐI M C A Đ NG TH NG D VÀ M T PH NG Ể Ủ ƯỜ Ẳ Ặ Ẳ α
Gi s ph i tìm giao đi m d ả ử ả ể ∩ α = ?
Ph ng pháp 1: ươ
Tìm a
⊂
α
Ch ra đ c a ,d n m trong cùng m t ph ng và ỉ ượ ằ ặ ẳ
chúng c t nhau t i M ắ ạ
d
∩∪
α
= M ( hình v )ẽ
Ph ng pháp 2: ươ
Tìm
β
ch a d thích h p ứ ợ
Gi i bài toán tìm giao tuy n a c a ả ế ủ
α
và
β
b
a
α
•
A
α
B
C
D
•
•
•
•
A
α
B
C
D
•
•
•
•
α
d
a
M
•
α
M
β
d
a
Trong
β
: a
∪∩
d = M
d
∪
α
= M ( hình v b)ẽ
4. 1: Cho t di n SABC; M ; N l n l t là các đi m n m trong ứ ệ ầ ượ ể ằ ∆SAB ; ∆SBC. MN
c t (ABC) t i P. Xác đ nh giao đi m Pắ ạ ị ể
4. 2: Cho t di n ABCD ; M là trung đi m AB; N và P l n l t là các đi m n mứ ệ ể ầ ượ ể ằ
trên AC; AD sao cho AN : AC = 3 : 4 ; AP : AD = 2 : 3. Tìm giao đi m :ể
a) MN v i (BCD)ớb) BD v i (MNP)ớ
c) G i Q là trung đi m NP.Tìm giao đi m c a MQ v i (BCD)ọ ể ể ủ ớ
4. 3: A; B ; C ; D là b n đi m không đ ng ph ng. M; N l n l t là trung đi m c aố ể ồ ẳ ầ ượ ể ủ
AC; BC. Trên đo n BD l y P sao cho BP = 2PD. Tìm giao đi m c a :ạ ấ ể ủ
a) CD v i (MNP)ớb) AD v i (MNP)ớ
4. 4: Cho hình chóp SABC ; O là đi m trong ể∆ABC ; D và E là các đi m năm trênể
SB ; SC.Tìm giao đi m c a a) DE v i (SAO)ể ủ ớ b) SO v i (ADE)ớ
4. 5: Cho t di n SABC. I ; H l n l t là trung đi m SA; AB. Trên đo n SC l yứ ệ ầ ượ ể ạ ấ
đi m K sao cho CK = 3KS.ể
a)Tìm giao đi m c a đ ng th ng BC v i (IHK) ?ể ủ ườ ẳ ớ
b)G i M là trung đi m HI. Tìm giao đi m c a đ ng th ng KM v i (ABC) ?ọ ể ể ủ ườ ẳ ớ
4. 6: Cho hình chóp SABCD đáy là hình thang ABCD đáy l n AB. I; J; K là baớ
đi m trên SA; SB; SC .Tìm giao đi m IK và (SBD); giao đi m ( JK) và SD; SCể ể ể Ị
4. 7: G i I ; J l n l t là hai đi m n m trong ọ ầ ượ ể ằ ∆ABC; ∆ABD c a t di n ABCD. Mủ ứ ệ
là đi m tuỳ ý trên CD. Tìm giao đi m IJ và m t ph ng (AMB) ể ể ặ ẳ
4. 8: Hình chóp SABCD đáy là hình bình hành ABCD. M là trung đi m SDể
a)Tìm giao đi m I c a BM và (SAC) ? ể ủ Ch ng minh : BI = 2IM ?ứ
b)Tìm giao đi m J c a c a SA và (BCM) ? Ch ng minh J là trung đi m SA ?ể ủ ủ ứ ể
c) N là đi m tuỳ ý trên BC. Tìm giao đi m c a MN v i (SAC) ?ể ể ủ ớ
V n đ 5:ấ ề THI T DI N T O B I M T PH NGẾ Ệ Ạ Ở Ặ Ẳ α V I KH I ĐAỚ Ố
DI NỆ
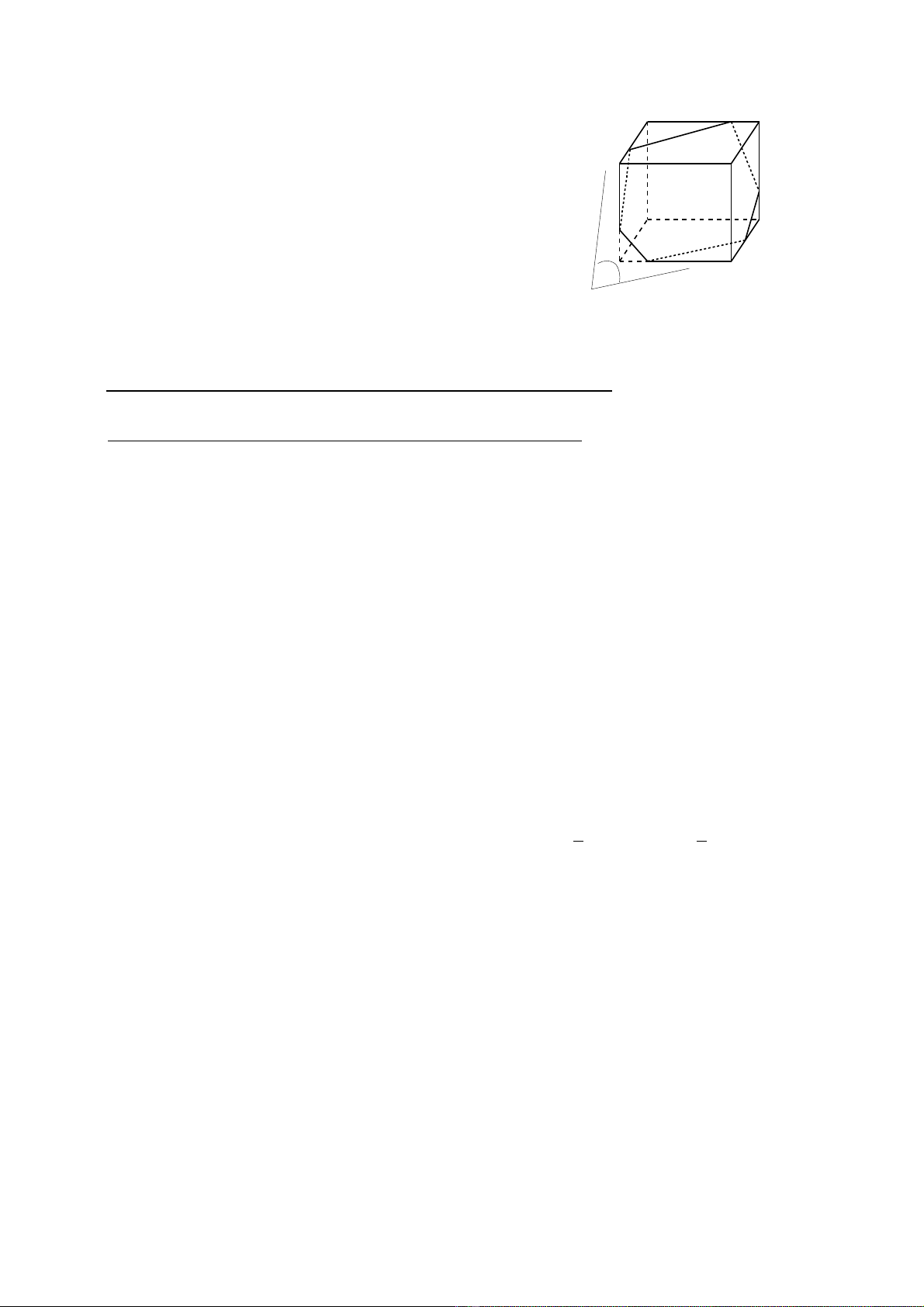
L n l t xét giao tuy n c a ầ ượ ế ủ
α
v i các ớ
m t c a kh i đa di n đ ng th i xét giao đi m c a ặ ủ ố ệ ồ ờ ể ủ
các c nh c a đa di n v i m t ph ng ạ ủ ệ ớ ặ ẳ
α
Khi các đo n giao tuy n tìm đ c khépạ ế ượ
kín thành đa giác ta đ c thi t di n ph i tìm.ượ ế ệ ả
Vi c ch ng minh ti t di n có hình ệ ứ ế ệ
d ng đ c bi t nh hình bình hành; hình thang ; ạ ặ ệ ư
. . . trong m t ph ng ặ ẳ
α
cũng nh vào quá trình ờ
đi tìm giao tuy n và giao đi m trên ế ể ở
Trong ph n này ta ch xét hai cách làm c b n :ầ ỉ ơ ả
I. Xác đ nh thi t di n b ng cách kéo dài các giao tuy nị ế ệ ằ ế
II.Xác đ nh thi t di n b ng cách v giao tuy n phị ế ệ ằ ẽ ế ụ
5. 1: 1) Cho hình l p ph ng ABCDA’B’C’D’. G i M ; N ; P l n l t là trungậ ươ ọ ầ ượ
đi m AA’ ; AD ; DC . Tìm thi t di n t o b i m t ph ng đi qua M; N; P v i hìnhể ế ệ ạ ở ặ ẳ ớ
l p ph ng ?ậ ươ
2) Cho hình h p ABCDA’B’C’D’. G i M ; N ; P l n l t là trung đi m DC ;ộ ọ ầ ượ ể
AD ; BB’. Tìm thi t di n t o b i m t ph ng (MNP) v i hình h p và giao tuy nế ệ ạ ở ặ ẳ ớ ộ ế
c a (MNP) v i m t ph ng (A’B’C’D’)ủ ớ ặ ẳ
5. 2: 1)Cho hình chóp S.ABCD đáy ABCD là hình bình hành . G i E; F; K l n l tọ ầ ượ
là trung đi m c a SA ; AB ; BC. Xác đ nh thi t di n c a hình chóp và m t ph ngể ủ ị ế ệ ủ ặ ẳ
đi qua ba đi m E; F ; Kể
2) Cho hình chóp S.ABCD. G i A’ ; B’ ; C’ l n l t là các đi m n m trênọ ầ ượ ể ằ
SA ; SB; SC. Xác đ nh thi t di n t o b i m t ph ng (A’B’C’) v i hình chópị ế ệ ạ ở ặ ẳ ớ
*5. 3: Cho t di n ABCD ; đi m I n m trên BD và ngoài BD sao cho ID = 3IB;ứ ệ ể ằ ở
M ; N là hai đi m thu c c nh AD ; DC sao cho MA = ể ộ ạ
2
1
MD ; ND =
2
1
NC
a)Tìm giao tuy n PQ c a (IMN) v i (ABC) ?ế ủ ớ
b)Xác d nh thi t di n t o b i (IMN) v i t di n ?ị ế ệ ạ ở ớ ứ ệ
c)Ch ng minh MN ; PQ ; AC đ ng qui ?ứ ồ
*5. 4: 1)Cho t di n ABCD ; đi m I ; J l n l t là tr ng tâm ứ ệ ể ầ ượ ọ ∆ABC ; ∆DBC ; M là
trung đi m AD. Tìm ti t di n t o b i (MJI) và t di n ?ể ế ệ ạ ở ứ ệ
2) Cho hình chóp S.ABCDE. L y ba đi m M ; N ; K trên SA ; BC ; SD. Xácấ ể
đ nh thi t di n t o b i m t ph ng (MNK) v i hình chóp ị ế ệ ạ ở ặ ẳ ớ
5. 5: Hình chóp SABCD có đáy ABCD là hình thang v i AB là đáy . G i M ; N làớ ọ
trung đi m SB ; SC .ể
a)Tìm giao tuy n c a (SAD) và (SBC) ?ế ủ
b)Tìm giao đi m c a SD v i m t ph ng (AMN) ?ể ủ ớ ặ ẳ
c)Tìm ti t di n t o b i m t ph ng (AMN) v i hình chóp ế ệ ạ ở ặ ẳ ớ
A
α
B
D
C
E
F