Uoán phaúng thanh thaúng Khoa Xaây Döïng & Cô Hoïc ÖÙng Duïng
Baøi taäp söùc beàn vaät lieäu trang 1 05/2013
Chöông 05
UOÁN PHAÚNG THANH THAÚNG
I. TOÙM TAÉT LYÙ THUYEÁT
1.1 Thanh chòu uoán thuaàn tuùy
Toàn taïi duy nhaát moät thaønh phaàn noäi löïc treân maët caét ngang, moâ men uoán
x
M
.
Qui öôùc daáu cuûa moâmen uoán: moâmen uoán ñöôïc goïi laø döông khi laøm caêng phaàn
beân döôùi.
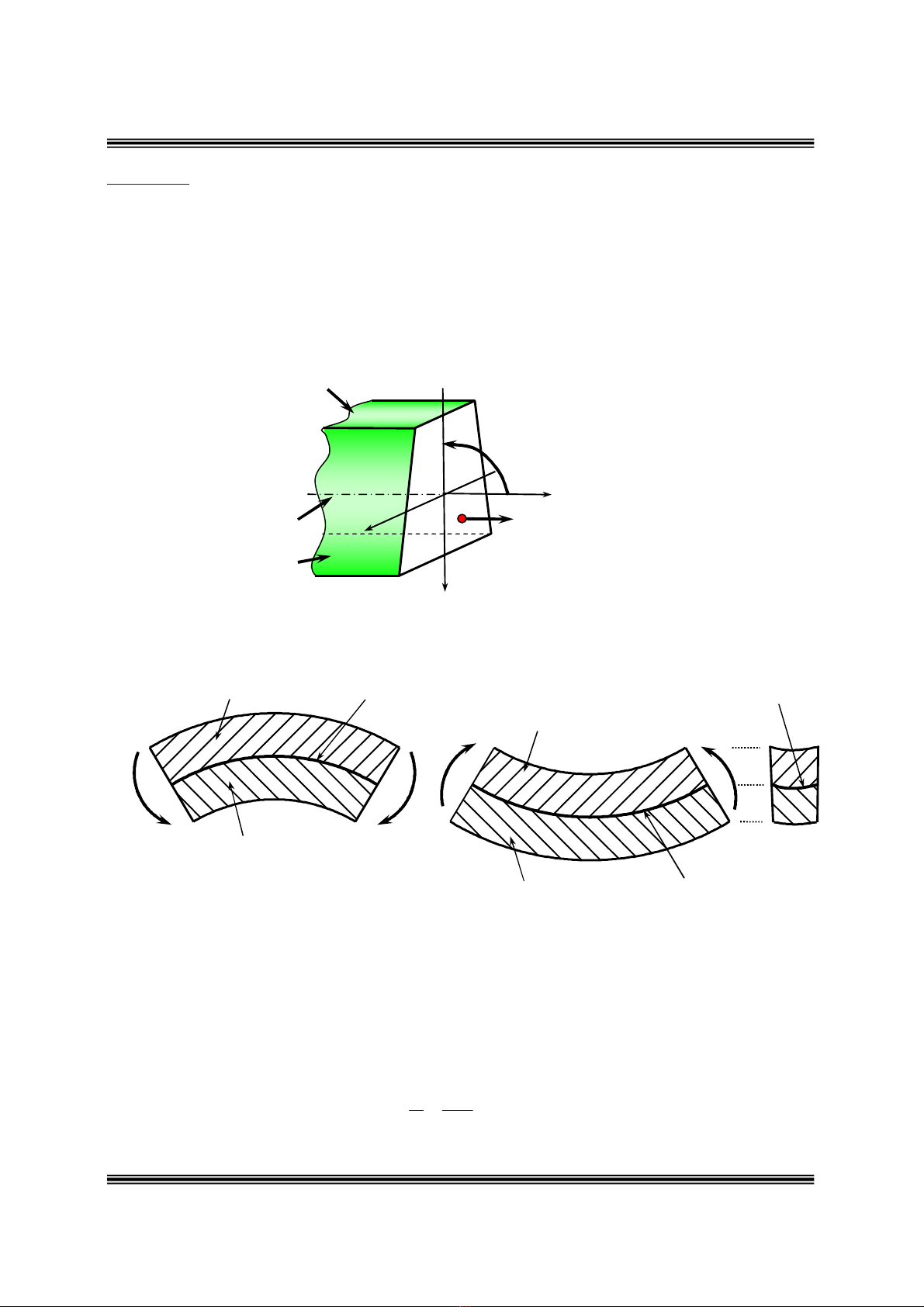
Trong thanh chòu uoán toàn taïi moät lôùp vaät lieäu khoâng chòu keùo vaø khoâng chòu neùn
ñöôïc goïi laø lôùp trung hoøa. Giao tuyeán cuûa lôùp trung hoøa vôùi maët caét ngang ñöôïc goïi laø
ñöôøng trung hoøa.
Ñöôøng trung hoøa chia maët caét laøm hai phaàn, phaàn chòu keùo, phaàn chòu neùn. Nhöõng
ñieåm naèm treân ñöôøng trung hoøa khoâng chòu keùo vaø khoâng chòu neùn neân coù öùng suaát
phaùp baèng khoâng.
Ñònh luaät Hooke:
.
z z
E
Ñoä cong cuûa ñöôøng ñaøn hoài: 1
x
x
M
EJ
(
laø baùn kính cong cuûa ñöôøng trung hoøa)
M
M
M
M
Phía vaät lieäu bò co laïi
Phía vaät lieäu bò giaõn ra Lôùp trung hoøa
Phía vaät lieäu bò
giaõn ra
Phía vaät lieäu bò co laïi
Lôùp trung hoøa
Ñöôøng trung hoøa
Hình
6.2
z
x
y
x
M
1
P
2
P
N
P
Z
A
Hình
6.1
Uoán phaúng thanh thaúng Khoa Xaây Döïng & Cô Hoïc ÖÙng Duïng
Baøi taäp söùc beàn vaät lieäu trang 2 05/2013
Vò trí truïc trung hoøa:
. . . . . 0 0
z z z x x
F F F F
y E E
N dF E dF E dF y dF S S
Ñöôøng trung hoøa
truøng vôùi truïc trung taâm cuûa maët caét ngang.
Phöông trình ñöôøng ñaøn hoài: ''
x
x
M
y
EJ
Quan heä giöõa moâmen uoán vaø öùng suaát phaùp:
2
. . . . .
x z z x
F F F F
y E E
M ydF E ydF E ydF y dF J
Öùng suaát phaùp doïc truïc do moâmen uoán
x
M
sinh ra: x
z
x
M
y
J
x
M
: moâmen uoán taïi maët caét coù ñieåm tính öùng suaát.
x
J
: moâmen quaùn tính chính trung taâm cuûa maët caét ngang coù ñieåm tính öùng suaát.
y
: khoaûng caùch töø ñieåm tính öùng suaát ñeán ñöôøng trung hoøa.
Öùng suaát phaùp phaân boá ñeàu theo beà roäng maët caét ngang vaø phaân boá tuyeán tính theo
chieàu cao tieát dieän: öùng suaát baèng khoâng ôû nhöõng ñieåm naèm treân ñöôøng trung hoøa vaø
lôùn nhaát taïi nhöõng ñieåm naèm xa nhaát so vôùi truïc trung hoøa.
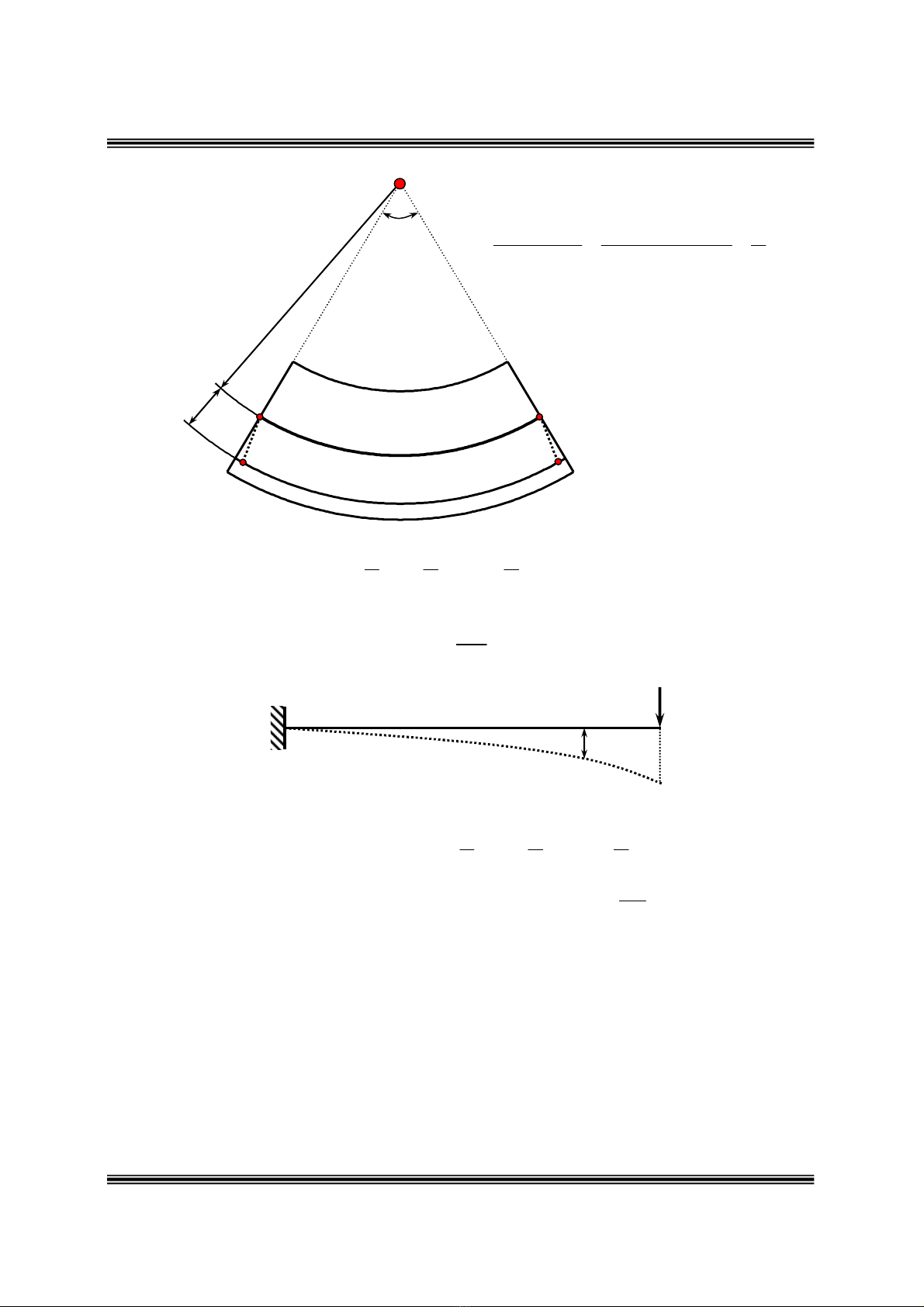
y
P
A
B
'
B
Hình
6.4
O
y
1
O
2
O
1
A
2
A
1
I
2
I
d
1 2 1 2
1 2
z
y d d
A A O O y
O O d
Hình
6.3
Uoán phaúng thanh thaúng Khoa Xaây Döïng & Cô Hoïc ÖÙng Duïng
Baøi taäp söùc beàn vaät lieäu trang 3 05/2013
Öùng suaát keùo lôùn nhaát treân maët caét ngang:
max max
k
x
x
M
y
J
Öùng suaát neùn lôùn nhaát treân maët caét ngang:
min max
n
x
x
M
y
J
Neáu maët caét ñoái xöùng: max min
max
;
x x
x
x
M J
W
W y
Neáu maët caét khoâng ñoái xöùng:
max min
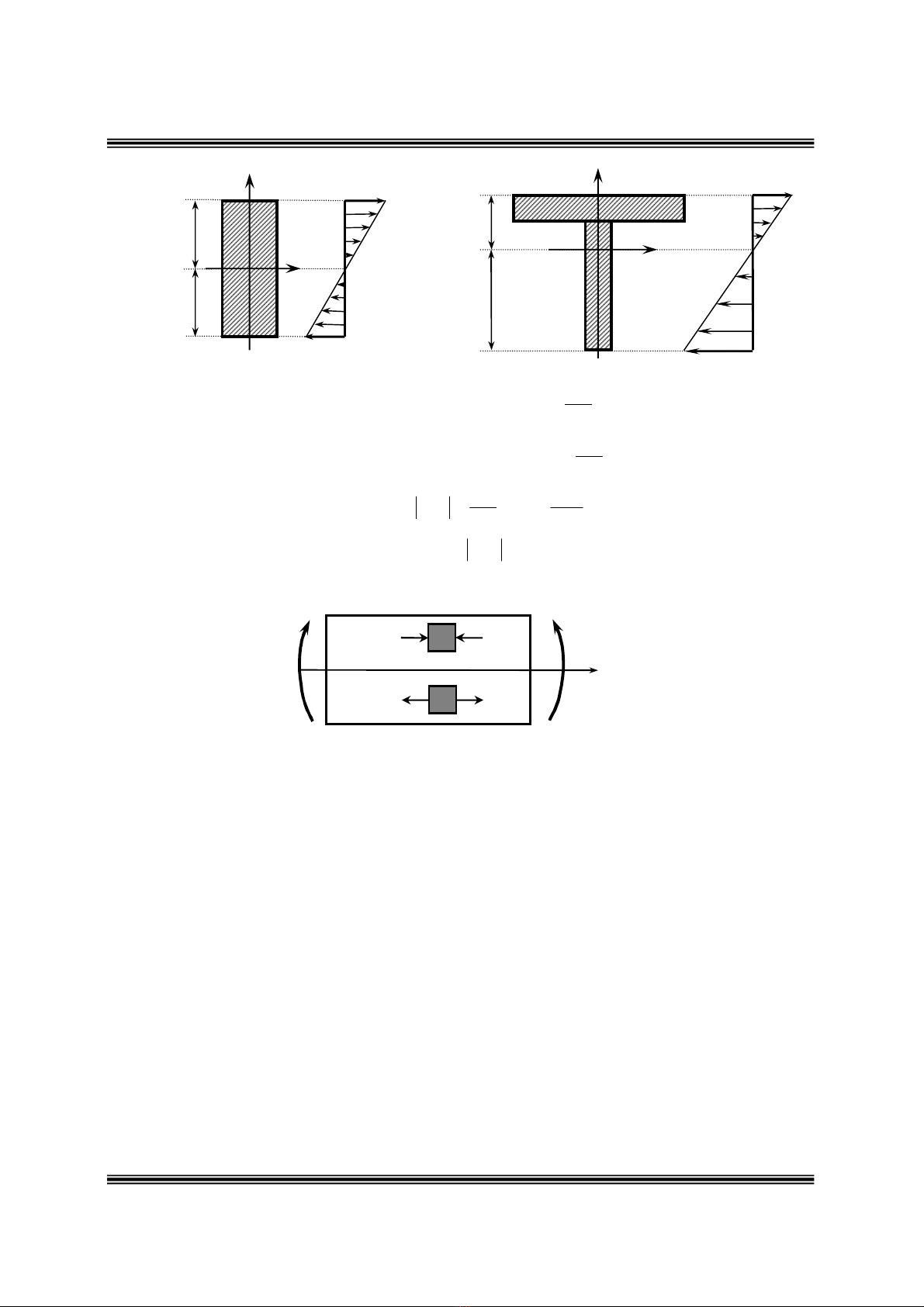
Öùng suaát treân phaân toá thuoäc daàm chòu uoán thuaàn tuùy
z
z
z
z
z
M
M
Hình
6.6
max
min
max
k
y
max
n
y
max
min
max
k
y
max
n
y
x
x
y
y
C
Hình
6.5
Uoán phaúng thanh thaúng Khoa Xaây Döïng & Cô Hoïc ÖÙng Duïng
Baøi taäp söùc beàn vaät lieäu trang 4 05/2013
Theá naêng bieán daïng ñaøn hoài: 2
2 .
x
x
L
M
U dz
E J
Ñieàu kieän beàn:
o Vaät lieäu deûo:
max
max max max max
max ; max( , )
xk n
z
x
My y y y
J
;
ch
n
o Vaät lieäu doøn:
max max
min max
;
;
k
x k
b
k k
x
n
xn
b
n n
x
My
J n
My
J n
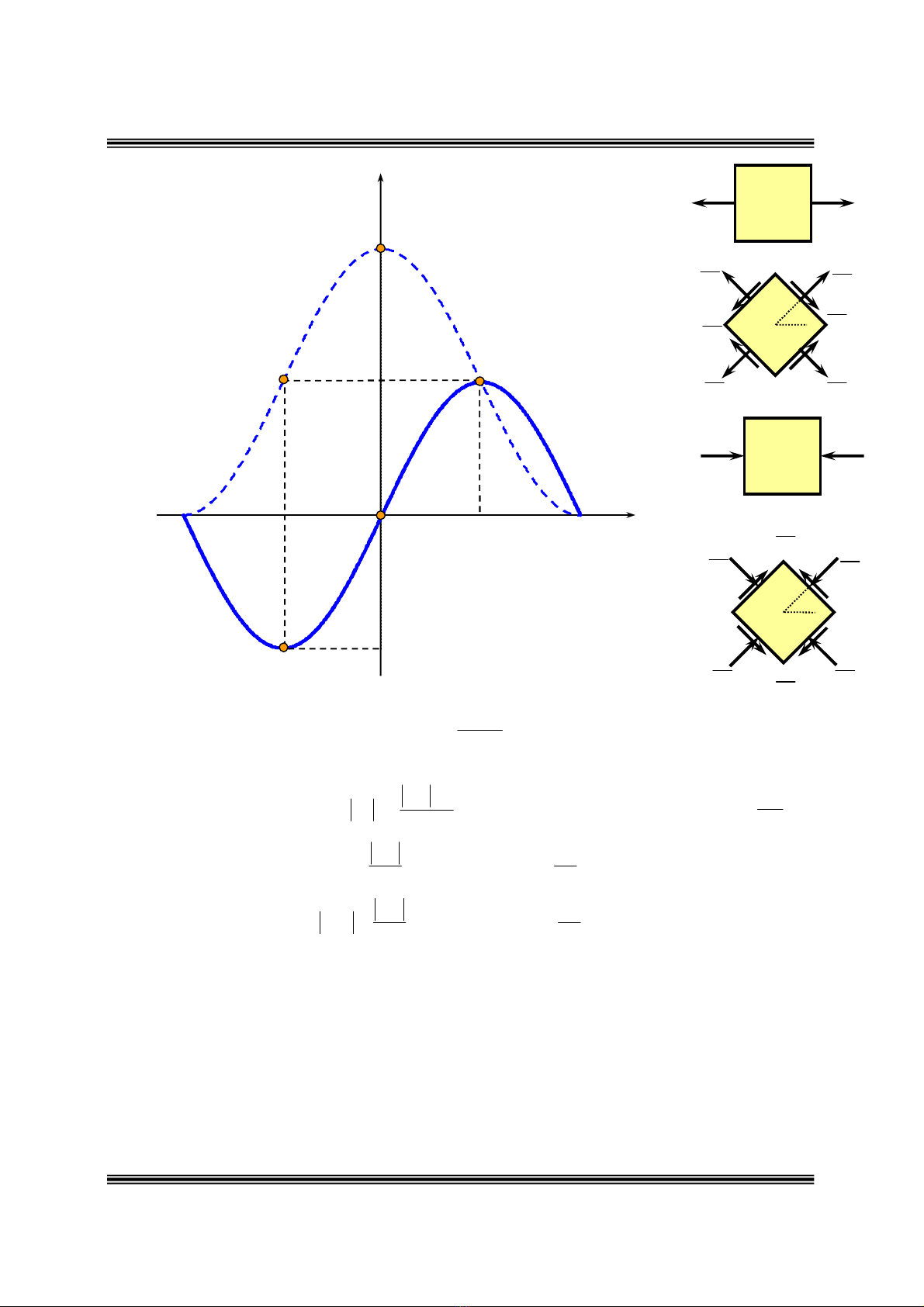
1.2 Thanh chòu uoán ngang phaúng
u
uv
0
90
0
90
0
45
0
45
x
0,5
x
0,5
x
0
u
uv
x
x
2
x
2
x
2
x
2
x
2
x
2
x
0
45
x
x
2
x
2
x
2
x
2
x
2
x
2
x
0
45
Uoán phaúng thanh thaúng Khoa Xaây Döïng & Cô Hoïc ÖÙng Duïng
Baøi taäp söùc beàn vaät lieäu trang 5 05/2013
Toàn taïi hai thaønh phaàn noäi löïc khaùc khoâng treân maët caét ngang, löïc caét
y
Q
vaø
moâmen uoán
x
M
.
Öùng suaát phaùp doïc truïc do
x
M
sinh ra: x
z
x
M
y
J
(nhö thanh chòu uoán thuaàn tuyù)
Öùng suaát tieáp treân maët caét ngang do
y
Q
sinh ra:
.
.
c
y x
zy
c
x
Q S
J b
y
Q
: löïc caét taïi maët caét coù ñieåm tính öùng suaát.
c
x
S
: moâmen tónh cuûa dieän tích bò caét ñoái vôùi truïc trung hoøa.
x
J
: moâmen quaùn tính chính trung taâm cuûa maët caét ngang.
c
b
: beà roäng maët caét taïi ñieåm tính öùng suaát.
Öùng suaát tieáp lôùn nhaát taïi nhöõng ñieåm naèm treân ñöôøng trung hoøa vaø ñöôïc tính:
/ 2
/ 2
max
.;
.
F
y x F
x
c
x
Q S
S
J b
: moâmen tónh cuûa moät nöõa dieän tích maët caét ngang so vôùi
truïc trung hoøa.
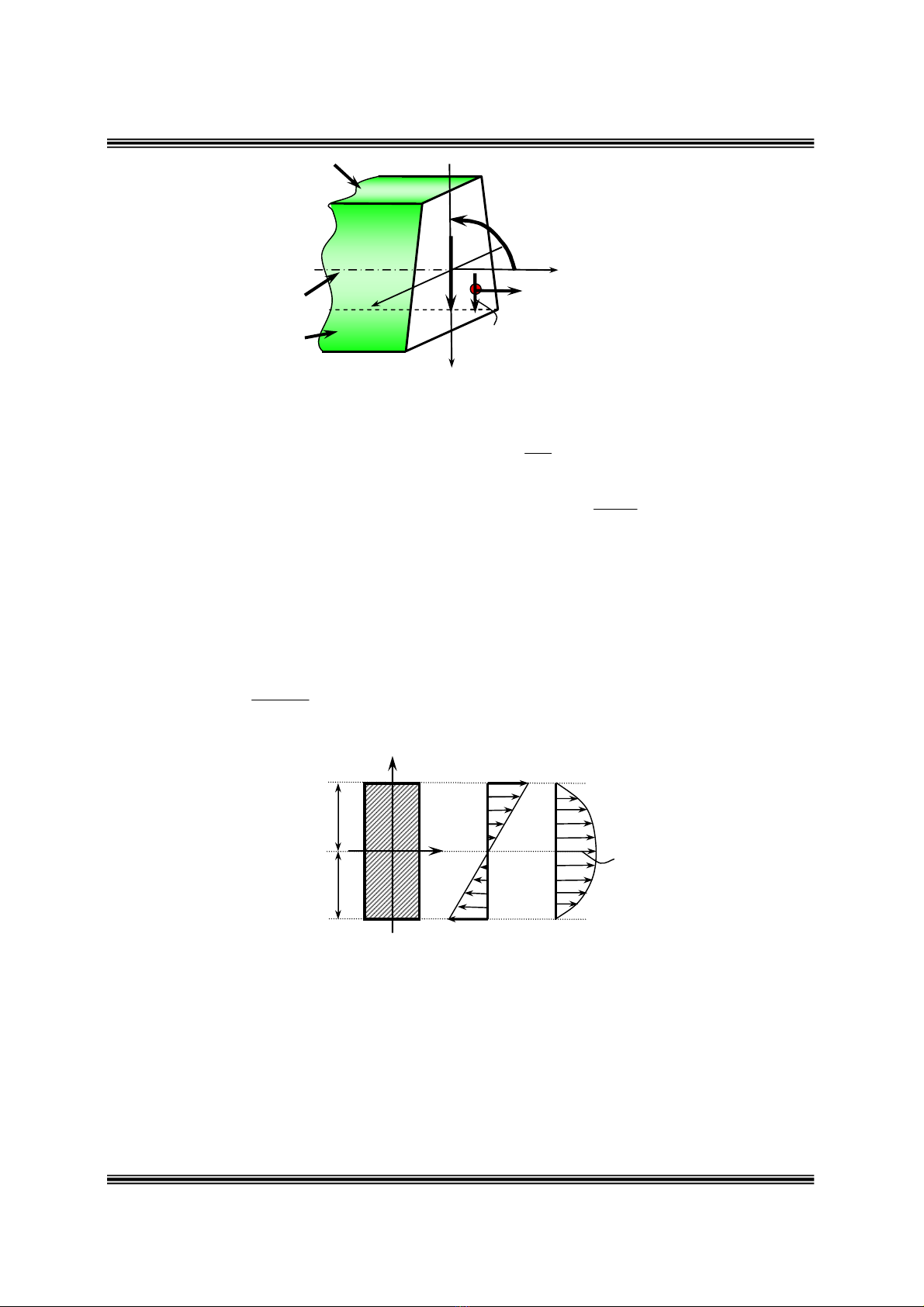
Öùng suaát treân phaân toá thuoäc daàm chòu uoán ngang phaúng
max
min
max
k
y
max
n
y
x
y
max
Hình
6.8
z
x
y
x
M
1
P
2
P
N
P
Z
A
y
Q
zy
Hình
6.7


























