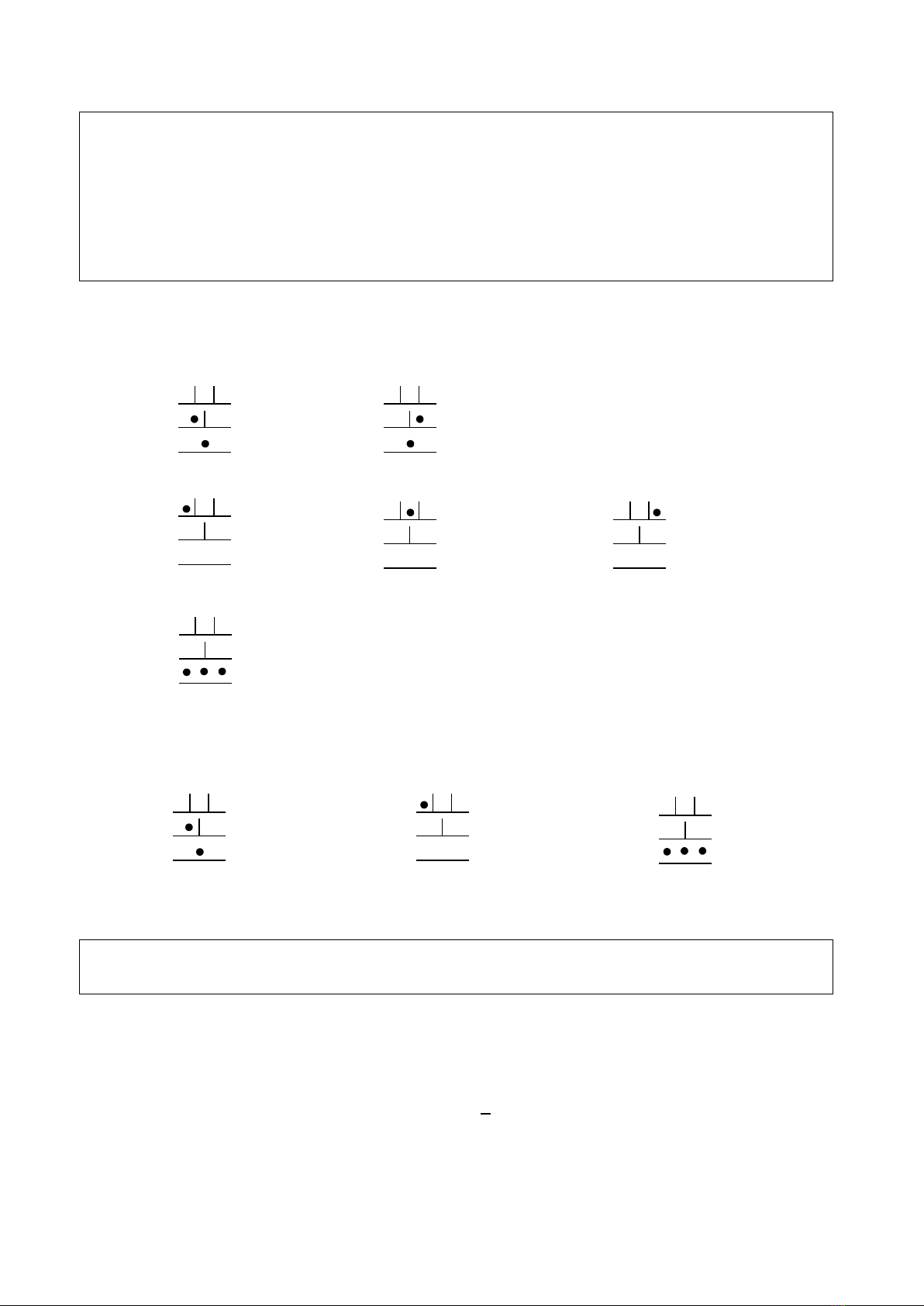
Cho hệ ba mức năng lượng =, =2, =3, có các bậc suy biến lần lượt là =1,
=2, =3. Những hạt không phân biệt được và được phân bố trên ba mức năng lượng này.
Hệ có năng lượng toàn phần là =3, và có số hạt không xác định. Gọi trạng thái vĩ mô là trạng
thái được đặc trưng bởi năng lượng =3, và số hạt trên mỗi mức năng lượng là như nhau.
Hãy vẽ sơ đồ phân bố các hạt trên các mức năng lượng và đếm số trạng thái vĩ mô cũng như số
trạng thái vi mô khả dĩ tương ứng với số trạng thái vĩ mô trên.
Vi mô: Ω=6
Vĩ mô: Ω=3
Một hệ gồm hai dao động tử điều hòa lượng tử độc lập, phân biệt được có tần số lần lượt là và
3. Tìm số trạng thái vi mô khả dĩ của hệ ứng với trạng thái vĩ mô có năng lượng 10.
Năng lượng dao động tử điều hòa ứng với tần số và 3 là:
=+12
=
=2
=3
=
=2
=3
=
=2
=3
=
=2
=3
=
=2
=3
=
=2
=3
=
=2
=3
=
=2
=3
=
=2
=3

=+123
Năng lượng toàn phần =10:
=+=+12++123=10
⇒+3=8
⇒=8
=0 ∨ =5
=1 ∨ =2
=2
⇒Ω=3
Xét một tinh thể rắn gồm nút mạng. Mỗi nút mạng có thể xem gần đúng gồm 3 dao động tử điều
hòa lượng tử một chiều độc lập phân biệt được, dao động với cùng tần số góc . Năng lượng tổng
cộng của tinh thể là
=ℏ
+32ℏ=
Trong đó, là số lượng tử của dao động tử điều hòa thứ . Số lượng tử của mạng tinh thể được
giữ ở =∑
.
a. Tính số trạng thái vi mô khả dĩ dứng với năng lượng và số lượng tử .
b. Hãy tìm hàm entropy theo nhiệt độ và số nút mạng .
a. Số trạng thái vi mô khả dĩ ứng với năng lượng và số lượng tử cũng giống như cách
sắp xếp hạt vào 3 cái hộp. Ta biểu diễn 3 cái hộp từ 3+1 vạch thẳng đứng, còn
các hạt biểu diễn bằng các ngôi sao (*), chẳng hạn như:
│**│*│***│****││*│
Như vậy, ở ngoài cùng luôn là 2 vạch thẳng đứng, bên trong còn lại 3−1 vạch và hạt.
Ta có số cách sắp xếp khác nhau bằng số cách chọn phần tử trong 3−1+ phần tử
bên trong:
=(3−1+)!
!(3−1)!
Số trạng thái vi mô khả dĩ ứng với năng lượng và số lượng tử là:
Ω=(3−1+)!
!(3−1)!
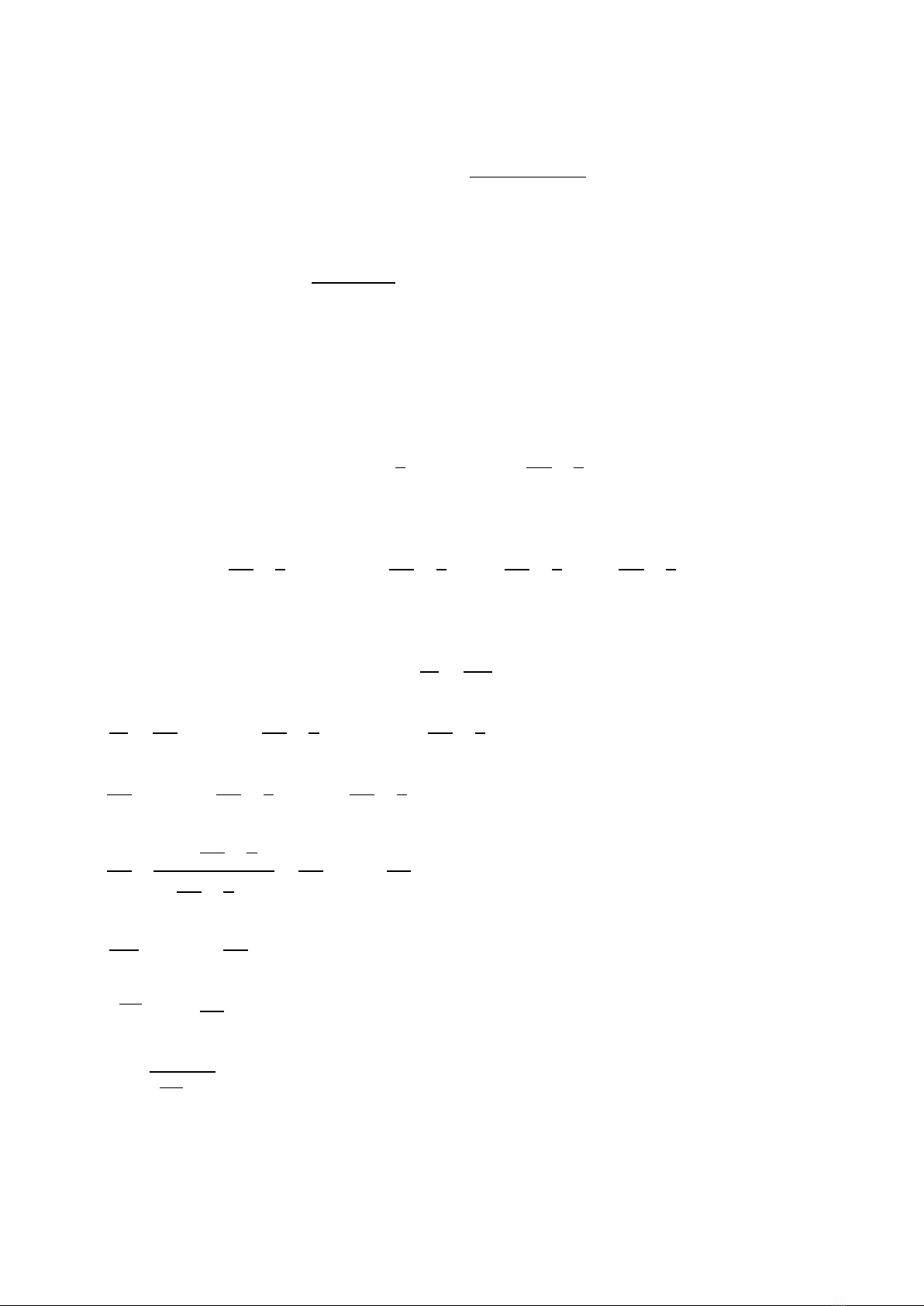
Entropy vi chính tắc của hệ có dạng:
∗=lnΩ=ln(3−1+)!
!(3−1)!
Vì ≫1, áp dụng công thức Stirling, suy ra:
∗=ln(3+)!
!(3)!=[ln(3+)!−ln!−ln3!]
=[(3+)ln(3+)−(3+)−ln+−3ln3+3]
=[(3+)ln(3+)−ln−3ln3]
Năng lượng tổng cộng của hệ:
=+32ℏ⇒=
ℏ−32
Thay vào ∗, ta được:
∗=3+
ℏ−32ln3+
ℏ−32−
ℏ−32ln
ℏ−32−3ln3
Gọi ∗ là nhiệt độ vi chính tắc, ta có hệ thức:
1
∗=∗
⇒1
∗=
ℏln3+
ℏ−32+1−ln
ℏ−32−1
=
ℏln3+
ℏ−32−ln
ℏ−32
=
ℏln3+
ℏ−32
ℏ−32=
ℏln1+3
⇒ℏ
∗=ln1+3
⇒ℏ
∗=1+3
⇒= 3
ℏ
∗−1

Thay vào ∗, ta được đáp số:
∗(∗,)=3+ 3
ℏ
∗−1ln3+ 3
ℏ
∗−1− 3
ℏ
∗−1ln 3
ℏ
∗−1−3ln3
Một hạt có spin ½ được đặt vào trong từ trường
sẽ có thể hướng dọc theo từ trường hoặc ngược
lại. Năng lượng tương ứng là ℋ=
=+, ↓
−, ↑
a. Một hệ có ba hạt đặt vào trong từ trường
. Các hạt là phân biệt được. Các trạng thái vĩ
mô có cùng tổng năng lượng được xem là cùng một trạng thái vĩ mô. Hãy tính số trạng
thái vi mô và số trạng thái vĩ mô tương ứng.
b. Xét hệ hạt phân biệt được. Hãy tính số trạng thái vi mô tương ứng với trạng thái vĩ mô
được xác định bởi năng lượng .
a. Số trạng thái vi mô: Ω=8
Số trạng thái vĩ mô: Ω=4
1 hạt mang 2 giá trị spin (↓,↑), do đó 3 hạt có Ω=2=8 trạng thái vi mô.
3 hạt sẽ có 4 trạng thái vĩ mô là:
+ 3 hạt có spin cùng chiều
(−3)
+ 2 hạt có spin cùng chiều
và 1 hạt có spin ngược chiều
(−)
+ 1 hạt có spin cùng chiều
và 2 hạt có spin ngược chiều
(+)
+ 3 hạt có spin ngược chiều
(+3)
↑↑↑ ⟶−3
↑↑↓ ↑↓↑ ↓↑↑ ⟶−
↓↓↑ ↓↑↓ ↑↓↓ ⟶+
↓↓↓ ⟶+3
b. Ta có: −≤≤+
Năng lượng: = với ∈ℤ

Gọi là số hạt có spin hướng lên ↑ (cùng chiều
)
số hạt có spin hướng xuống ↓ (ngược chiều
) là
Ta có: =− và =+
⇒=−
2=−
2
Số trạng thái vi mô tương ứng với trạng thái vĩ mô được xác định bởi năng lượng E cũng chính là
cách sắp xếp hạt trong vị trí.
=!
−
2!+
2!
Thành phần Hamiltonian theo spin của một hệ ion được cho bởi:
ℋ=
Trong đó, có thể có các giá trị 0, ±1. Thành phần Hamiltonian này mô tả hiệu ứng tĩnh điện lên
các ion spin 1.
a. Hãy chứng tỏ rằng, số trạng thái vi mô khả dĩ ứng với trạng thái vĩ mô có năng lượng là
(,)=!
−
!
−!!
b. Với ,→∞ và /= vẫn không đổi, chứng tỏ rằng:
1
=
2−1−
1−
−
Biểu thức này là entropy trung bình trên mỗi hạt trong hệ đơn vị hằng số Boltzmann .
a. Số trạng thái vi mô ứng với bộ 3 số (,,) với =+− là:
Ω(,,)=
=!
!(−)!(−)!
!(−−)!=!
!!!


























