Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com
https://www.facebook.com/trithuc.viet.37 1
BÀI TOÁN KHOẢNG CÁCH
A. CƠ SỞ LÍ THUYẾT
1. Khoảng cách từ một điểm đến một đường thẳng
Cho điểm O và đường thẳng . Gọi H là hình chiếu của O trên . Khi đó khoảng cách giữa hai
điểm O và H được gọi là khoảng cách từ điểm O đến đường thẳng . Kí hiệu
( , )
d O
* Nhận xét
-
, ( , )
M OM d O
- Để tính khoảng cách từ điểm O đến đường thẳng ta có thể
+ Xác định hình chiếu H của O trên và tính OH
+ Áp dụng công thức
2. Khoảng cách từ một điểm đến một mặt phẳng
Cho điểm O và mặt phẳng (). Gọi H là hình chiếu của O trên (). Khi đó khoảng cách giữa hai
điểm O và H được gọi là khoảng cách từ điểm O đến mặt phẳng (). Kí hiệu
( ,( ))
d O
* Nhận xét
-
( ), ( ,( ))
M OM d O
- Để tính khoảng cách từ điểm O đến mặt phẳng () ta có thể sử dụng một trong các cách sau:
Cách 1. Tính trực tiếp. Xác định hình chiếu H của O trên () và tính OH
* Phương pháp chung.
- Dựng mặt phẳng (P) chứa O và vuông góc với ()
- Tìm giao tuyến của (P) và ()
- Kẻ OH (
H
). Khi đó ( ,( ))
d O OH
. Đặc biệt:
+ Trong hình chóp đều, thì chân đường cao hạ từ đỉnh trùng với tâm đáy
+ Hình chóp có một mặt bên vuông góc với đáy thì chân đường vuông góc hạ từ đỉnh sẽ thuộc
giao tuyến của mặt bên đó với đáy
+ Hình chóp có 2 mặt bên vuông góc với đáy thì đường cao chính là giao tuyến của hai mặt bên
này
+ Hình chóp có các cạnh bên bằng nhau (hoặc tạo với đáy những góc bằng nhau) thì chân đường
cao là tâm đường tròn ngoại tiếp đáy
+ Hình chóp có các mặt bên tạo với đáy những góc bằng nhau thì chân đường cao là tâm đường
tròn nội tiếp đáy
Cách 2. Sử dụng công thức thể tích
Thể tích của khối chóp
1 3
.
3
V
V S h h
S
. Theo cách này, để tính khoảng cách từ đỉnh của hình
chóp đến mặt đáy, ta đi tính V và S
Cách 3. Sử dụng phép trượt đỉnh
Ý tưởng của phương pháp này là: bằng cách trượt đỉnh O trên một đường thẳng đến một vị trí
thuận lợi
'
O
, ta quy việc tính
( ,( ))
d O
về việc tính
( ',( ))
d O
. Ta thường sử dụng những kết quả sau:
Kết quả 1. Nếu đường thẳng song song với mặt phẳng () và M, N thì
( ;( )) ( ;( ))
d M d N
Kết quả 2. Nếu đường thẳng cắt mặt phẳng () tại điểm I và M, N (M, N không trùng với I) thì
( ;( ))
( ;( ))
d M MI
d N NI
Đặc biệt, nếu M là trung điểm của NI thì 1
( ;( )) ( ;( ))
2
d M d N
nếu I là trung điểm của MN thì
( ;( )) ( ;( ))
d M d N
Cách 4. Sử dụng tính chất của tứ diện vuông
Cơ sở của phương pháp này là tính chất sau: Giả sử OABC là tứ diện vuông tại O
(, ,
OA OB OB OC OC OA
) và H là hình chiếu của O trên mặt phẳng (ABC). Khi đó đường cao OH
được tính bằng công thức
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com
https://www.facebook.com/trithuc.viet.37 2
2 2 2 2
1 1 1 1
OH OA OB OC
Cách 5. Sử dụng phương pháp tọa độ
Cơ sở của phương pháp này là ta cần chọn hệ tọa độ thích hợp sau đó sử dụng các công thức sau:
0 0 0
2 2 2
( ;( ))
Ax By Cz D
d M
ABC
với
0 0 0
( ; ; )
M x y z
,
( ) : 0
Ax By Cz D
( , )
MA u
d M
u
với là đường thẳng đi qua A và có vectơ chỉ phương
u
'. '
( , ')
'
u u AA
d
u u
với
'
là đường thẳng đi qua
'
A
và có vtcp
'
u
Cách 6. Sử dụng phương pháp vectơ
3. Khoảng cách từ một đường thẳng đến một mặt phẳng song song với nó
Cho điểm đường thẳng song song với mặt phẳng (). Khoảng cách giữa đường thẳng và mặt
phẳng () là khoảng cách từ một điểm bất kì của đến mặt phẳng (). Kí hiệu
( ,( ))
d
* Nhận xét
-
, ( ), ( ,( ))
M N MN d
- Việc tính khoảng cách từ đường thẳng đến mặt phẳng () được quy về việc tính khoảng cách từ
một điểm đến một mặt phẳng.
4. Khoảng cách giữa hai mặt phẳng song song
Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm bất kì của mặt phẳng này
đến mặt phẳng kia. Kí hiệu
(( );( ))
d
* Nhận xét
-
( ), ( ), (( );( ))
M N MN d
- Việc tính khoảng cách giữa hai mặt phẳng song song được quy về việc tính khoảng cách từ một
điểm đến một mặt phẳng.
5. Khoảng cách giữa hai đường thẳng chéo nhau
Cho hai đường thẳng chéo nhau a và b. Đường thẳng cắt cả a và b đồng thời vuông góc với cả a
và b được gọi là đường vuông góc chung của a và b. Đường vuông góc chung cắt a tại H và cắt b tại K
thì độ dài đoạn thẳng MN gọi là khoảng cách giữa hai đường thẳng chéo nhau a và b. Kí hiệu
( , )
d a b
.
* Nhận xét
-
, , ( , )
M a N b MN d a b
- Để tính khoảng cách hai đường thẳng chéo nhau a và b ta làm như sau:
+ Tìm H và K từ đó suy ra ( , )
d a b HK
+ Tìm một mặt phẳng (P) chứa a và song song với b. Khi đó
( , ) ( ,( ))
d a b d b P
+ Tìm cặp mặt phẳng song song (P), (Q) lần lượt chứa a và b. Khi đó
( , ) (( ),( ))
d a b d P Q
+ Sử dụng phương pháp tọa độ
* Đặc biệt
- Nếu
a b
thì ta tìm mặt phẳng (P) chứa a và vuông góc với b, tiếp theo ta tìm giao điểm I của (P)
với b. Trong mp(P), hạ đường cao IH. Khi đó ( , )
d a b IH
- Nếu tứ diện ABCD có AC = BD, AD = BC thì đoạn thẳng nối hai trung điểm của AB và CD là
đoạn vuông góc chung của AB và CD.
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com
https://www.facebook.com/trithuc.viet.37 3
B. CÁC VÍ DỤ MINH HOẠ
I) Phương pháp tính trực tiếp
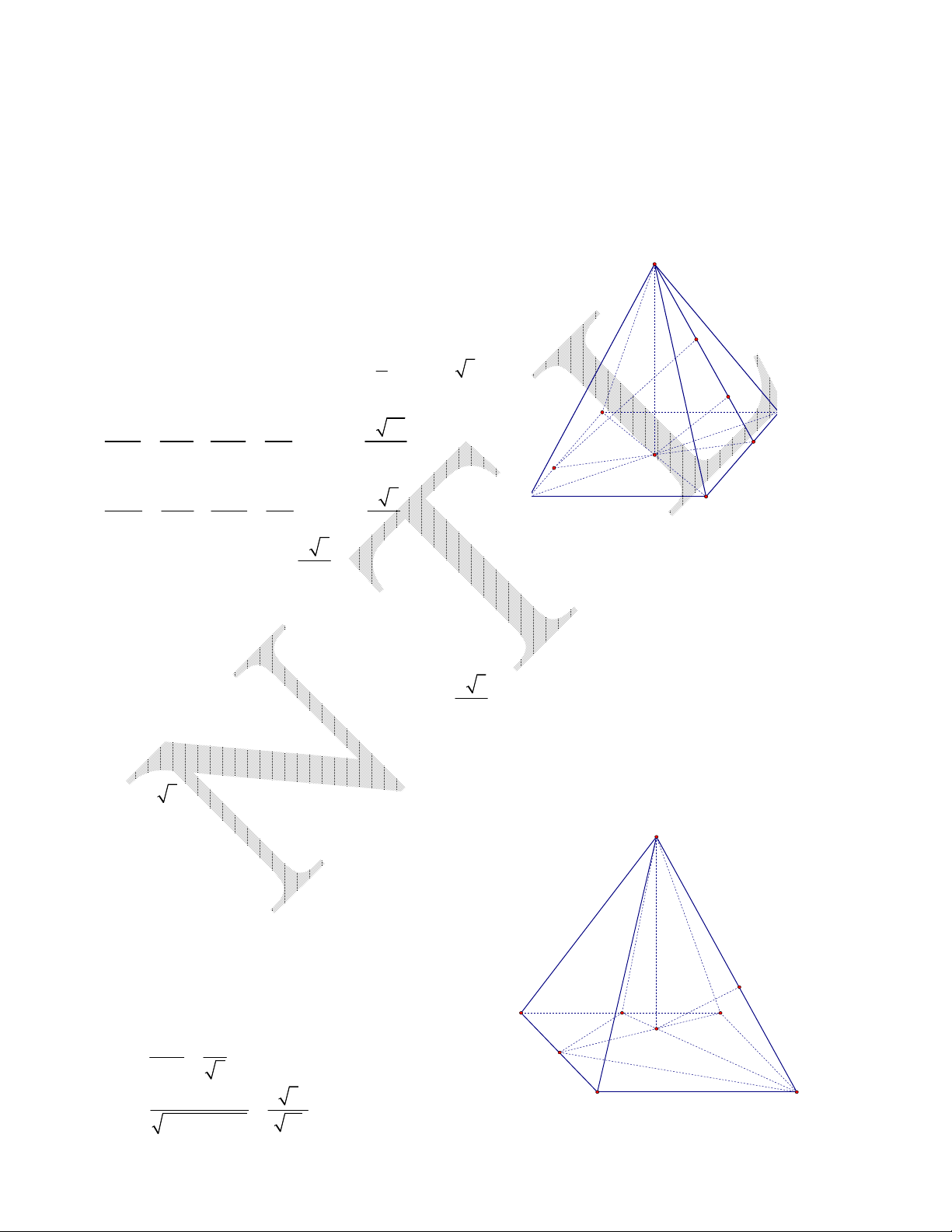
Ví dụ 1. Cho hình chóp SABCD có đáy ABCD là hình thoi tâm O, cạnh a, góc
0
60
BAD , có SO vuông
góc mặt phẳng (ABCD) và SO = a.
a) Tính khoảng cách từ O đến mặt phẳng (SBC).
b) Tính khoảng cách từ đường thẳng AD đến mặt phẳng (SBC).
Lời giải.
a) Hạ
OK BC BC SOK
Trong (SOK) kẻ
OH SK OH SBC
,
d O SBC OH
.
Ta có
ABD
đều
2
a
BD a BO ;
3
AC a
Trong tam giác vuông OBC có:
2 2 2 2
1 1 1 13 39
13
3
a
OK
OK OB OC a
Trong tam giác vuông SOK có:
2 2 2 2
1 1 1 16 3
4
3
a
OH
OH OS OK a
Vậy
3
,
4
a
d O SBC OH
b) Ta có
/ / / /
AD BC AD SBC
, ,
d AD SBC d E SBC
Kẻ
/ /
EF OH F SK
. Do
OH SBC EF SBC
3
, , 2
2
a
d AD SBC d E SBC EF OH
Ví dụ 2. (Đề thi Đại học khối A năm 2010).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi M và N lần lượt là trung điểm của các
cạnh AB và AD; H là giao điểm của CN với DM. Biết SH vuông góc với mặt phẳng (ABCD) và
3
SH a
. Tính khoảng cách giữa hai đường thẳng DM và SC theo a.
Lời giải.
Ta có:
MAD NCD ADM DCN
MD NC
Do
SH ABCD MD SH
MD SHC
Kẻ
HK SC K SC
Suy ra HK là đoạn vuông góc chung của DM và SC
nên
,
d DM SC HK
Ta có:
2
2
5
CD a
HC CN
2 2
2 3
19
SH HC a
HK
SH HC
M
N
H
K
D
C
B
A
S
K
F
E
D
C
B
A
S
H
O
D
B
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com
https://www.facebook.com/trithuc.viet.37 4
Vậy
2 3
,
19
a
d DM SC
II) Phương pháp sử dụng công thức tính thể tích.
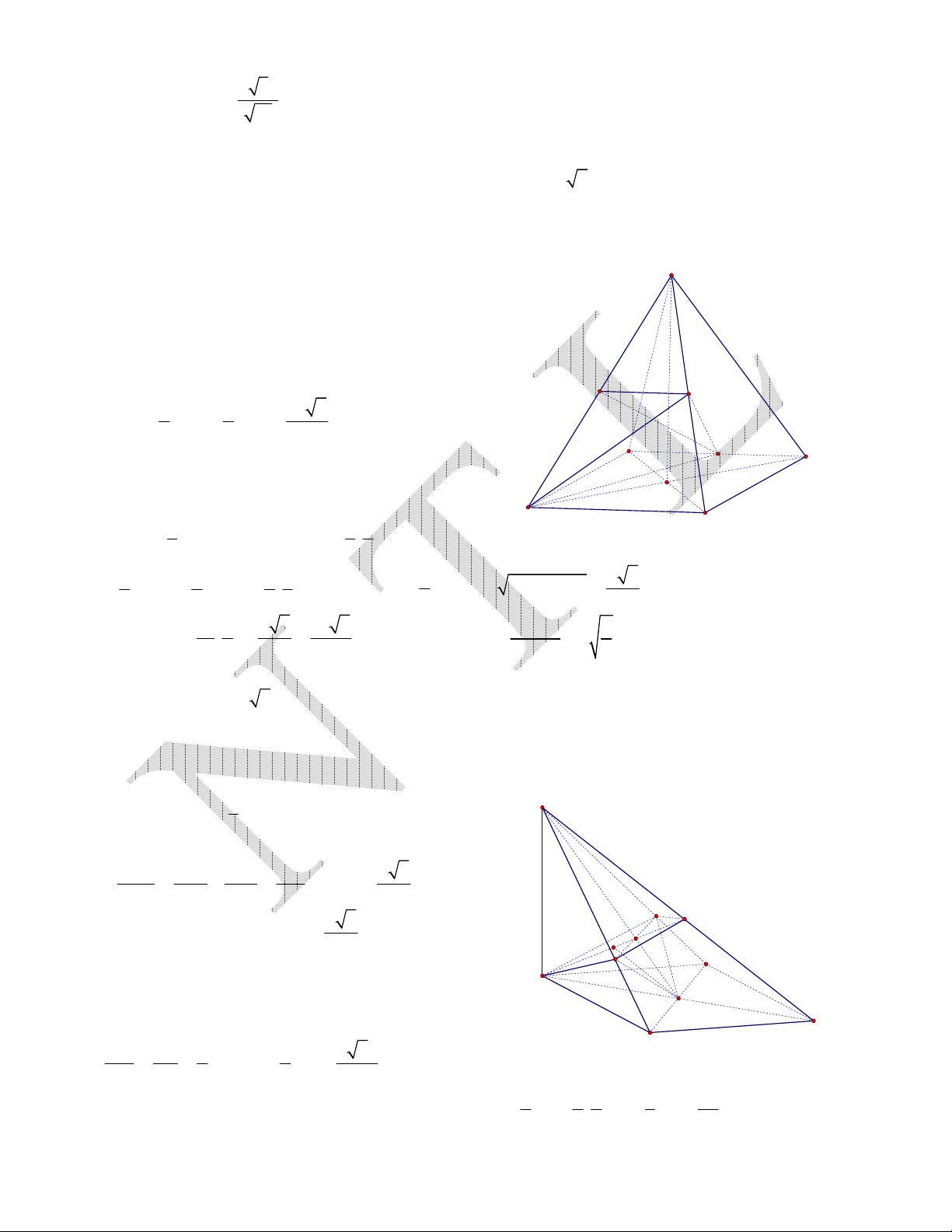
Ví dụ 3. Cho hình chóp tứ giác đều S.ABCD có AB = a, SA =
2
a
. Gọi M, N, P lần lượt là trung điểm
của các cạnh SA, SB, CD. Tính khoảng cách từ P đến mặt phẳng (AMN).
Phân tích. Theo giả thiết, việc tính thể tích các khối chóp S.ABCD hay S.ABC hay AMNP là dễ dàng.
Vậy ta có thể nghĩ đến việc quy việc tính khoảng cách
từ P đến mặt phẳng (AMN) về việc tính thể tích của
các khối chóp nói trên, khoảng cách từ P đến (AMN)
có thể thay bằng khoảng cách từ C đến (SAB).
Lời giải.
Gọi O là tâm của hình vuông ABCD, khi đó SO
(ABCD).
M, N lần lượt là trung điểm của SA và SB nên
2
1 1 7
2 4 16
AMN ANS ABS
a
S S S
/ /( )
( ,( )) ( ,( ))
PC AMN
d P AMN d C AMN .
Vậy:
.
1 1 1
. ( ,( )) . . ( ,( ))
3 3 4
P AMN AMN ABS
V S d P AMN S d C AMN
. .
1 1 1 1
. .
4 4 4 3
C ABS S ABC ABC
V V S SO
. 2 2 2
1 6
,
2 2
ABC
a
S a SO SA AO .
Vậy
3
2
1 1 6 6
. .
12 2 2 48
AMNP
a a
V a
3
6
( ,( ))
7
PAMN
AMN
V
d P AMN a
S
Ví dụ 4. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, SA vuông góc với đáy hình chóp.
Cho AB = a, SA =
2
a
. Gọi H, K lần lượt là hình chiếu của A trên SB, SD. Tính khoảng cách từ điểm O
đến mặt phẳng (AHK).
Phân tích. Khối chóp AOHK và ASBD có chung đỉnh, đáy cùng nằm trên một mặt phẳng nên ta có thể
tính được thể tích khối chóp OAHK, hơn nữa tam giác AHK cân nên ta tính được diện tích của nó.
Lời giải.
Cách 1:
1. ;
3
OAHK AHK
V S d O AHK
Trong đó:
2 2 2 2
1 1 1 3 6
3
2
a
AH
AH AB AS a
;
6
3
a
SAD SAB AK AH
Ta có HK và BD đồng phẳng và cùng vuông góc với SC
nên HK // BD.
AI cắt SO tại G là trọng tâm của tam giác SAC, G thuộc
HK nên
2 2 2 2
3 3 3
HK SG a
HK BD
BD SO
. Tam giác AHK
cân tai A, G là trung điểm của HK nên AG HK và
2 2 1 1 2
. .2
3 3 2 3 3
a
AG AI SC a
P
N
M
O
B
D
C
A
S
O
C
A
D
B
S
H
K
J G
I
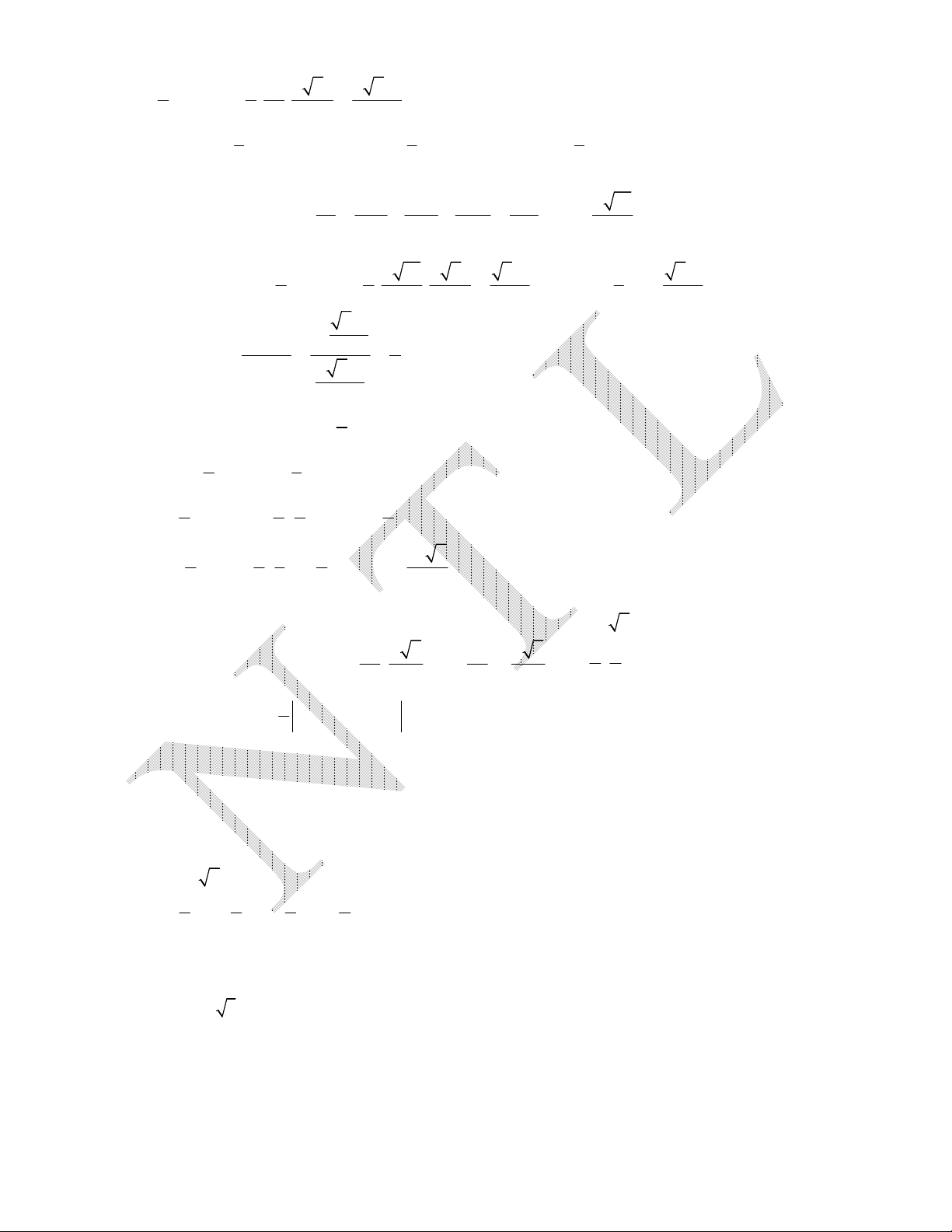
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com
https://www.facebook.com/trithuc.viet.37 5
2
1 1 2 2 2 2 2
. . .
2 2 3 3 9
AHK
a a a
S AG HK
1 1 1
; . ; . .
3 3 3
OAHK AOHK OHK OHK OHK
V V d A OHK S d A SBD S h S
Tứ diện ASBD vuông tại A nên:
2 2 2 2 2
1 1 1 1 5 10
5
2
a
h
h AS AB AD a
Tam giác OHK cân tại O nên có diện tích S bằng
2 3
1 1 10 2 2 5 1 2
. . .
2 2 6 3 9 3 27
OAHK
a a a a
S OG HK V Sh
3
2
2
3
327
;
2
2 2
9
OAHK
AHK
a
V
a
d O AHK Sa
Cách 2: Ta chứng minh 2
9
OAHK SABD
V V
Ta có: 2 1
;
3 3
HK BD OG SO
1 1 2 2
2 2 9 9
OHK SBD
S HK OG BD SO S
3
2 2 1 1 2
9 9 3 2 27
AOHK SABD
a
V V SA AB AD
Cách 3: Giải bằng phương pháp tọa độ như sau:
Chọn hệ tọa độ Oxyz sao cho O A, B(a ; 0 ; 0), D(0 ; a ; 0), S(0 ; 0 ;
2
a
).
Tính SH, SK suy ra tọa độ của H
2 2
0; ;
3 3
a a , K
2 2
;0;
3 3
a a , O
; ;0
2 2
a a
Áp dụng công thức 1, .
6
 
V AH AK AO
Cách 4: SC
(AHK) nên chân đường vuông góc hạ từ O xuông (AHK) có thể xác định được theo phương
SC.
* AH SB, AH BC (do BC (SAB)) AH SC
Tương tự AK SC. Vậy SC (AHK)
* Giả sử (AHK) cắt SC tại I, gọi J là trung điểm của AI, khi đó OJ // SC
OJ (AHK).
SA = AC =
2
a
SAC cân tại A I là trung điểm của SC.
Vậy 1 1 1 .2
2 4 4 2
a
OJ IC SC a
III) Phương pháp trượt
Ví dụ 5. (Đề thi Đại học khối B năm 2011). Cho lăng trụ ABCDA1B1C1D1 có đáy ABCD là hình chữ nhật
, 3
AB a AD a
. Hình chiếu vuông góc của điểm A1 trên mặt phẳng (ABCD) trùng với giao điểm của
AC và BD, góc giữa hai mặt phẳng (ADD1A1) và (ABCD) bằng 600. Tính thể tích của khối lăng trụ đã cho
và khoảng cách từ điểm B1 đến mặt phẳng (A1BD) theo a.
Phân tích. Do B1C // (A1BD) nên ta trượt đỉnh B1 về vị trí thuận lợi C và quy việc tính
1 1
;
d B A BD
thành tính
1
;
d C A BD