CÁC BÀI TOÁN HÌNH KHÔNG GIAN CHO THI ĐẠI HỌC
1 - Khối chóp
Bài 1.1. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a,tam giác S AB đều và
S AD =900.Jlà trung điểm SD. Tính theo athể tích khối tứ diện ACD J và khoảng cách từ D
đến mặt phẳng (ACJ).
Giải:
A
B
D
C
I
S
J
+(AD ⊥S A
AD ⊥AB ⇒AD ⊥(S AB)
+ Gọi Ilà trung điểm AB thì AD ⊥SI (1). Mà ∆S AB đều nên SI ⊥AB (2)
Từ (1) và (2) suy ra S I ⊥(ABCD).Do đó d(J,(ACD)) =1
2d(S,(ABCD)) =1
2SI =ap3
4
Từ đó suy ra VACD J =1
3.1
2.a2.ap3
4=a3p3
24 .
∆BCI vuông tại Bnên C I2=CB2+BI2=5a2
4
∆SIC vuông tại Inên SC2=SI2+IC2=2a2
Tương tự SD2=SC2=2a2
∆SCD có CJ là đường trung tuyến nên CJ2=SC2+CD2
2−SD4
4=a2
Xét ∆J AC có J A =a
p2;AC =ap2; CJ =anên tính được cosA =3
4
Từ đó sin
J AC =p7
4nên dt(J AC)=1
2.a
p2.p7
4=a2p7
8
Vậy d(D,(J AC)) =
3.a3p3
24
a2p7
8
=ap21
7
Nhận xét: Có thể tính diện tích tam giác JAC bằng cách lấy hình chiếu của J trên mặt đáy (là
trung điểm H của DI). Trong mặt đáy, kẻ HK vuông góc với AC (hay HK song song với BD) với
K thuộc AC thì chỉ ra được JK vuông góc với AC và tính được JK là đường cao tam giác JAC.
Bài 1.2. Cho hình chóp S.ABCD có đáy ABCD là hình thoi ; hai đường chéo AC =2p3a,BD =
2avà cắt nhau tại O;hai mặt phẳng (S AC)và (SBD)cùng vuông góc với mặt phẳng (ABCD).
Biết khoảng cách từ điểm Ođến mặt phẳng (S AB)bằng ap3
4, tính thể tích khối chóp S.ABCD
theo a.
http://boxmath.vn/ 1
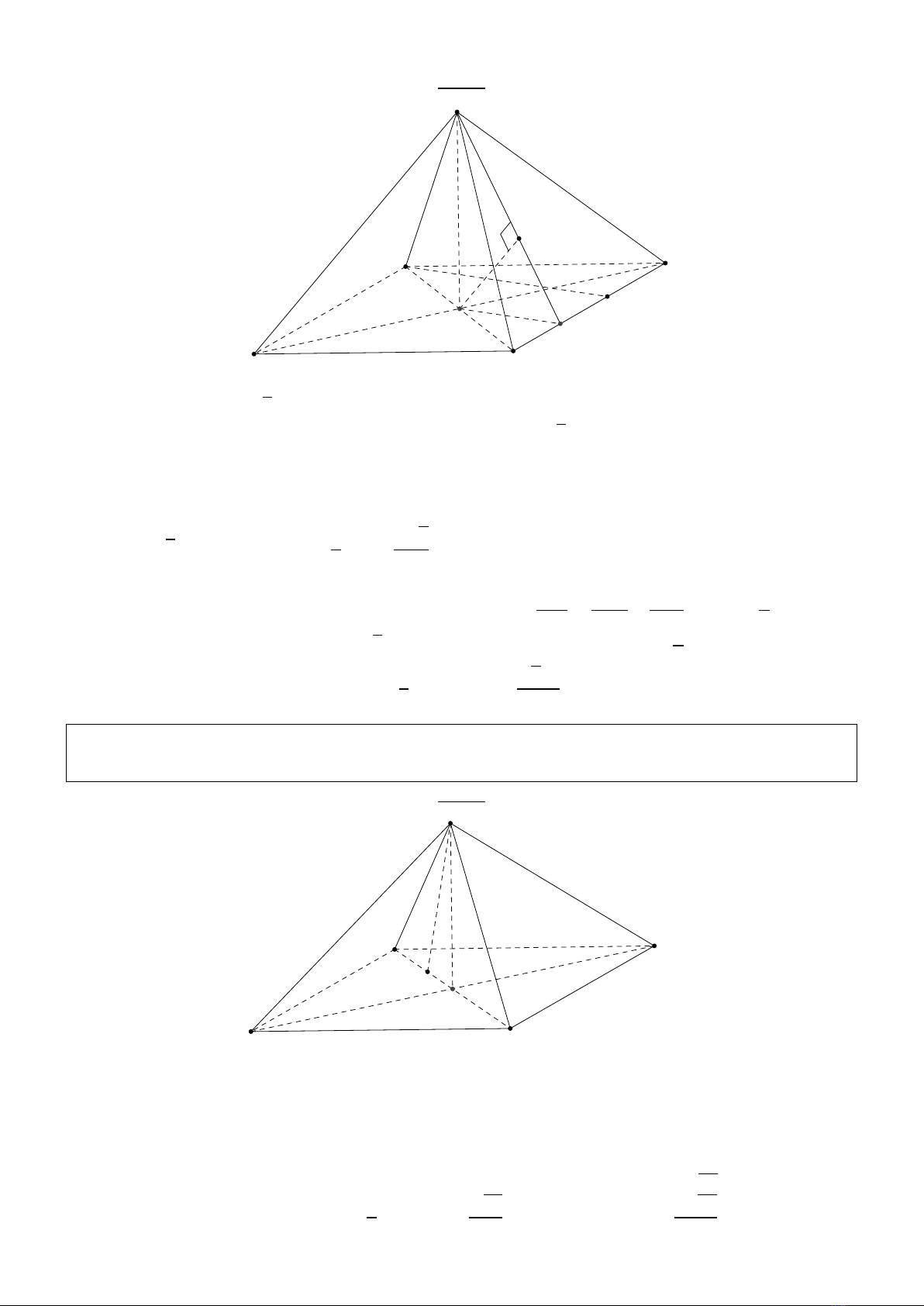
Giải:
DA
CB
O
S
H
K
I
Từ giả thiết AC =2ap3; BD =2avà AC,BD vuông góc với nhau tại trung điểm Ocủa mỗi
đường chéo. Ta có tam giác ABO vuông tại Ovà AO =ap3; BO =a,do đó
ABD =60ohay tam
giác ABD đều. Từ giả thiết hai mặt phẳng (S AC)và (SBD)cùng vuông góc với mặt phẳng
(ABCD)nên giao tuyến của chúng là SO ⊥(ABCD).
Do tam giác ABD đều nên với Hlà trung điểm của AB,Klà trung điểm của HB ta có DH ⊥AB
và DH =ap3; OK//DH và OK =1
2DH =ap3
2⇒OK ⊥AB ⇒AB ⊥(SOK)Gọi Ilà hình chiếu của
Olên SK ta có OI ⊥SK;AB ⊥OI ⇒OI ⊥(S AB),hay OI là khoảng cách từ Ođến mặt phẳng
(S AB).Tam giác SOK vuông tại O,OI là đường cao ⇒1
OI2=1
OK2+1
SO2⇒SO =a
2Diện tích
đáy SABCD =4S∆ABO =2.OA.OB =2p3a2; đường cao của hình chóp SO =a
2.
Thể tích khối chóp S.ABCD :VS.ABCD =1
3SABCD .SO =p3a3
3
Bài 1.3. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh bằng 3cm , các cạnh S A =
SB =SC =3cm. Tam giác SBD có diện tích bằng 6cm2.Tính thể tích của khối chóp S.ABCD.
Giải:
DA
CB
O
S
H
Gọi Hlà hình chiếu của Strên (ABCD)suy ra Hnằm trên BD (Vì S A =SB == SC,BD là trung
trực của AC). Do đó SH đường cao của hình chóp cũng là đường cao của tam giác SBD; Gọi O
là giao điểm của AC và BD.Vì S A =SC =D A =DC nên SO =DO suy ra tam giác SBD là tam
giác vuông tại S.Vì dt(SBD)=6và SB =3nên SD =4; suy ra BD =5,SH =12
5.
ABCD là hình thoi có AD =3,DO =5
2nên AO =p11
2suy ra dt(ABCD)=5p11
2.
http://boxmath.vn/ 2
VS.ABCD =1
3SH.dt(ABCD)=2p11.
Vậy thể tích khối chóp S.ABCD bằng 2p11(cm3).
Bài 1.4. Cho hình chóp S.ABC có S A =3a(với a>0); S A tạo với đáy (ABC)một góc bằng 600.
Tam giác ABC vuông tại B,
ACB =300.Glà trọng tâm tam giác ABC.Hai mặt phẳng (SGB)
và (SGC)cùng vuông góc với mặt phẳng (ABC).Tính thể tích hình chóp S.ABC theo a.
Giải:
A
C
B
K
G
S
Gọi Klà trung điểm BC.Ta có SG ⊥(ABC);
S AG =600,AG =3a
2.
Từ đó AK =9a
4;SG =3ap3
2.
Trong tam giác ABC đặt AB =x⇒AC =2x;BC =xp3.
Ta có AK2=AB2+BK2nên x=9ap7
14
Vậy VS.ABC =1
3SG.dt(ABC)=243
112 a3.
Bài 1.5. Cho hình chóp S.ABCD có đáy ABCD là hình vuông và tam giác S AB là tam giác
cân tại đỉnh S.Góc giữa đường thẳng S A và mặt phẳng đáy bằng 450, góc giữa mặt phẳng
(S AB)và mặt phẳng đáy bằng 600. Tính thể tích khối chóp S.ABCD,biết rằng khoảng cách
giữa hai đường thẳng CD và S A bằng ap6.
Giải:
A
BC
D
M
N
H
S
P
Gọi Hlà hình chiếu vuông góc của Slên mặt đáy, Mlà trung điểm AB và do tam giác S AB
cân tại Snên SM vuông góc với AB và kết hợp với SH vuông góc với đáy suy ra AB vuông góc
với mặt phẳng SMN nên theo giả thiết ta được: á
(S A,(ABCD)) =
S AH =450⇒S A =SHp2.
á
((S AB),(ABCD)) =á
(SM,MH)=
SMH =600⇒SM =SH.2
p3.
http://boxmath.vn/ 3
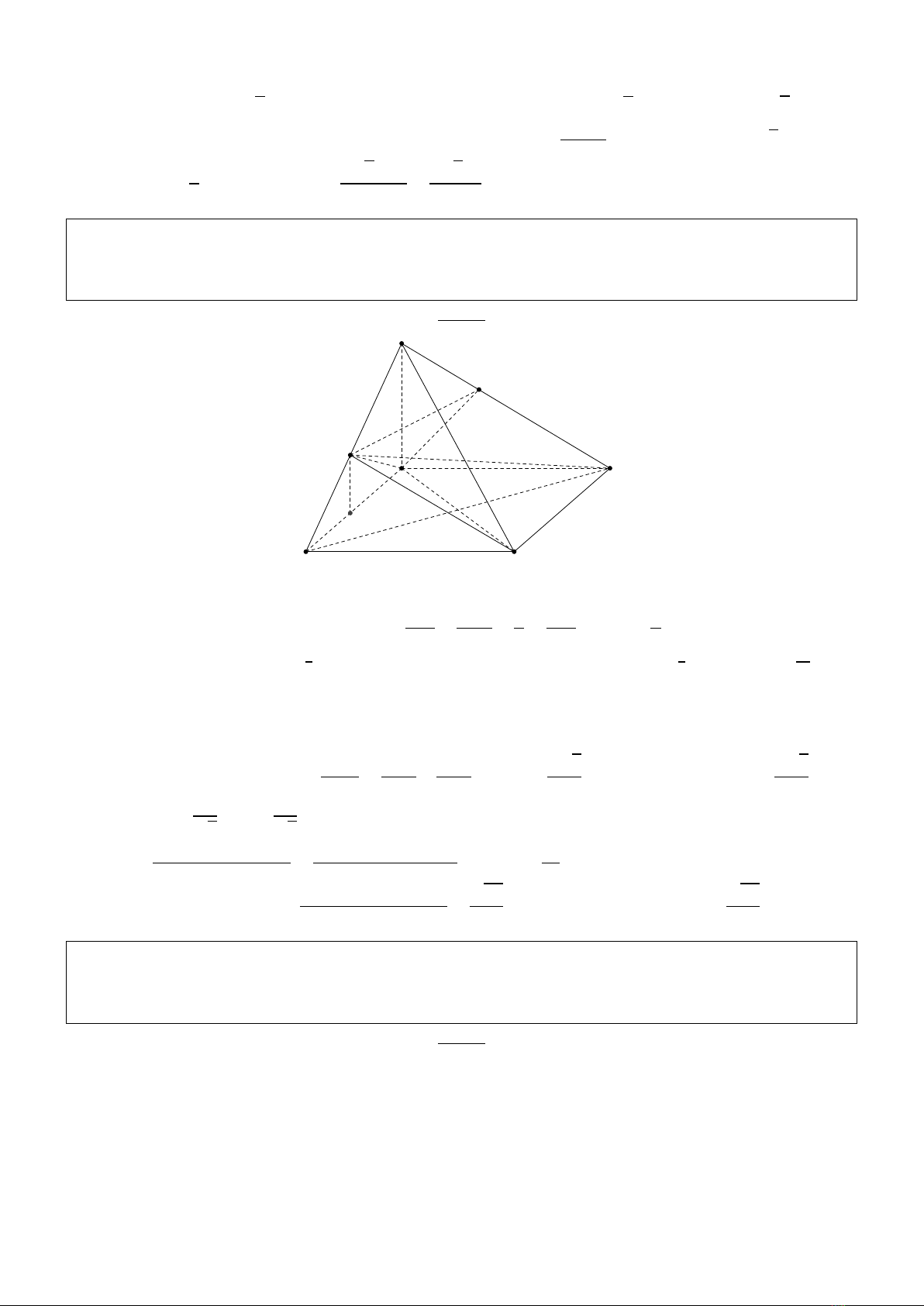
Từ điểm Nkẻ NP vuông góc với SM thì dễ thấy NP là khoảng cách giữa hai đường thẳng S A
và CD suy ra NP =ap6. Ta có SH.MN =NP.SM ⇐⇒ SH.AB =ap6.SH ⇐⇒ AB =2p2a
Trong tam giác S A M ta có S A2=AM2+SM2⇐⇒ 2.SH2=4SH2
3+2a2⇐⇒ SH =ap3.
Vậy VS.ABCD =1
3SH.dt(ABCD)=ap3.8a2
3=8p3a3
3.
Bài 1.6. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB =a,BC =2a.Cạnh bên
S A vuông góc với mặt đáy, S A =a.Gọi Hlà hình chiếu của Atrên SB.Tính thể tích khối
chóp H.ACD theo avà côsin của góc giữa hai mặt phẳng (SBC)và (SCD).
Giải:
A
BC
D
S
H
E
K
Kẻ HE//S A(E∈AB)⇒HE ⊥(ABCD).
Trong tam giác SAB có AB2=BH.SB ⇒BH
SB =AB2
SB2=1
2=HE
S A ⇒HE =a
2
Diện tích ∆ACD là S∆ACD =1
2AD.CD =a2⇒thể tích H.ACD là VH.ACD =1
3HE.S∆ACD =a3
6
S A ⊥(ABCD)⇒S A ⊥BC mà BC ⊥AB nên BC ⊥(S AB)⇒BC ⊥H A mà H A ⊥SB nên H A ⊥
(SBC)tương tự gọi Klà hình chiếu của Atrên SD thì AK ⊥(SCD)do vậy góc giữa hai mặt
phẳng (SBC)và (SCD)là góc giữa AH và AK.
trong tam giác vuông SAB có 1
AH2=1
AB2+1
S A2⇒AH =ap2
2,S A2=SH.SB ⇒SH =ap2
2
tương tự AK =2a
p5,SK =a
p5
cos
BSD =SB2+SD2−BD2
2.SB.SD =SH2+SK2−HK2
2.SH.SK ⇒HK2=a2
2
Trong ∆AHK có cos
AHK =AH2+AK2−HK 2
2.AH.AK =p10
5>0⇒cos(á
(SBC),(SCD)) =p10
5
Bài 1.7. Cho hình chóp S.ABCD có đáy ABCD là hình vuông . Mặt bên S AB là tam giác
cân tại S, mặt phẳng (S AB)vuông góc với đáy, mặt phẳng (SCD)tạo với đáy góc 600và cách
đường thẳng AB một khoảng là a.Tính thể tích khối chóp S.ABCD theo a.
Giải:
http://boxmath.vn/ 4
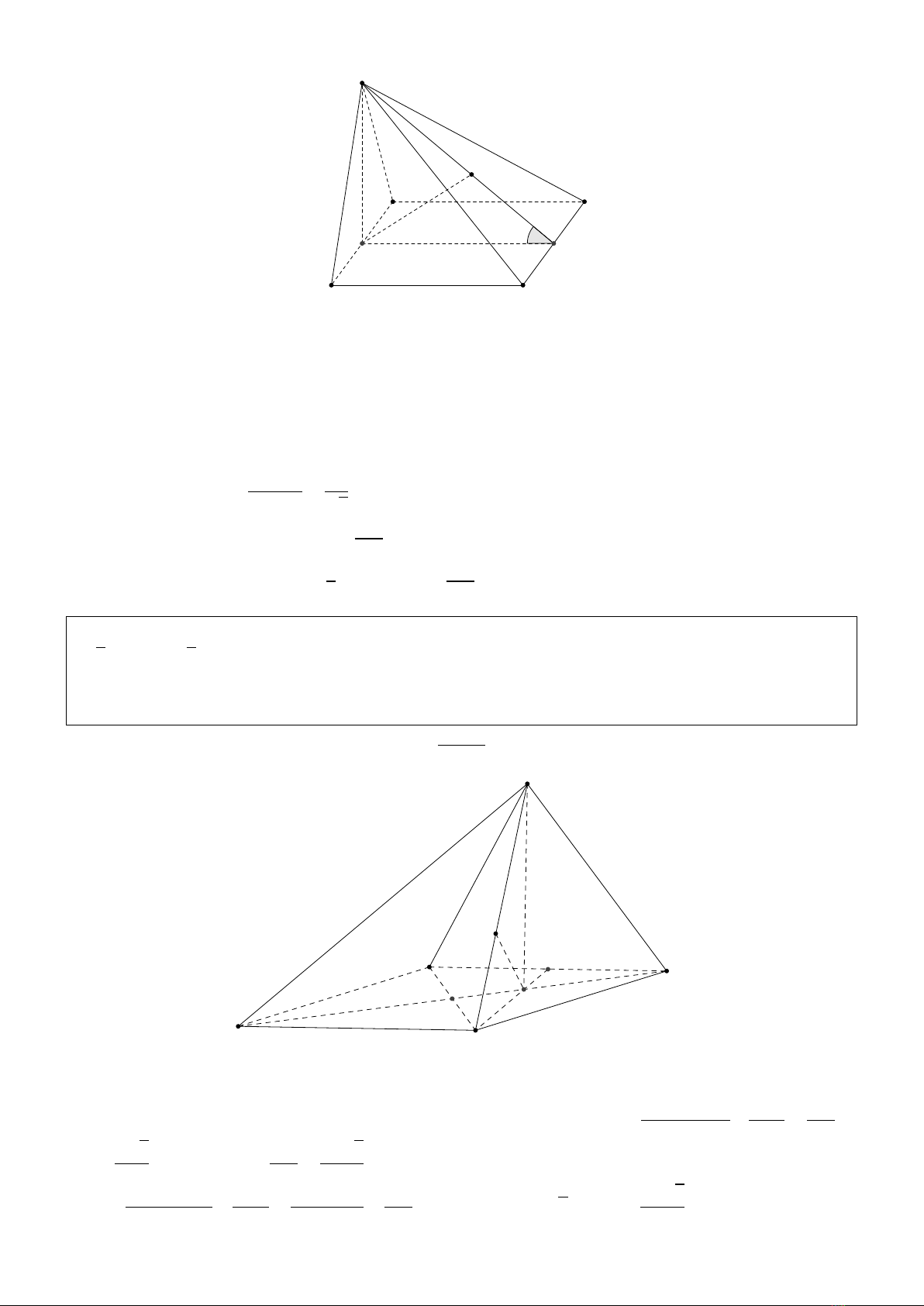
A
BC
D
H
I
S
K
Gọi H,Ilần lượt là trung điểm AB và CD Do S AB cân tại Snên SH ⊥AB mà (S AB)⊥(ABCD)
do đó SH ⊥(ABCD)⇒SH ⊥CD,H I ⊥CD nên CD ⊥(SHI), kẻ HK ⊥SI,CD ⊥HK nên HK ⊥
(SCD)⇒HK =d(H,(SCD)) =d(AB,(SCD)) =a
CD ⊥(SHI)⇒
HI⊥CD
SI⊥CD
CD =(SCD)∩(ABCD)
⇒(á
(SCD),(ABCD)=(à
HI,SI)=
SIH =600
Trong ∆HK I có HI =HK
sin600=2a
p3=BC. Trong ∆HSI có SH =HI.tan600=2a
diện tích ABCD là SABCD =BC2=4a2
3
Thể tích S.ABCD là VS.ABCD =1
3SH.SABCD =8a3
9.
Bài 1.8. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành thỏa mãn AB =2a,BC =
ap2,BD =ap6. Hình chiếu vuông góc của đỉnh Slên mặt phẳng (ABCD)là trọng tâm của
tam giác BCD.Tính theo αthể tích khối chóp S.ABCD, biết rằng khoảng cách giữa hai đường
thẳng AC và SB bằng a.
Giải:
D
C
AB
O
M
H
S
K
Gọi Hlà hình chiếu vuông góc của Slên mặt phẳng (ABCD),Mlà trung điểm CD và Olà tâm
của đáy ABCD. Do AO là trung tuyến của tam giác ABD nên AO2=AB2+AD2
2−BD2
4=3a2
2⇒
AO =ap6
2⇒AH =AO +AO
3=2ap6
3
BM2=BD2+BC2
2−CD2
4=6a2+2a2
2−4a2
4=3a2⇒BM =ap3⇒BH =2ap3
3
http://boxmath.vn/ 5