CH Đ PH NG TRÌNH -TOÁN 9Ủ Ề ƯƠ
A/ PH NG PHÁP XÉT KHO NG : ƯƠ Ả
+ N m bi t đ c ph ng pháp gi i ph ng trình ch a bi n trong d u giá tr tuy t đ i ắ ế ượ ươ ả ươ ứ ế ấ ị ệ ố
+ bi t đ c cách xét d u c a nh th c b c nh t ax + b đ ng d ng ế ượ ấ ủ ị ứ ậ ấ ể ứ ụ
vào vi c gi i ph ng trình ch a bi n trong d u giá tr tuy t đ i.ệ ả ươ ứ ế ấ ị ệ ố
I.KI N TH C B SUNGẾ Ứ Ổ
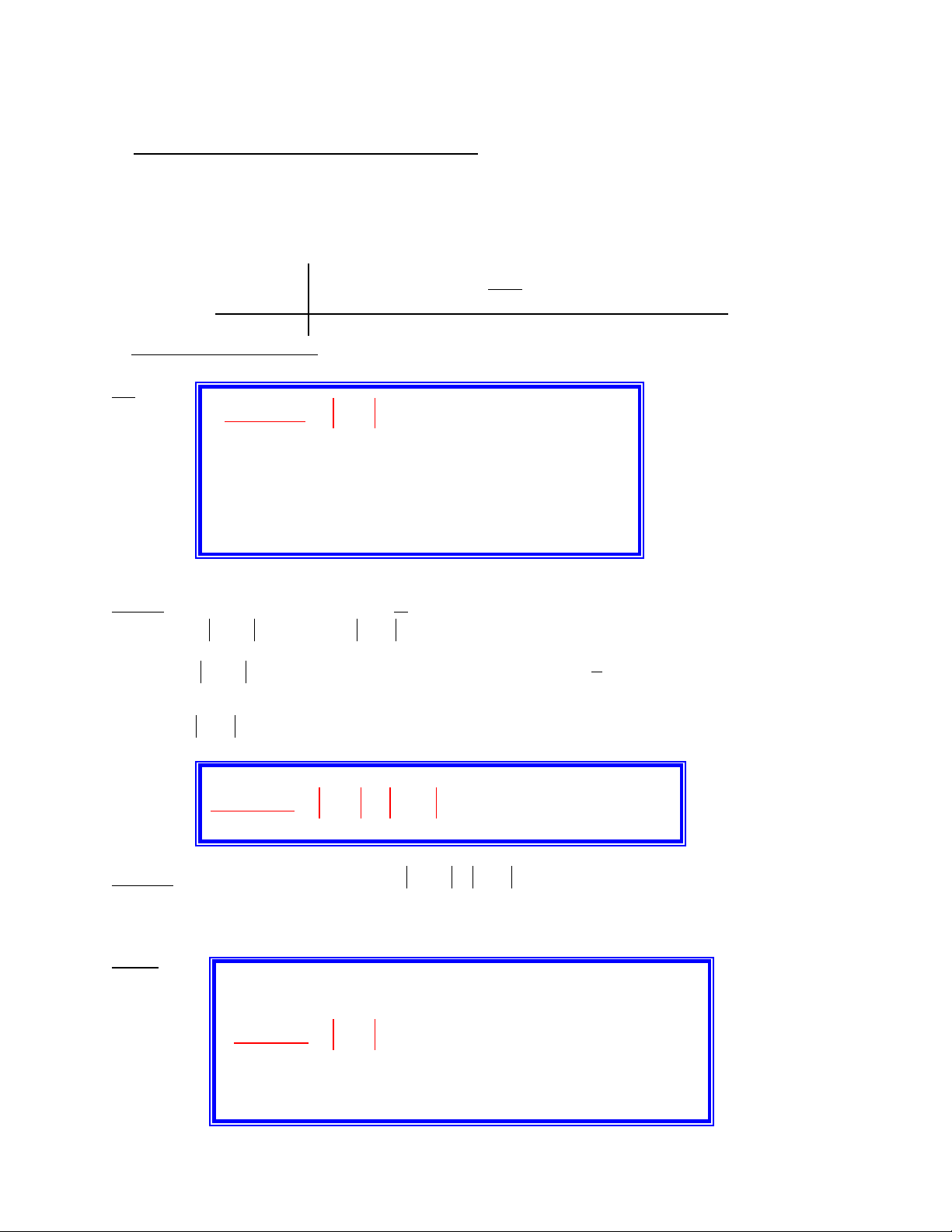
* D u c a nh th c b c nh t ax + bấ ủ ị ứ ậ ấ
x
a
b
−
ax + b Trái d u v i aấ ớ 0 Cùng d u v i aấ ớ
II.CÁC D NG BÀI T P Ạ Ậ
Ví d ụ1: Gi i các ph ng trình sauả ươ :
a)
2 1 0x− =
, b)
2 3x− =
gi i: ảa)
2 1 0x− =
2x – 1 = 0
x = ½ . V y : S = ậ
1
2
� �
� �
�
b)
2 3x− =
2 3
2 3
x
x
− =
− = −
5
1
x
x
=
= −
.V y : S = ậ
{ }
1;5−
Ví d 2ụ: Gi i các ph ng trình sauả ươ :
2 1 2x x− = −
2 1 2
2 1 2
x x
x x
− = −
− = − +
1
1
x
x
= −
=
. V y : S = ậ
{ }
1;1−
1
* D NG 1 :Ạ
f(x) = a
(1)
•a < 0 , ta có Pt (1) : vô nghi m ệ
•a = 0 , ta có Pt (1)
f(x) = 0
•a > 0 , ta có Pt (1)
f(x) = a
f(x) = -a
* D NG 2Ạ:
f(x) = g(x)
( )
( )
g x
g x
f(x) =
f(x) = -
* D NG 3Ạ:
f(x) = g(x)
�
f(x) 0
f(x) = g(x)
f(x) < 0
f(x) = -g(x)
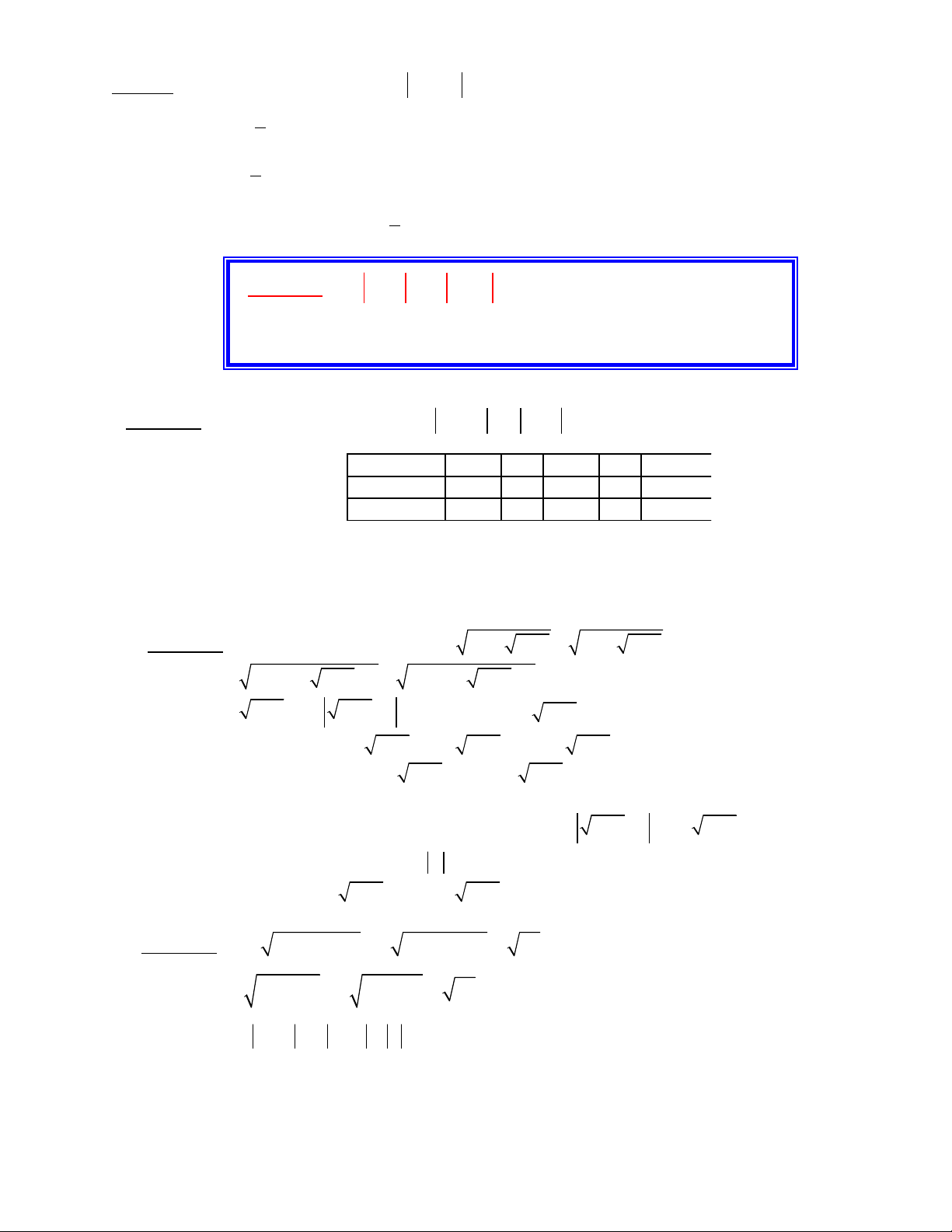
Ví d 3ụ: Gi i các ph ng trình sauả ươ :
3 2 2 6x x
− = +
+ V i x ớ
2
3
, ta có Pt : 3x – 2 = 2x + 6
x = 8 ( nh n)ậ
+ V i x < ớ
2
3
, ta có Pt : 3x – 2 = –2x – 6
x = - 4/5 ( nh n)ậ
V y : S = ậ
4;8
5
� �
−
� �
�
Ví d 4.1ụ: Gi i các ph ng trình sauả ươ :
2 1 3 1 1x x
− − − =
+ B ng xét d u : ả ấ
•V i x < ½ , ta có Pt : 1 – 2x ớ– 3( 1 – x ) = 1
x = 3 ( lo i )ạ
•V i ½ ớ
x < 1 , ta có Pt : 2x – 1 – 3(1 – x ) = 1
x = 1 ( lo i )ạ
•V i x ớ
1 , ta có Pt : 2x – 1 – 3(x – 1 ) = 1
x = 1 ( nh n )ậ
V y : S = ậ
{ }
1
Ví d 4.2ụ: Gi i các ph ng trình sauả ươ :
2 1 2 1 2x x x x+ − + − − =
; ĐK : x
1
1 2 1 1 1 2 1 1 2x x x x− + − + + − − − + =
1 1 1 1 2x x− + + − − =
(2) ; ( vì
1 1 0x−+>
)
* N u x > 2 thì Pt (2) ế
1x−
+1 +
1x−
- 1 = 2
1x−
= 1
x = 2 (lo i)ạ
* N u 1 ế
2x
thì Pt (2)
1x−
+1 + 1 -
1x−
= 2
0.x = 0 , Pt vô s nghi m ố ệ
V yậ Pt đã cho có nghi mệ 1
2x
+ Cách khác : Sau khi bi n đ i đ n Pt (2) ta có th vi t : ế ổ ế ể ế
1 1 1 1x x− − = − −
Chú ý b t đ ng th c ấ ẳ ứ
A A
v i đi u ki n x y ra ” =” là A ớ ề ệ ả
0 .
Vì th 1 - ế
1x−
0
1x−
1
x
2
K t h p v i ĐK ban đ u ta có ế ợ ớ ầ 1
2x
Ví d 4.2ụ: c)
2 2 2
6 9 2 2 1 0x x x x x+ + − − + + =
Giai : ⇔
( ) ( )
2 2 2
3 2 1 0x x x+ − − + =
⇔
3 2 1 0x x x+ − − + =
. (2)
+ N uế
3x
< −
, (2)⇒
( ) ( )
3 2 1 0x x x− + − − − − =� �
� �
⇔
0. 5 0x
− =
: vô nghi m.ệ
x 1/2 1
2x – 1 – 0 + +
X - 1 – – 0 +
2
* D NG 4Ạ:
( )a b h x
+ =
f(x) g(x)
+ Dùng b ng xét d u các giá tr bi n là nghi m c a các đa th cả ấ ị ế ệ ủ ứ
, đ kh d u giá tr tuy t đ i , r i gi i các Pt ể ử ấ ị ệ ố ồ ả

+ N u : ế
3 0x
− <
, (2)⇒
( ) ( )
3 2 1 0x x x+ − − − − =� �
� �
⇔
2 1 0x
+ =
⇔
1
2
x= −
.
+ N u : ế
0 1x
<
, (2)⇒
( ) ( )
3 2 1 0x x x+ − − − + =� �
� �
⇔
4 1 0x
+ =
⇔
1
4
x= −
, (lo i).ạ
+ N u ; ế
1x
, (2)⇒
( ) ( )
3 2 1 0x x x+ − − + =
⇔
0. 5 0x
− =
: vô nghi m.ệ
V y ph ng trình đã cho có m t nghi m ậ ươ ộ ệ
1
2
x= −
.
III. BÀI T P Đ NGHẬ Ề Ị
Gi i các ph ng trình sauả ươ : a)
2
2 1 5x x− + =
; b)
2
4 4 1 2x x x− + = −
c)
2 2
6 9 4 4 0x x x x− + + + + =
B/ PH NG PHÁP T NG CÁC S KHÔNG ÂMƯƠ Ổ Ố
+ S d ng đ c tính ch t t ng các s không âm đ v n d ng vào vi c gi i ph ng trình.ử ụ ượ ấ ổ ố ể ậ ụ ệ ả ươ
+ Nh n d ng và bi n đ i đ c các ph ng trình v d ng trên.ậ ạ ế ổ ượ ươ ề ạ
I.CÁC D NG BÀI T P :Ạ Ậ
Ví d 5ụ: Gi i các ph ng trình sauả ươ : 2x2 + 2x + 1 =
4 1x+
(*)
Gi i :ả ĐK : 4x + 1
0
x
- ¼
(*)
4x2 + 4x + 2 = 2
4 1x+
4x2 + 4x + 1 – 2
4 1x+
+1 = 0
4x2 + (
4 1x+
- 1 )2 = 0
( )
4 0
4 1 1
x
x o
=
+ − =
0
4 1 1
x
x
=
+ =
x = 0 ( nh n) . V y : S = ậ ậ
{ }
0
Ví d 5’ụ: Tìm các giá tr x, y, z bi t :ị ế
1
2 3 5 ( 7)
2
x y z x y z
− + − + − = + + −
(1)
+ ĐK : x
2 ; y
3 ; z
5
(1)
2 2 2 3 2 5 7 0x y z x y z
− + − + − − − − + =
2 2 2
( 2 1) ( 3 1) ( 5 1) 0x y z
− − + − − + − − =
2 1 0
3 1 0
5 1 0
x
y
z
− − =
− − =
− − =
3
4
6
x
y
z
=
=
=
3
* D NG 5 Ạ: A2 + B2 = 0
A = 0
B = 0
* D NG 6 Ạ:
A = 0
A + B = 0 B = 0

Ví d 6 ụ: Gi i các ph ng trình sauả ươ :
2
1 3 2 0x x x− + − + =
(**)
(**)
2
1 0
3 2 0
x
x x
− =
− + =
1 0
( 1)( 2) 0
x
x x
− =
− − =
1
1
2
x
x
x
=
=
=
x = 1 . V y : S = ậ
{ }
1
Ví d 7 ụ: Gi i các ph ng trình sauả ươ :
2
2 1 1 0x x x− + + − =
2
1 0
2 1 0
x
x x
− =
− + =
2
1 0
( 1) 0
x
x
− =
− =
x =1 . V y : S = ậ
{ }
1
II.BÀI T P Đ NGHẬ Ề Ị
Gi i các ph ng trình sauả ươ :
a)
1
1 2 ( )
2
x y z x y z+ − + − = + +
; b) x + y + 4 = 2
x
+ 4
1y−
;
c) x + y + z + 4 =
2 2 4 3 6 5x y z− + − + −
; d )
2 2
9
3 2 1 0
4
x x x x+ + + + + =
C. PH NG PHÁP Đ I L P VÀ B T Đ NG TH C :ƯƠ Ố Ậ Ấ Ẳ Ứ
+ S d ng đ c tính ch t đ i l p hai v c a ph ng trình.ử ụ ượ ấ ố ậ ở ế ủ ươ
+ Ngoài nh ng b t đ ng th c c a các s không âm bài tr c , c n n m ữ ấ ẳ ứ ủ ố ở ướ ầ ắ
thêm và s d ng m t s b t đ ng th c quen thu c nh BĐT Cô Si; ử ụ ộ ố ấ ẳ ứ ộ ư
BĐT Svacx ; BĐT v giá tr tuy t đ i vào vi c gi i ph ng trình.ơ ề ị ệ ố ệ ả ươ
I/KI N TH C C B NẾ Ứ Ơ Ả
1_ S d ng tính ch t tính ch t đ i ngh ch giá tr c a hai v Pt :ử ụ ấ ấ ố ị ị ủ ế
Ví d 8 ụ: Gi i các ph ng trình sauả ươ :
a)
2 2 2
3 6 7 5 10 14 4 2x x x x x x
+ + + + + = − −
2 2 2
3( 1) 4 5( 1) 9 5 ( 1)x x x
+ + + + + = − +
Mà (VT) =
2 2
3( 1) 4 5( 1) 9 4 9 5x x
+ + + + + + =
,
d u”=” x y ra khi (x + 1)ấ ả 2 = 0
x = -1
Và (VP) = 5 – (x + 1)2
5 , d u “=” x y ra khi (x + 1)ấ ả 2 = 0
x = -1
Do đó :
2 2 2
3 6 7 5 10 14 4 2 5x x x x x x
+ + + + + = − − =
(x + 1)2 = 0
x = -1 . V y : S = ậ
{ }
1−
b)
2
7 9 16 66x x x x− + − = − +
; ĐK :
7 9x
(VT) : A =
7 9x x− + −
A2 = 2 + 2
( 7)(9 ) 2 7 9 4x x x x− − + − + − =
4
* D NG 7 Ạ:
A = 0
A + B = 0 B = 0
* D NG 8 Ạ:
A m
B m
A = B
A = m
B = m
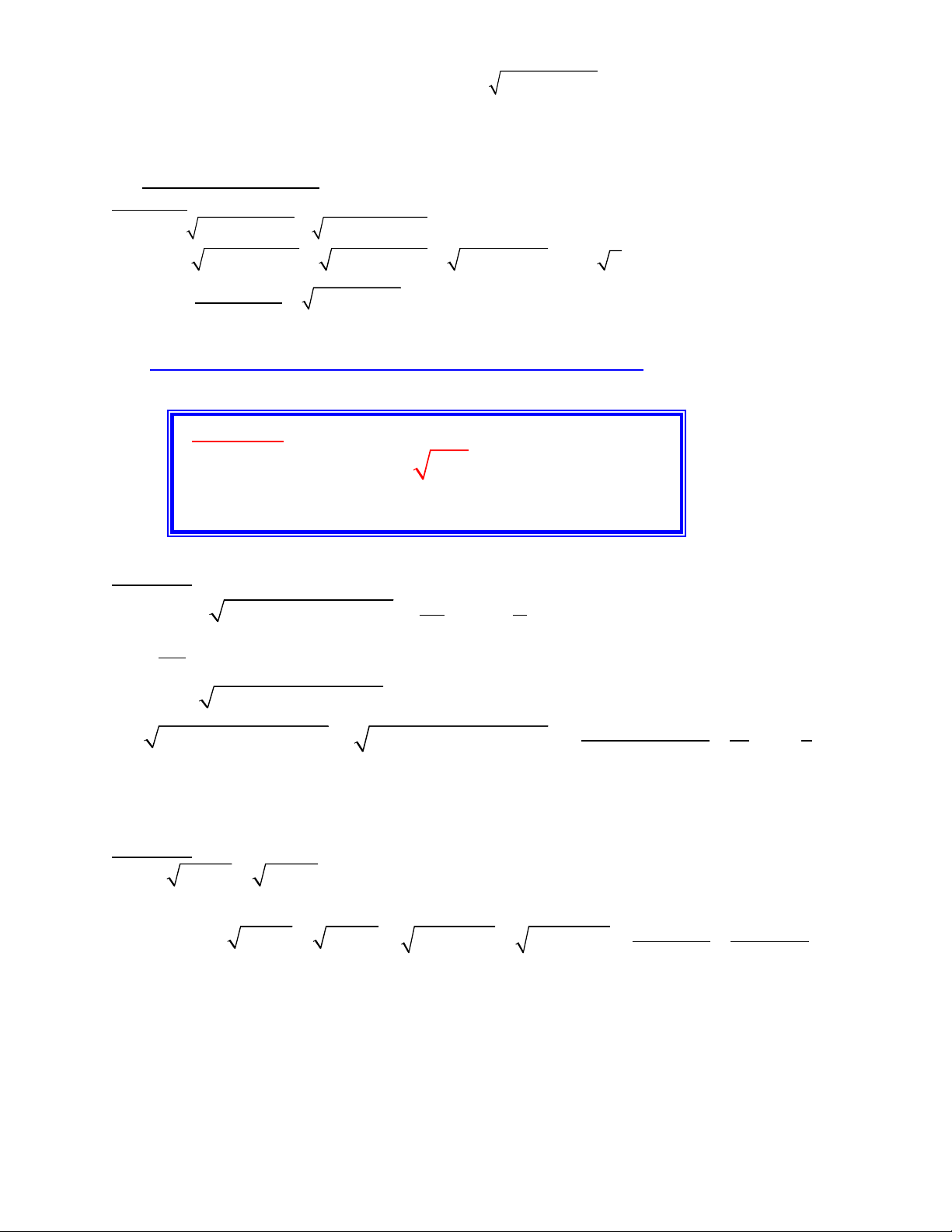
(Áp d ng BĐT Cô Si 2ụ
( 7)(9 ) 2 7 9 4x x x x− − + − + − =
)
Do đó A
2
(VP) : B =
2
16 66x x− +
= (x – 8 )2 + 2
2
Theo đ bài A = B nên A = B = 2 . Do đó x – 7 = 9 – x ; x = 8 (nh n)ề ậ
II. BÀI T PẬ Đ NGHỀ Ị
Ví d 18 ụ: Gi i các ph ng trình sauả ươ :
a)
2 4 2 2
3 6 12 5 10 9 3 4 2x x x x x x+ + + − + = − −
b)
2 2 2
6 11 6 13 4 5 3 2x x x x x x
− + + − + + − + = +
c)
2
2
2
6 15 6 18
6 11
x x x x
x x
− + = − +
− +
2_ S d ng b t đ ng th c CÔ-SI cho hai s không âmử ụ ấ ẳ ứ ố
Ví d 9.1 ụ: Gi i các ph ng trình sauả ươ :
2
3 2
1
5 3 3 2 3
2 2
x
x x x x
+ + − = + −
ĐK : Vì 5x3 + 3x2 + 3x – 2 = (x2 + x + 1) (5x – 2)
Mà x2 + x + 1 = (x + ½)2 + ¾ > 0
nên
3 2
5 3 3 2x x x
+ + −
có nghĩa khi 5x – 2
x
2/5
3 2 2
5 3 3 2 ( 1)(5 2)x x x x x x
+ + − = + + −
2 2
1 5 2 1
3
2 2 2
x x x x x
+ + + − = + −
( theo BĐT Cô-Si cho hai s không âm)ố
D u “ = ” x y ra khi xấ ả 2 + x + 1 = 5x – 2
x2 – 4x + 3 = 0
(x – 1)(x – 3) = 0
x = 1 ; x = 3 . V y : S = ậ
{ }
1;3
Ví d 9.2 ụ: Gi i các ph ng trình sauả ươ :
2
2 3 5 2 3 12 14x x x x
− + − = − +
Áp d ng BĐT Cô-Si cho hai s không âm ta có :bụ ố
2 3 1 5 2 1
2 3 5 2 (2 3).1 (5 2 ).1 2
2 2
x x
x x x x
− + − +
− + − = − + − + =
D u “ = ” x y ra khi ấ ả
2 3 0
5 2 0
x
x
− =
− =
x = 2
M t khác 3xặ2 – 12x +14 = 3(x2 – 4x + 4) + 2 = 3(x – 2)2 + 2
2
D u “ = ” x y ra khi x – 2 = 0 ấ ả
x = 2
V y Pt có nghi m duy nh t x = 2 ậ ệ ấ
3_ S d ng b t đ ng th c SVAC Xử ụ ấ ẳ ứ Ơ
5
* D NG 9 Ạ : V i hai s a ,b không âm ta có : ớ ố
a + b 2 a.b
D u “=” x y ra khi a = b ấ ả
















