trÇn quang thanh-k15-ch-lý-®h-vinh-8-2008
1
PHÇN I
C¸CH CHøNG MINH C¤NG THóC TÝNH VËN TèC Vµ SøC C¡NG D¢Y
CñA CON L¾C §¥N
PH¦¥NG PH¸P:
1. C«ng thøc tÝnh vËn tèc t¹i vÞ trÝ bÊt kú:
Do con l¾c chuyÓn ®éng trong tr−êng träng lùc nªn c¬ n¨ng b¶o toµn
Chän mèc thÕ n¨ng h=o t¹i vÞ trÝ c©n b»ng O. ¸p dông ®Þnh luËt
B¶o toµn c¬ n¨ng cho 2 vÞ trÝ A vµ B ta cã
. W
A
=W
B
hay :
2
.
2
B
A B
m v
mgh mgh= +
(1)
Chó ý : con l¾c ®¬n ®−îc th¶ kh«ng vËn tèc ban ®Çu tõ vÞ trÝ A
Nªn v
A
=O
Trong ®ã
. . ( )
A o
h IO IH l l co s
= − = −
. . ( )
B
h IO IB l l co s
α
= − = −
Nªn thay vµo biÓu thøc (1) ta cã:
2
.
[ . ( )] [ . ( )]
2
B
o
m v
mg l lco s mg l lco s
α α
− = − +
T−¬ng ®−¬ng :
[
]
2. . . ( ) . ( )
B o
v g l co s co s
α α
= −
(2)
Tõ ®ã ta cã c¸c tr−êng hîp sau x¶y ra :
a. T¹i vÞ trÝ c©n b»ng gãc
0
o
α
=
cos(o
o
)=1
suy ra
[
]
.
2. . 1 . ( )
ma x o
v g l co s
α
= −
(3) ( T¹i VTCB vËn tèc ®¹t gi¸ trÞ cùc ®¹i )
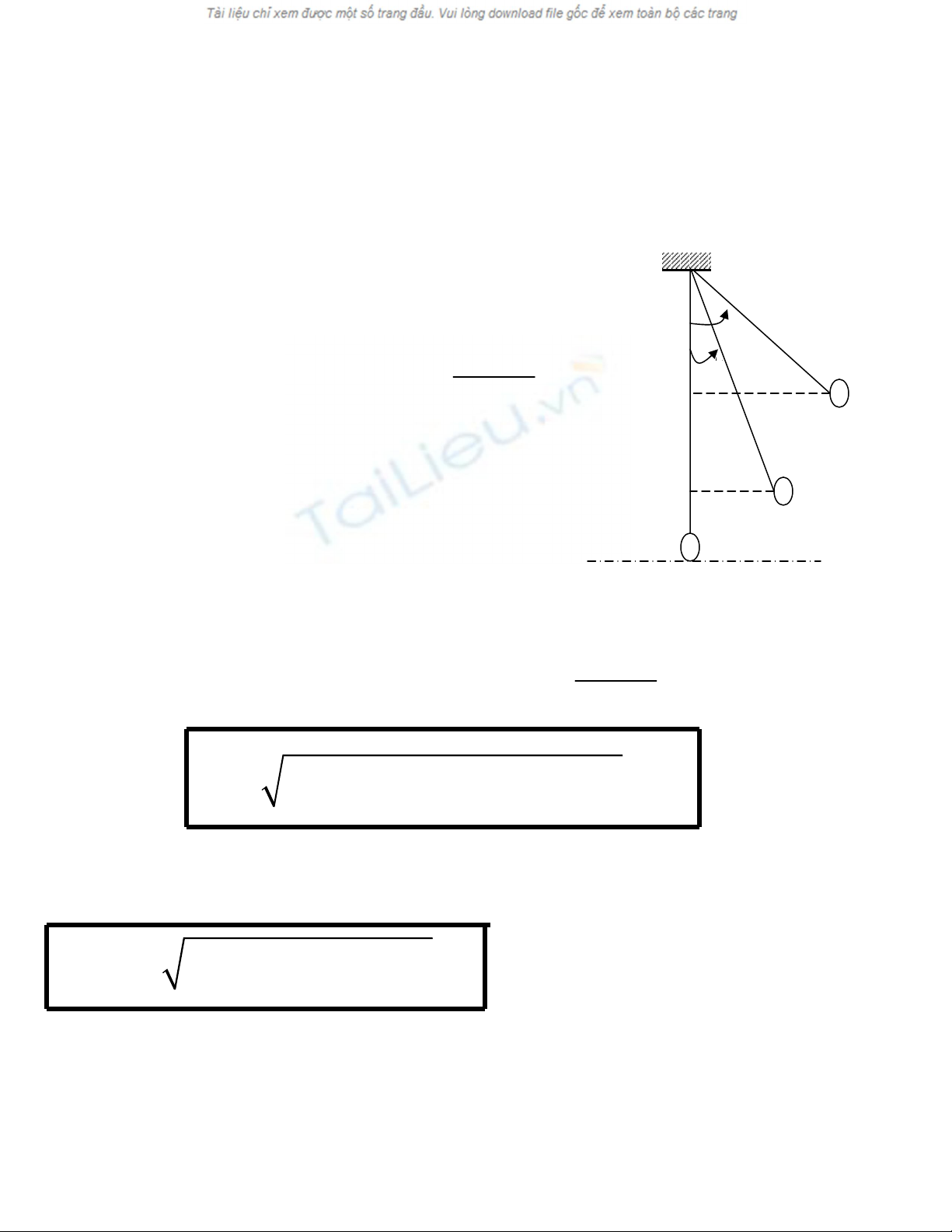
I
O
α
O
B
A
α
O
α
A
H
B
trÇn quang thanh-k15-ch-lý-®h-vinh-8-2008
2
N
NÕ
Õu
u
g
gã
ãc
c
0 0
10 , 10
o
α α
≤ ≤
ta sö dông c«ng thøc gÇn ®óng :
2
2
. ( ) 1 2.sin 1
2 2
co s
α α
α
= − ≈ −
Vµ
2
2
0 0
0
. ( ) 1 2.sin 1
2 2
co s
α α
α
= − ≈ −
Thay tÊt c¶ vµo (2) ta cã :
2 2
0
.
B
v g l
α α
= −
(
(4
4)
)
V
Vµ
µ
c
c«
«n
ng
g
t
th
hø
øc
c
v
vË
Ën
n
t
tè
èc
c
c
cù
ùc
c
®
®¹
¹i
i
l
ló
óc
c
n
nµ
µy
y
l
lµ
µ
:
:
t
th
ha
ay
y
v
vµ
µo
o
(
(3
3)
)
:
:
2 2
0 0
.
2. . 1 (1 2.sin ) 2. . 2.sin
2 2
ma x
v g l g l
α α
= − − =
2
0
. 0
2. . .2. . .
4
ma x
v g l g l
αα
≈ =
(5) Do
2
2
0 0
sin
2 4
α α
≈
T¹i vÞ trÝ biªn
0
α α
=
nªn .minB
v o
=
2
2.
.C
C«
«n
ng
g
t
th
hø
øc
c
t
tÝ
Ýn
nh
h
s
sø
øc
c
c
c¨
¨n
ng
g
d
d©
©y
y
T
T
t
t¹
¹i
i
v
vÞ
Þ
t
tr
rÝ
Ý
b
bÊ
Êt
t
k
kú
ú
:
:
x
xÐ
Ðt
t
t
t¹
¹i
i
v
vÞ
Þ
t
tr
rÝ
Ý
b
bi
iª
ªn
n
A
A
t
ta
a
c
cã
ã
c
c¸
¸c
c
l
lù
ùc
c
t
t¸
¸c
c
d
dô
ôn
ng
g
l
lª
ªn
n
v
vË
Ët
t
m
m
l
lµ
µ
s
sø
øc
c
c
c¨
¨n
ng
g
s
sî
îi
i
d
d©
©y
y
T
T
v
vµ
µ
t
tr
rä
än
ng
g
l
lù
ùc
c
P
P.
.
T
Th
he
eo
o
®
®Þ
Þn
nh
h
l
lu
uË
Ët
t
I
II
I
N
NI
IU
UT
T¥
¥N
N
t
ta
a
c
cã
ã
:
:
.
P T m a
+ =
(
(6
6)
)
trÇn quang thanh-k15-ch-lý-®h-vinh-8-2008
3
C
Ch
hi
iÕ
Õu
u
(
(6
6)
)
l
lª
ªn
n
p
ph
h−
−¬
¬n
ng
g
s
sî
îi
i
d
d©
©y
y
h
h−
−í
ín
ng
g
v
vµ
µo
o
®
®i
iÓ
Óm
m
t
tr
re
eo
o
I
I
c
ch
hi
iÒ
Òu
u
d
d−
−¬
¬n
ng
g
n
nh
h−
−
h
h×
×n
nh
h
v
vÏ
Ï
:
:
2
. ( ) .
B
v
Pco s T m
l
α
− + =
(
(7
7)
)
T
Th
ha
ay
y
(
(2
2)
)
v
vµ
µo
o
(
(7
7)
)
:
:
[
]
0
3. . ( ) 2. . ( )
T mg co s co s
α α
= −
(
(8
8)
)
T
T¹
¹i
i
V
VT
TC
CB
B
0
o
α
=
cos(o
o
)=1 nªn :
[
]
. 0
3 2. . ( )
ma x
T mg co s
α
= −
(
(9
9)
)
T
T¹
¹i
i
v
vÞ
Þ
t
tr
rÝ
Ý
h
ha
ai
i
b
bi
iª
ªn
n
0
α α
=
nªn :
[
]
min 0
. ( ) . . ( )
T mg co s mg co s
α α
= =
(
(1
10
0)
)
N
NÕ
Õu
u
g
gã
ãc
c
0 0
10 , 10
o
α α
≤ ≤
ta sö dông c«ng thøc gÇn ®óng :
2
2
. ( ) 1 2.sin 1
2 2
co s
α α
α
= − ≈ −
Vµ
2
2
0 0
0
. ( ) 1 2.sin 1
2 2
co s
α α
α
= − ≈ −
Suy ra :
2
2 2
2
0
0
3(1 ) 2.(1 ) . 1 3.
2 2 2
T mg mg
α
α α α
≈ − − − = − +
T
T¹
¹i
i
V
VT
TC
CB
B
0
o
α
=
cos(o
o
)=1 nªn : (11)
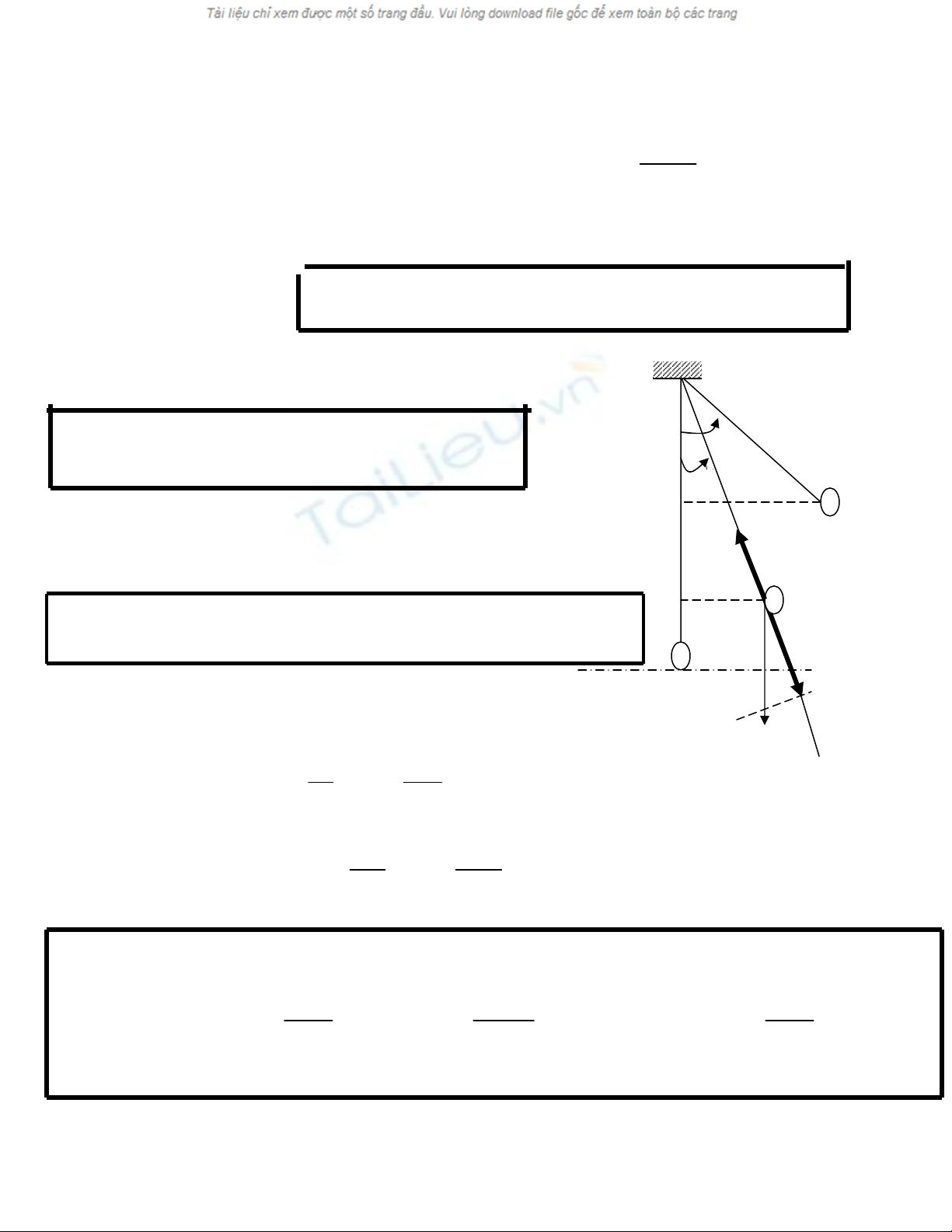
P
X
P
α
O
B
A
α
O
α
A
H
B
T
I
T
trÇn quang thanh-k15-ch-lý-®h-vinh-8-2008
4
[ ]
2
0
. 0
3 2. . ( ) . 3 2.(1 )
2
ma x
T mg co s mg
α
α
= − = − −
H
Ha
ay
y
:
:
2
. 0
1
ma x
T mg
α
= +
(
(1
12
2)
)
T
T¹
¹i
i
v
vÞ
Þ
t
tr
rÝ
Ý
h
ha
ai
i
b
bi
iª
ªn
n
0
α α
=
nªn :
[ ]
2
2
0
min 0
. ( ) . . ( ) .(1 ) .(1 )
2 2
T mg co s mg co s mg mg
α
α
α α
= = ≈ − = −
P
PH
HÇ
ÇN
N
2
2
(
(1
13
3)
)
B
Bi
iÕ
Õn
n
t
th
hi
iª
ªn
n
c
ch
hu
u
k
kú
ú
c
cñ
ña
a
c
co
on
n
l
l¾
¾c
c
®
®¬
¬n
n
t
th
he
eo
o
n
nh
hi
iÖ
Öt
t
®
®é
é,
,
®
®é
é
c
ca
ao
o
v
vµ
µ
v
vÞ
Þ
t
tr
rÝ
Ý
t
tr
rª
ªn
n
t
tr
r¸
¸i
i
®
®Ê
Êt
t
P
PH
H¦
¦¥
¥N
NG
G
P
PH
H¸
¸P
P
:
:
D
Dù
ùa
a
v
vµ
µo
o
c
c«
«n
ng
g
t
th
hø
øc
c
:
:
0
(1 . )
2 . 2.
l t
l
Tg g
α
π π
+
= =
T
Tr
ro
on
ng
g
®
®ã
ã
:
:
o
l
:
:
l
lµ
µ
c
ch
hi
iÒ
Òu
u
d
dµ
µI
I
d
d©
©y
y
t
tr
re
eo
o
c
co
on
n
l
l¾
¾c
c
ë
ë
0
0
0
t c
=
l
:
:
l
lµ
µ
c
ch
hi
iÒ
Òu
u
d
dµ
µI
I
d
d©
©y
y
t
tr
re
eo
o
c
co
on
n
l
l¾
¾c
c
ë
ë
0
t c
α
:
:
l
lµ
µ
h
hÖ
Ö
s
sè
è
n
në
ë
d
dµ
µI
I
ë
ë
0
0
0
0
C
C
B
Bµ
µi
i
t
to
o¸
¸n
n
1
1
:
:
X
X¸
¸c
c
®
®Þ
Þn
nh
h
t
th
hê
êi
i
g
gi
ia
an
n
c
co
on
n
l
l¾
¾c
c
c
ch
h¹
¹y
y
s
sa
ai
i
t
tr
ro
on
ng
g
m
mç
çi
i
c
ch
hu
u
k
kú
ú.
.
T
TH
H1
1:
:
K
Kh
hi
i
ë
ë
®
®é
é
c
ca
ao
o
n
nh
hÊ
Êt
t
®
®Þ
Þn
nh
h
(
(c
cï
ïn
ng
g
®
®«
«
c
ca
ao
o
)
)
c
cã
ã
g
g=
=c
co
on
ns
st
t
v
vµ
µ
n
nh
hi
iÖ
Öt
t
®
®é
é
k
kh
h¸
¸c
c
n
nh
ha
au
u
(
(
1 2
t t
≠
)
)
C
Co
on
n
l
l¾
¾c
c
c
ch
h¹
¹y
y
®
®ó
ón
ng
g
ë
ë
n
nh
hi
iÖ
Öt
t
®
®é
é
t
t
1
1
,
,
t
ta
a
c
cã
ã
c
ch
hu
u
k
kú
ú
T
T
1
1
trÇn quang thanh-k15-ch-lý-®h-vinh-8-2008
5
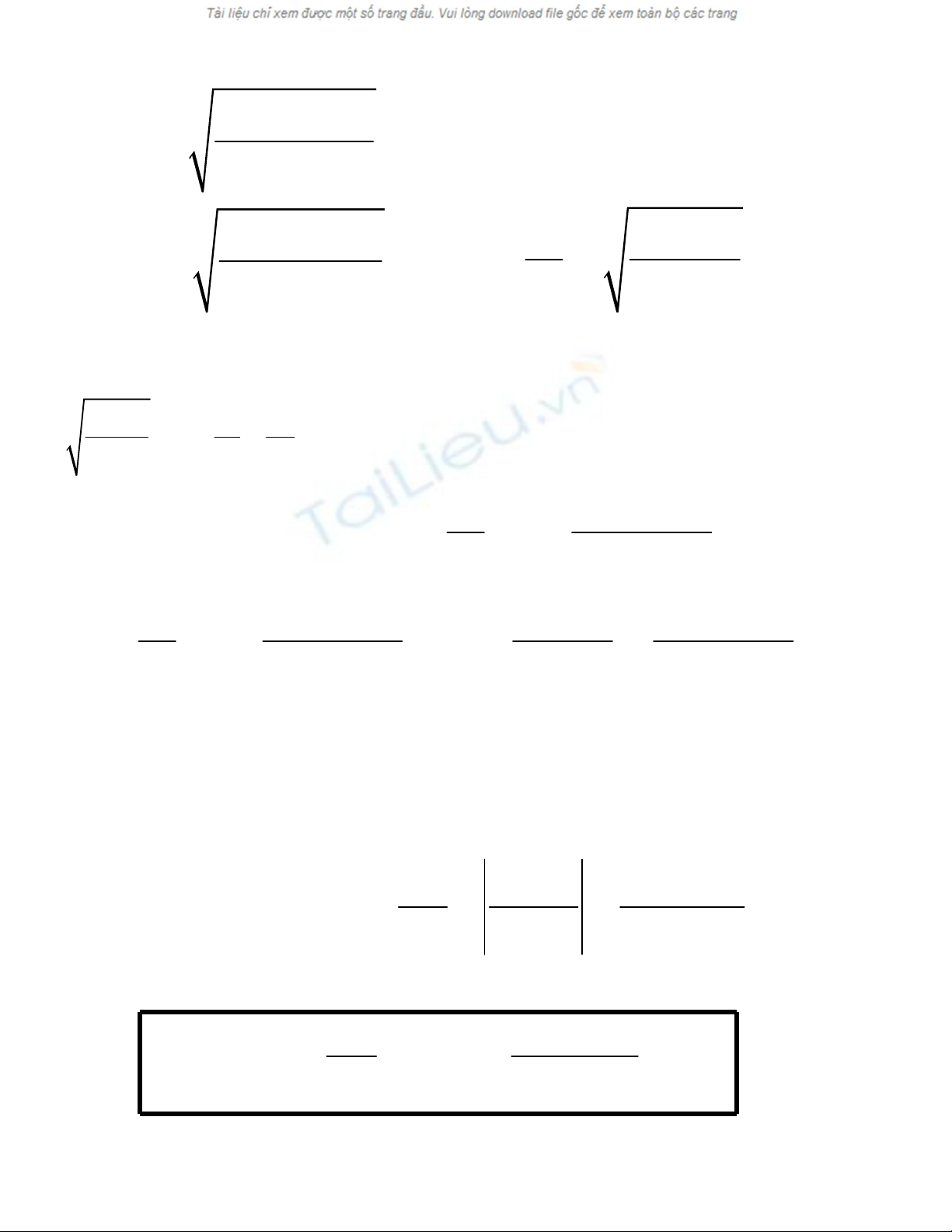
0 1
1
(1 . )
2.
l t
Tg
α
π
+
=
V
Vµ
µ
c
ch
hu
u
k
ký
ý
T
T
2
2
0 2
2
(1 . )
2.
l t
Tg
α
π
+
=
S
Su
uy
y
r
ra
a
:
:
1 1
2 2
1 .
1 .
T t
T t
α
α
+
=+
(
(1
14
4)
)
H
Ha
ay
y
:
:
¸
¸p
p
d
dô
ôn
ng
g
c
c«
«n
ng
g
t
th
hó
óc
c
g
gÇ
Çn
n
®
®ó
ón
ng
g
:
:
v
ví
íi
i
0 1
ε
< ≤
t
th
h×
×
:
:
1 1 2
2
11
1 2 2
ε ε ε
ε
+
≈ + −
+
(
(1
15
5)
)
t
th
ha
ay
y
(
(1
15
5)
)
v
vµ
µo
o
(
(1
14
4)
)
t
ta
a
c
cã
ã
1 1 2
2
( )
12
T t t
T
α
−
≈ +
H
Ha
ay
y
1 1 2
2
( )
12
T t t
T
α
−
− ≈
⇔
1 2 1 2
2
( )
2
T T t t
T
α
− −
≈
(
(1
16
6)
)
N
NH
HË
ËN
N
X
XÐ
ÐT
T:
:
+
+)
)N
NÕ
Õu
u
t
t
1
1
>
>t
t
2
2
s
su
uy
y
r
ra
a
T
T1
1>
>T
T2
2
c
ch
hu
u
k
kú
ú
g
gi
i
m
m
®
®å
ån
ng
g
h
hå
å
c
ch
h¹
¹y
y
n
nh
ha
an
nh
h.
.
+
+)
)N
N
Õ
Õu
u
t
t
1
1
<
<t
t
2
2
s
su
uy
y
r
ra
a
T
T
1
1
<
<T
T
2
2
c
ch
hu
u
k
kú
ú
t
t¨
¨n
ng
g
®
®å
ån
ng
g
h
hå
å
c
ch
h¹
¹y
y
c
ch
hË
Ëm
m
.
.
+
+)
)§
§é
é
b
bi
iÕ
Õn
n
t
th
hi
iª
ªn
n
t
t−
−¬
¬n
ng
g
®
®è
èi
i
t
tr
ro
on
ng
g
m
mç
çi
i
c
ch
hu
u
k
kú
ú
l
lµ
µ:
:
T
Tõ
õ
(
(1
16
6)
)
s
su
uy
y
r
ra
a
1 2 1 2
2 2
( )
2
T T t t
T
T T
α
− −
∆= =
(
(1
17
7)
)
K
KÕ
Õt
t
l
lu
uË
Ën
n
:
:
M
Mç
çi
i
n
ng
gµ
µy
y
®
®ª
ªm
m
®
®å
ån
ng
g
h
hå
å
c
ch
h¹
¹y
y
s
sa
ai
i
m
mé
ét
t
k
kh
ho
o
n
ng
g
1 2
2
( )
86400. 86400. 2
t t
T
T
α
θ
−
∆
= =
(
(1
18
8)
)