Toán 6 – H c Kì I – Nguy n Văn Quy n – 0938.59.6698 – s u t m và biên so nọ ễ ề ư ầ ạ
CHUYÊN Đ 1Ề
ĐI M, ĐNG TH NG, ĐO N TH NG, TIAỂ ƯỜ Ẳ Ạ Ẳ
TRUNG ĐI M ĐO N TH NGỂ Ạ Ẳ
A. Lý thuy tế
1. Đi mể
Hình nh c a đi m: m t d u ch m nh .ả ủ ể ộ ấ ấ ỏ
Ng i ta dùng các ch cái in hoa A, B, C, ... đ đt tên cho đi m.ườ ữ ể ặ ể
2. Đng th ngườ ẳ
S i ch căng th ng, mép b ng, ... cho ta hình nh c a đng th ng. ợ ỉ ẳ ả ả ủ ườ ẳ
Đng th ng không b gi i h n v hai phía. Có nh ng đi m thu c đng ườ ẳ ị ớ ạ ề ữ ể ộ ườ
th ng, có nh ng đi m không thu c đng th ng. ẳ ữ ể ộ ườ ẳ
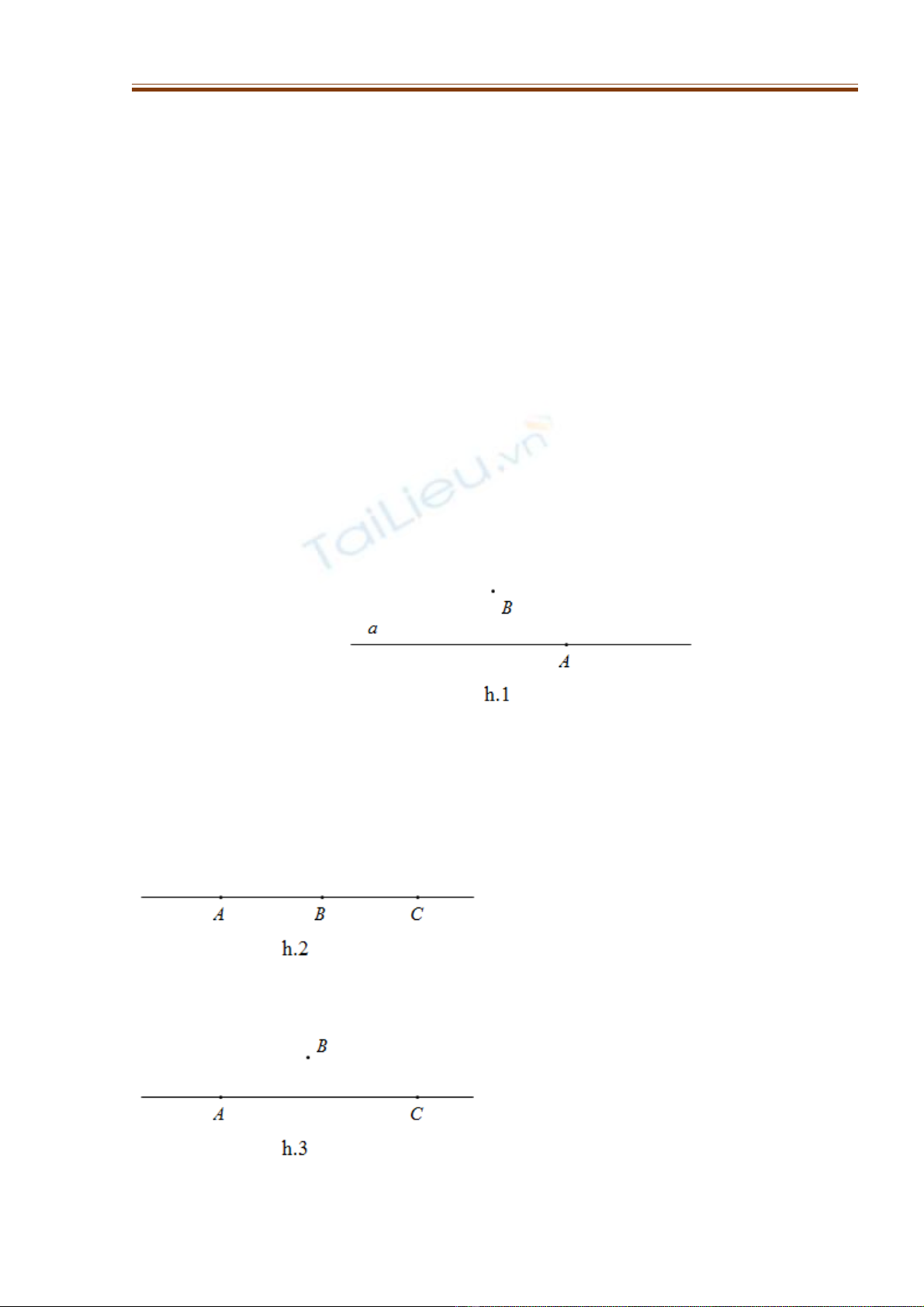
V trí c a đi m và đng th ng (h.1)ị ủ ể ườ ẳ
Đi m A thu c đng th ng a, kí hi u ể ộ ườ ẳ ệ
Đi m B không thu c đng th ng a, kí hi u ể ộ ườ ẳ ệ
3. Ba đi m th ng hàngể ẳ
Ba đi m A, B, C cùng thu c m t ể ộ ộ
đng th ng, ta nói chúng th ng ườ ẳ ẳ
hàng (h.2). Trong ba đi m th ng ể ẳ
hàng có m t và ch m t đi m ộ ỉ ộ ể
n m gi a hai đi m còn l i. ằ ữ ể ạ
Ba đi m A, B, C không cùng ể
thu c m t đng th ng, ta nói ộ ộ ườ ẳ
chúng không th ng hàng (h.3) . ẳ
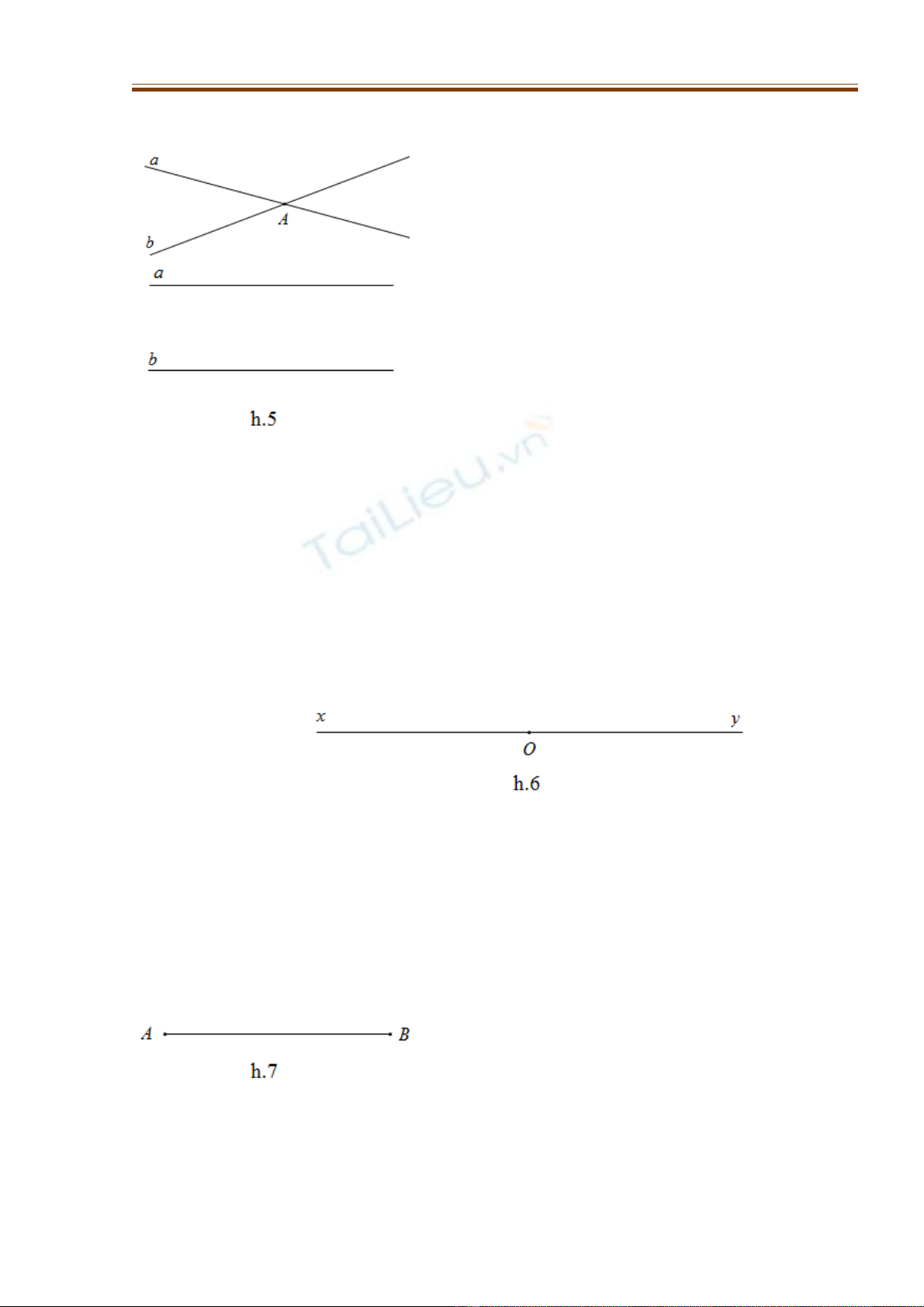
4. Đng th ng đi qua hai đi mườ ẳ ể
Toán 6 – H c Kì I – Nguy n Văn Quy n – 0938.59.6698 – s u t m và biên so nọ ễ ề ư ầ ạ
Có m t và ch m t đng th ng đi qua hai đi m A, B.ộ ỉ ộ ườ ẳ ể
Hai đng th ng ch có m t đi m ườ ẳ ỉ ộ ể
chung A ta nói chúng c t nhau và A ắ
là giao đi m c a hai đng th ng ể ủ ườ ẳ
đó (h.4).
Hai đng th ng không có đi m ườ ẳ ể
chung nào (dù kéo dài mãi v hai ề
phía) ta nói chúng song song (h.5).
Hai đng th ng không trùng nhau là hai đng th ng phân bi t. ườ ẳ ườ ẳ ệ
Hai đng th ng phân bi t ho c ch có m t đi m chung ho c khôngườ ẳ ệ ặ ỉ ộ ể ặ
có đi m chung nào. ể
5. Tia
Hình g m đi m O và m t ph n đng th ng chia ra b i O là m t tia g c ồ ể ộ ầ ườ ẳ ở ộ ố
O (còn đc g i là m t n a m t ph ng g c O) (h.6).ượ ọ ộ ử ặ ẳ ố
Trên hình (h.6) đi m O và ph n đng th ng bên trái O l p thành tia Ox.ể ầ ườ ẳ ậ
Đi m O và ph n đng th ng bên ph i O là tia Oy.ể ầ ườ ẳ ả
Hai tia chung m t g c và t o thành m t đng th ng là hai tia đi nhau. ộ ố ạ ộ ườ ẳ ố
M i đi m trên đng th ng là g c c a hai tia đi nhau.ỗ ể ườ ẳ ố ủ ố
6. Đo n th ngạ ẳ
Đo n th ng AB là hình g m hai đi m A,ạ ẳ ồ ể
B và t t c các đi m n m gi a A, B ấ ả ể ằ ữ
(h.7).
Khi hai đo n th ng ho c m t đo n th ng v i m t đng th ng ho c m tạ ẳ ặ ộ ạ ẳ ớ ộ ườ ẳ ặ ộ
đo n th ng v i m t tia ch có m t đi m chung, ta nói chúng c t nhau. ạ ẳ ớ ộ ỉ ộ ể ắ
Đ so sánh hai đo n th ng ta so sánh đ dài c a chúng. (h.8)ể ạ ẳ ộ ủ
Toán 6 – H c Kì I – Nguy n Văn Quy n – 0938.59.6698 – s u t m và biên so nọ ễ ề ư ầ ạ
Đo n th ng AB b ng đo n th ng CD: ạ ẳ ằ ạ ẳ
Đo n th ng EG l n h n đo n th ng CD: ạ ẳ ớ ơ ạ ẳ
Đo n th ng AB nh h n đo n th ng EG: ạ ẳ ỏ ơ ạ ẳ
N u đi m M n m gi a hai đi m A và B thì Ng c l i, n u thì đi m M ế ể ằ ữ ể ượ ạ ế ể
n m gi a hai đi m A và B (h.9).ằ ữ ể
7. Trung đi m c a đo n th ngể ủ ạ ẳ
Trung đi m M c a đo n th ng AB là đi m n m gi a A và B và cách đu ể ủ ạ ẳ ể ằ ữ ề
A, B (h.10).
B. Bài t pậ
D ng 1: V hình theo các di n đt sau.ạ ẽ ễ ạ
Bài 1:
a) V năm đi m M, N, P, Q, R sao cho ba đi m M, N, P th ng hàng, ba đi m ẽ ể ể ẳ ể
N, P, Q th ng hàng còn ba đi m N, P, R không th ng hàng. ẳ ể ẳ
b) K các đng th ng đi qua các c p đi m. Có bao nhiêu đng th ng? Kẻ ườ ẳ ặ ể ườ ẳ ể
tên các đng th ng đó.ườ ẳ
c) Có bao nhiêu đo n th ng? K tên các đo n th ng đó.ạ ẳ ể ạ ẳ
d) K tên các tia g c P. Trong các tia đó hai tia nào là hai tia đi nhau? Hai tiaể ố ố
trùng nhau?
Toán 6 – H c Kì I – Nguy n Văn Quy n – 0938.59.6698 – s u t m và biên so nọ ễ ề ư ầ ạ
Bài 2: Trên đng th ng d l y các đi m M, N, P, Q theo th t y và đi m A ườ ẳ ấ ể ứ ự ấ ể
không thu c đng th ng d.ộ ườ ẳ
a) V tia AM, tia QAẽ
b) V đo n th ng NA, đng th ng APẽ ạ ẳ ườ ẳ
c) Vi t tên hai tia đi nhau g c N, hai tia trùng nhau g c Nế ố ố ố
d) Có t t c m y đo n th ng trên hình v ? Hãy vi t tên các đo n th ng đó? ấ ả ấ ạ ẳ ẽ ế ạ ẳ
Bài 2: V b n đi m A, B, C, D trong đó không có ba đi m nào th ng hàng. V ẽ ố ể ể ẳ ẽ
đng th ng AC, tia DB, đo n th ng BC, đi m N n m gi a hai đi m B và C, ườ ẳ ạ ẳ ể ằ ữ ể
đi m K thu c tia DB sao cho K không n m gi a D và B.ể ộ ằ ữ
Bài 3: V ba đi m M, N, P không th ng hàng. V hai tia MN và MPPẽ ể ẳ ẽ
a) V tia Mx c t đng th ng NP t i H n m gi a N và Pẽ ắ ườ ẳ ạ ằ ữ
b) V tia My c t đng th ng NP t i K không n m gi a N và Pẽ ắ ườ ẳ ạ ằ ữ
c) V đng th ng a đi qua K và c t trung đi m I c a đo n th ng MN. ẽ ườ ẳ ắ ể ủ ạ ẳ
Bài 4:
a) V hai tia đi nhau Ox và Oy.ẽ ố
b) L y Vi t tên các tia trùng v i tia Ay. ấ ế ớ
c) Hai tia Ab và Oy có trùng nhau không? Vì sao?
d) Hai tia Ax và Ay có đi nhau không? Vì sao? ố
D ng 2: Tính đ dài đo n th ng; ch ng minh trung đi m c a đo n th ngạ ộ ạ ẳ ứ ể ủ ạ ẳ
Bài 1: Trên tia Ox, l y hai đi m A và B sao cho OA = 3cm, OB = 6cm.ấ ể
a) Đi m A có n m gi a O và B không? Vì sao? ể ằ ữ
b) Ch ng minh A là trung đi m c a đo n th ng OB.ứ ể ủ ạ ẳ
Bài 2: Trên cùng tia Ox, l y ấ
a) Trong ba đi m A, B, C đi m nào n m gi a hai đi m còn l i.ể ể ằ ữ ể ạ
b) Tính đ dài đo n BCộ ạ
c) L y đi m M sao cho B là trung đi m c a đo n th ng AM. Tính BM, AM, ấ ể ể ủ ạ ẳ
MC.
Bài 3: Trên tia Ox xác đnh hai đi m A và B sao cho OA = 7cm, OB = 3cm. ị ể
Toán 6 – H c Kì I – Nguy n Văn Quy n – 0938.59.6698 – s u t m và biên so nọ ễ ề ư ầ ạ
a) Tính AB. Đi m B có là trung đi m c a OA không? Vì sao? ể ể ủ
b) Trên tia đi c a tia Ox, l y đi m C sao cho OC = 3cm. Đi m O có là trungố ủ ấ ể ể
đi m c a BC không? Vì sao?ể ủ
Bài 4: Trên đo n th ng AB = 6cm. V đi m M sao cho AM = 2cm.ạ ẳ ẽ ể
a) Tính BM
b) L y C là trung đi m BM. Ch ng t M là trung đi m AC? ấ ể ứ ỏ ể
Bài 5: Cho đo n th ng AC = 5cm. Đi m B n m gi a A và C sao cho BC = 3cm. ạ ẳ ể ằ ữ
a) Tính đ dài đo n th ng AB.ộ ạ ẳ
b) Trên tia đi c a tia BA l y đi m D sao cho BD = 3AB. Đi m C có là trungố ủ ấ ể ể
đi m BD không? ể
Bài 6: Trên tia Ox l y hai đi m A và B sao cho OA = 2cm, OB = 4cm.ấ ể
a) Đi m A có là trung đi m c a đo n th ng OB không? Vì sao? ể ể ủ ạ ẳ
b) Trên tia đi c a tia Ox l y đi m C sao cho O là trung đi m c a AC. Tính ố ủ ấ ể ể ủ
AC, BC
c) Trên đo n OB l y D sao cho OB = 4OD. Tính BDạ ấ
d) Trên tia Ox l y E sao cho OE = 7cm. B có n m gi a D và E không? Vì ấ ằ ữ
sao?
Bài 7: Trên tia Oy xác đnh hai đi m M và N sao cho OM = 6cm, ON = 4cm.ị ể
a) Tính MN
b) Trên tia đi c a tia Oy xác đnh đi m P sao cho OP = 4cm. Đi m O có là ố ủ ị ể ể
trung đi m c a PN không? Vì sao? ể ủ
Bài 8: V đo n th ng và đi m C thu c AB sao cho ẽ ạ ẳ ể ộ
a) Tính đ dài các đo n AC, CB.ộ ạ
b) L y đi m M sao cho C là trung đi m c a đo n th ng BM. Ch ng minh ấ ể ể ủ ạ ẳ ứ
đi m M là trung đi m c a đo n th ng AC.ể ể ủ ạ ẳ
Bài 9: V đo n có đi m C n m gi a A và B sao cho Tính đ dài các đo n ẽ ạ ể ằ ữ ộ ạ
th ng AC và CB. ẳ
Bài 10: Trên tia Ax l y Đi m M n m gi a hai đi m A và B sao cho ấ ể ằ ữ ể
a) Tính AM và MB