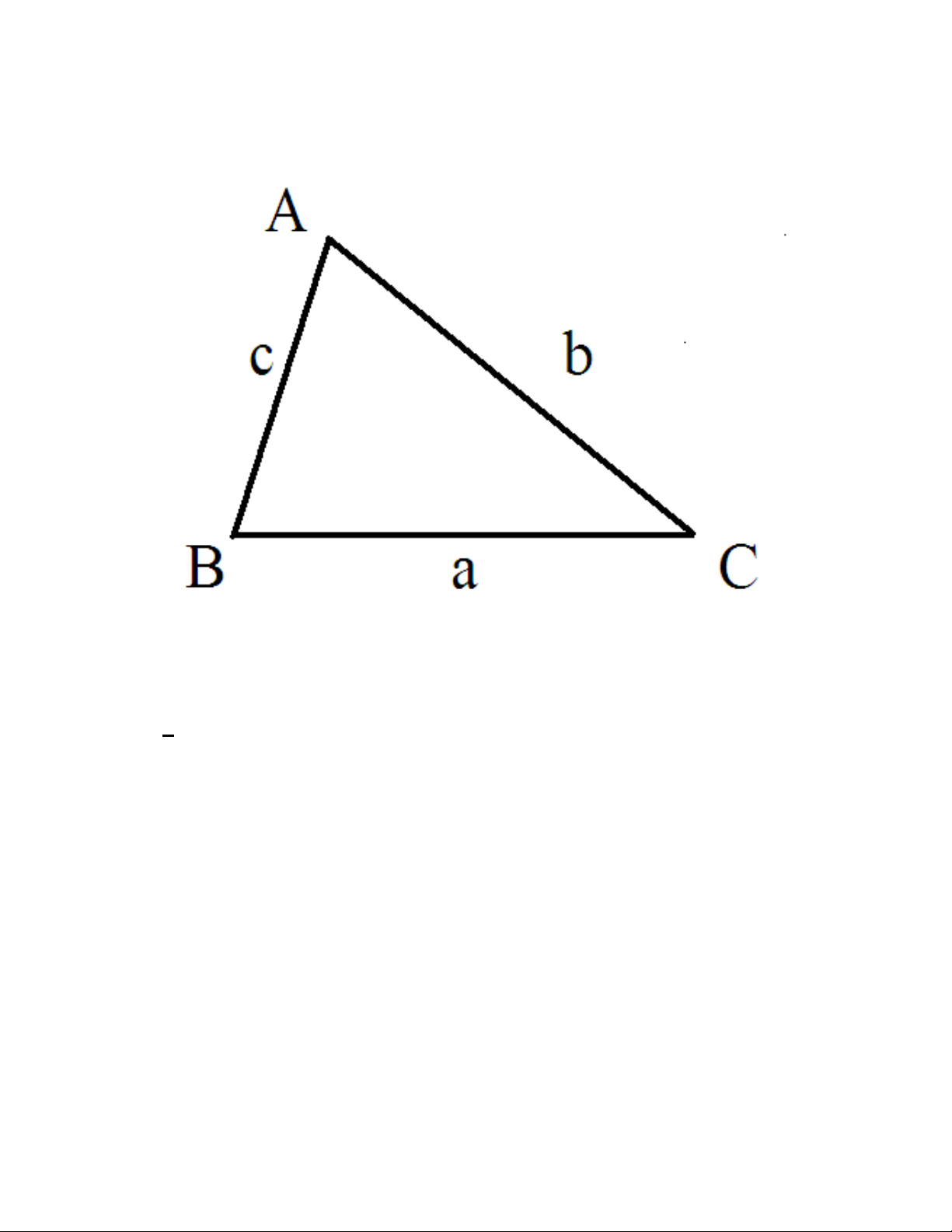
Trong tam giác
Chú thích:
r, r, R: bán kính đng tròn n i ti p, bàng ti p,ườ ộ ế ế
ngo i ti p tam giác ABCạ ế
A, B, C: góc A, B, C c a tam giác ABCủ
a, b, c: c nh BC, AC, AB c a tam giác ABCạ ủ
p: n a chi vi tam giác ABCử
Đnh lý hàm s Cos: ị ố
a→2 = b2 + c2 – 2bcCosA
a = bCosC ± →
TanA = →

Trong t di n có Sứ ệ 1, S2, S3, S4 là di n tích 4 m t,ệ ặ
S1S2 là góc nh di n:ị ệ
S12 = S22 + S32 + S42 – 2 (S2S3.Cos S2S3 + S3S4.Cos S3S4
+ S2S4.Cos S2S4)
Đnh lý hàm s Sin:ị ố
= = = 2R→
=
=
Đnh lý hàm s Tan:ị ố
= →
= →
Tan= Tan- Cot→
Đnh lý hàm s Cot:ị ố
= = →
Cot= →
Cot= →
Cot= →
Công th c Mollweide:ứ
= →
= →
Tam giác:
S = aha
= pr
=
= bcSinA
2

=
=
=
=
= p2TanTanTan
= 2R2.SinA.SinB.SinC
= (a2Sin2B + b2Sin2A)
= Rr(sinA + SinB + SinC)
= p(p – a).Tan
=
= ra.(p – a)
ma =
=
la =
=
=
r = =
c = a.CosB + b.CosA
Tam giác cân có 2 c nh bên là a, c nh đáy là c:ạ ạ
c2 = 2a2(1 – CosC)
Tam giác vuông có c nh huy n là c:ạ ề
S = (p – a)(p – b)
r = =
Tam giác có A > 90o; a < b; a < bSinA thì:
B = arcsin
3

Ho c B = 180ặo - arcsin
L ng giác:ượ
Chú thích:
A, B: góc b t kìấ
Cos2A + Sin2A = 1
SinA + SinB = 2Sin.Cos
SinA - SinB = 2Sin.Cos
Tan=
Tan =
Tan=
=
=
Tan(+45o) = TanA +
=
H ng đng th c đáng nh :ằ ẳ ứ ớ
Chú thích:
a, b, c: các s th c b t kìố ự ấ
(a + b + c)→3
= a3 + b3 + c3 + 3(a + b)(b + c)(a + c)
a→3 + b3 + c3 – 3abc
= (a + b + c)(a2 + b2 + c2 – ab – bc – ac)
Gi i ph ng trình b c 2:ả ươ ậ
ax2 + bx + c = 0
x =
x =
4

x1 + x2 = ; x1x2 =
N u a + b + c = 0 thì xế1 = 1; x2 =
N u a – b + c = 0 thì xế1 = -1; x2 = -
N u ac < 0 thì có hai nghi m phân bi t.ế ệ ệ
Gi i ph ng trình b c 3:ả ươ ậ
Ph ng pháp t ng quát:ươ ổ
ax3 + bx2 + cx + d = 0
Đt các giá tr :ặ ị
∆ = b2 – 3ac
k =
1) N uế ∆ > 0 thì
TH1: |k| ≤ 1: Ph ng trình có ba nghi mươ ệ :
x1 =
x2 =
x3 =
TH2: |k| > 1: Ph ng trình có m t nghi mươ ộ ệ duy
nh t:ấ
x = .() -
2) N uế ∆ = 0: Ph ng trình có m t nghi m b iươ ộ ệ ộ
x =
3) N uế ∆ < 0: Ph ng trình có m t nghi m duy nh tươ ộ ệ ấ :
x = .() -
5
















