BỘ GIÁO DỤC VÀ ĐÀO TẠO
⎯⎯⎯⎯⎯⎯⎯⎯
ĐỀ CHÍNH THỨC
ĐÁP ÁN – THANG ĐIỂM
ĐỀ THI TUYỂN SINH ĐẠI HỌC NĂM 2009
Môn thi: TOÁN; Khối: B
(Đáp án - thang điểm gồm 04 trang)
ĐÁP ÁN − THANG ĐIỂM
Câu Đáp án Điểm
1. (1,0 điểm) Khảo sát…
• Tập xác định:
.D=\
• Sự biến thiên:
- Chiều biến thiên: hoặc
3
'8 8;yxx=− '0y=⇔0x=1.x=±
Hàm số nghịch biến trên: và đồng biến trên: và (1
(;1)−∞ − (0;1); (1;0)−; ).+∞
0,25
- Cực trị: Hàm số đạt cực tiểu tại đạt cực đại tại y
1, 2;
CT
xy=± =− 0,x=CĐ
0.=
- Giới hạn:
lim lim .
xx
yy
→−∞ →+∞
==+∞ 0,25
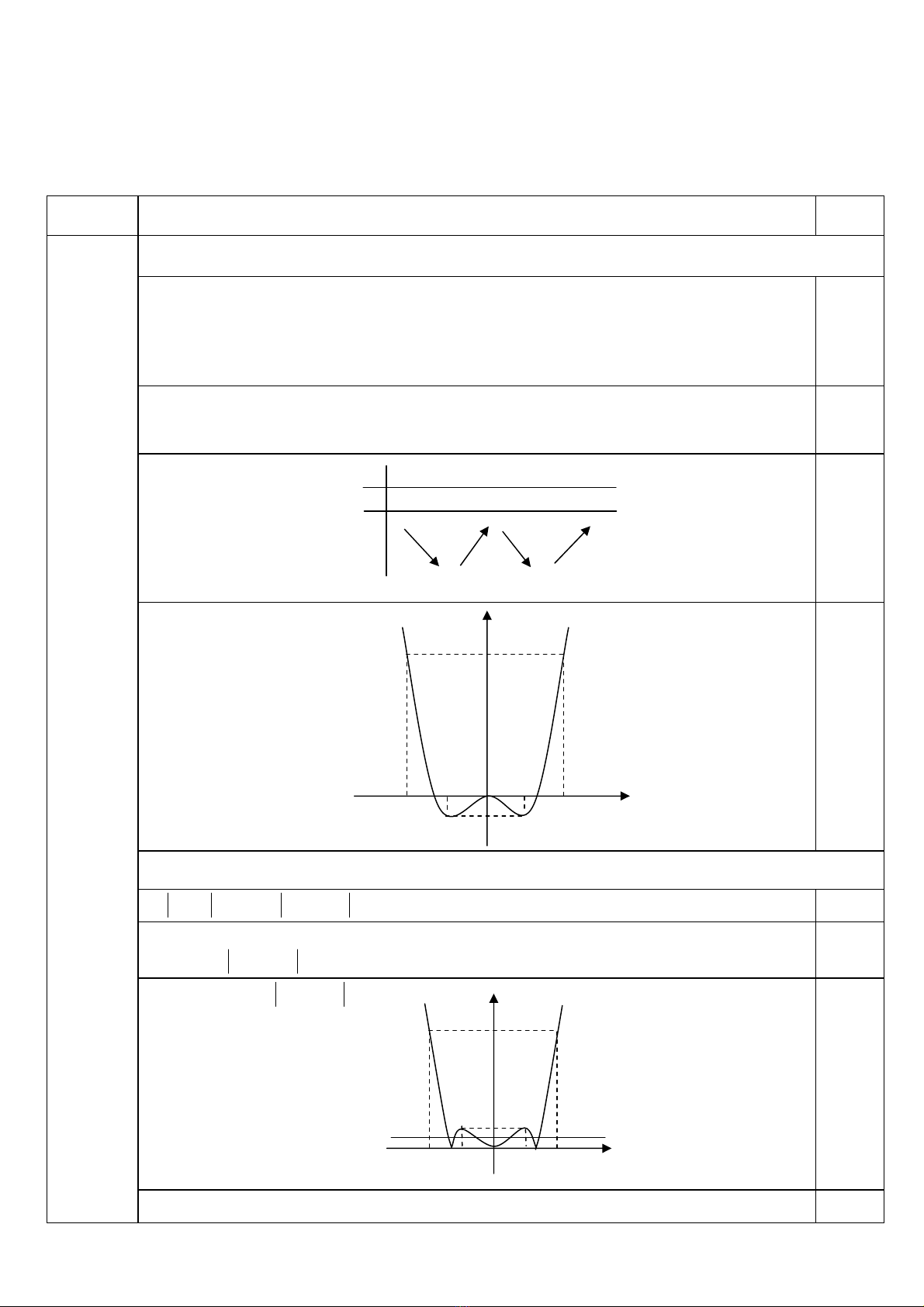
- Bảng biến thiên:
Trang 1/4
0,25
• Đồ thị:
0,25
2. (1,0 điểm) Tìm
...m
22 2
x
xm−=
⇔42
24 2.
x
xm−=
0,25
Phương trình có đúng nghiệm thực phân biệt khi và chỉ khi đường thẳng cắt đồ thị
hàm số
62ym=
42
24
y
xx=− tại điểm phân biệt.
60,25
Đồ thị hàm số 42
24
y
xx=−
và đường thẳng .
2ym=
0,25
I
(2,0 điểm)
Dựa vào đồ thị, yêu cầu bài toán được thoả mãn khi và chỉ khi: 02 2m<<
⇔01m<<
x
−∞
1
−
01
+
∞
+
+∞
x
y' − 0 + 0 − 0
y
+∞
2−2−
0
O
y
2−
2−
1−1
16
2
y
O
x
2
2
1
−1
16
2
−
2ym=
.0,25

Trang 2/4
Câu Đáp án Điểm
1. (1,0 điểm) Giải phương trình…
Phương trình đã cho tương đương: 2
(1 2sin )sin cos sin 2 3 cos3 2cos 4
x
xxx x−++=
II
x
⇔ sin cos 2 cos sin 2 3 cos3 2cos 4
x
xxx x++=x 0,25
⇔ sin 3 3 cos3 2cos 4
x
xx+= ⇔cos 3 cos4 .
6
x
x
π
⎛⎞
−=
⎜⎟
⎝⎠ 0,25
⇔ 43 2
6
x
xk
ππ
=−+ hoặc 43 2
6
xx k
ππ
=− + + .
0,25
Vậy: 2
6
x
k
ππ
=− + hoặc 2()
42 7
xkk
ππ
=+ ∈].
0,25
2. (1,0 điểm) Giải hệ phương trình…
Hệ đã cho tương đương:
2
2
17
113
x
xyy
x
xyy
⎧++=
⎪
⎪
⎨
⎪++ =
⎪
⎩
(do không thoả mãn hệ đã cho)
0y=0,25
⇔ 2
17
113
x
xyy
x
xyy
⎧⎛⎞
++=
⎪⎜⎟
⎝⎠
⎪
⎨⎛⎞
⎪+−=
⎜⎟
⎪⎝⎠
⎩
⇔
2
11
20 0
1
7
xx
yy
xx
yy
⎧⎛⎞⎛⎞
⎪+++−=
⎜⎟⎜⎟
⎪⎝⎠⎝⎠
⎨⎛⎞
⎪=− +
⎜⎟
⎪⎝⎠
⎩
0,25
⇔
15
12
xy
x
y
⎧+=−
⎪
⎨
⎪=
⎩
(I) hoặc
14
3
xy
x
y
⎧+=
⎪
⎨
⎪=
⎩
(II). 0,25
(2,0 điểm)
(I) vô nghiệm; (II) có nghiệm: 1
(; ) 1;
3
xy ⎛⎞
=⎜⎟
⎝⎠
và
(; ) (3;1).xy =
Vậy: 1
(; hoặc (; ) 1;
3
xy ⎛⎞
=⎜⎟
⎝⎠ ) (3;1).xy =
0,25
Tính tích phân…
3ln,ux=+ 2;
(1)
dx
dv x
=+ 1,du dx
x
= 1.
1
vx
=− + 0,25
I
33
11
3ln
1(
1)
x
dx
xxx
+
=− +
++
∫0,25
33
11
3ln3 3 1
42
dx
dx 1
x
x
+
=− + + − +
∫∫
0,25
III
(1,0 điểm)
33
11
3ln3 1 27
ln ln 1 3 ln .
44
xx
−⎛⎞
=+−+=+
⎜⎟
⎝⎠
16
0,25
Tính thể tích khối chóp…
Gọi
D
là trung điểm và là trọng tâm tam giác
AC GABC
ta có '( )
B
G ABC⊥⇒
n
'
B
BG =60D
⇒
n
3
''.sin' 2
a
BG BB BBG==
và 2
a
BG = ⇒ 3.
4
a
BD =
Tam giác có:
ABC 3,
22
A
BAB
BC AC==
⇒.
4
AB
CD =
0,50
IV
(1,0 điểm)
222
B
A
B
CCDBD+= ⇒
222
6
39
4161
A
BAB a
+=
⇒ 313
,
13
a
AB = 313
;
26
a
AC =
2
93
.
104
ABC
a
SΔ= 0,25
'
B
C
'
G
C
'
A
D

Trang 3/4
Câu Đáp án Điểm
Thể tích khối tứ diện
':AABC ''
1'.
3
A ABC B ABC ABC
VV BGS
Δ
==
3
9.
208
a
= 0,25
Tìm giá trị nhỏ nhất của biểu thức…
Kết hợp với
3
()4xy xy++ ≥22
()4
x
yx+≥y suy ra: ⇒
32
()()2xy xy+++≥ 1.xy+≥ 0,25
A4422 22
3( ) 2( ) 1xyxy xy=++ −++
=
()
2
22 44 22
33
()2()
22
xy xy xy++ +−++1
0,25
≥
()()
22
22 22 22
332( ) 1
24
xy xy xy++ +−++
⇒
()()
2
22 22
921
4
Axy xy≥+−++.
Đặt , ta có
2
tx y=+
22
22
()1
22
xy
xy +
+≥ ≥
⇒ 1;
2
t≥ do đó 2
921
4
At t≥−+
.
Xét 2
9
() 2 1;
4
ft t t=−+
9
'( ) 2 0
2
ft t=−>
với mọi 1
2
t≥
⇒1;
2
19
min ( ) .
216
ft f
⎡⎞
+∞ ⎟
⎢
⎣⎠
⎛⎞
==
⎜⎟
⎝⎠ 0,25
V
(1,0 điểm)
9;
16
A≥ đẳng thức xảy ra khi 1.
2
xy== Vậy, giá trị nhỏ nhất của bằng A9.
16 0,25
1. (1,0 điểm) Xác định toạ độ tâm
...K
Gọi ⇔
(;);Kab ()KC∈22
4
(2) 5
ab−+=
(1); tiếp xúc
1
()C1,Δ2
Δ⇔
VI.a
7
252
ab a b−−
= (2). 0,25
(1) và (2), cho ta:
22
5( 2) 5 4
57
ab
ab a b
⎧−+ =
⎪
⎨−=−
⎪
⎩
(I) hoặc (II).
⇔
22
5( 2) 5 4
5( ) 7
ab
ab a b
⎧−+ =
⎨−=−
⎩
22
5( 2) 5 4
5( ) 7
ab
ab ba
⎧−+ =
⎨−= −
⎩0,25
(2,0 điểm)
(I) vô nghiệm; (II)
⇔
2
25 20 16 0
2
aa
ba
⎧−+=
⎨=−
⎩⇔2
284
(;) ; .
55
25 40 16 0
ab ab
bb
=
⎧⎛⎞
⇔=
⎨⎜⎟
−+= ⎝⎠
⎩ 0,25
Bán kính
1
():C22
.
5
2
ab
R−
==
Vậy: 84
;
55
K⎛⎞
⎜⎟
⎝⎠
và 22
.
5
R= 0,25
2. (1,0 điểm) Viết phương trình mặt phẳng ()...
P
Mặt phẳng ()
P
thoả mãn yêu cầu bài toán trong hai trường hợp sau:
Trường hợp 1: ()
P
qua ,
A
B và song song với
.CD 0,25
Vectơ pháp tuyến của ()
:P,.nABCD
⎡⎤
=⎣⎦
GJJJGJJJG
(3;1;2),AB =− −
JJJGJJJG
(2;4;0)CD =− ⇒(8;4;14).n=− − −
G
Phương trình ()
P
:
427150.xyz++−= 0,25
Trường hợp 2: ()
P
qua ,
A
B và cắt Suy ra
.CD ()
P
cắt CD tại trung điểm của
vectơ pháp tuyến của
I.CD
(1;1;1) (0; 1; 0);IAI⇒=−
JJG ():
P
, (2;0;3).nA=BAI
⎡⎤
=
⎣⎦
G
JJJGJJG 0,25
Phương trình
():2 3 5 0.Pxz+−=
Vậy () hoặc :4 2 7 15 0Pxyz++−= ():2 3 5 0.Pxz+−= 0,25
Tìm số phức
...z
Gọi
;zxyi=+ (2 ) ( 2) ( 1) ;zix yi
VII.a
22
(2 ) 10 ( 2) ( 1) 10zi x y−+= ⇔− +− =
−+=−+− (1). 0,25
22
.25 25zz x y=⇔+=
(2). 0,25
(1,0 điểm)
Giải hệ (1) và (2) ta được: hoặc (; Vậy: hoặc
(; ) (3;4)xy =) (5;0).xy =34zi=+ 5.z=0,50

Trang 4/4
Câu Đáp án Điểm
1. (1,0 điểm) Xác định toạ độ các điểm ,...
B
C
Gọi là hình chiếu của trên suy ra là trung điểm H A ,ΔH.
B
C
9
(, ) ;
2
AH d A BC==
242.
ABC
S
BC AH
Δ
==
VI.b
2
297.
42
BC
AB AC AH== + =
0,25
Toạ độ
B
và C là nghiệm của hệ:
()( )
22
97
14
2
40.
xy
xy
⎧++− =
⎪
⎨
⎪−−=
⎩
0,25
Giải hệ ta được: 11 3
(; ) ;
22
xy ⎛
=⎜
⎝⎠
⎞
⎟
hoặc 35
(; ) ; .
22
xy ⎛⎞
=−
⎜⎟
⎝⎠
0,25
Vậy 11 3 3 5
;, ;
22 2 2
BC
⎛⎞⎛
−
⎜⎟⎜
⎝⎠⎝
⎞
⎟
⎠
hoặc 35 113
;, ;
22 22
BC
⎛⎞⎛
−
⎜⎟⎜
⎝⎠⎝.
⎞
⎟
⎠
0,25
2. (1,0 điểm) Viết phương trình đường thẳng…
Gọi là đường thẳng cần tìm; nằm trong mặt phẳng
qua và song song với
Δ Δ
()QA().
P
Phương trình () : 2 2 1 0.Qx y z−++=
0,25
,K là hình chiếu của H
B
trên Ta có
,Δ().Q
B
KBH≥ nên là đường thẳng cần tìm. AH 0,25
Toạ độ thoả mãn:
(;;)Hxyz=
113
122
2210
xyz
xyz
−+−
⎧==
⎪−
⎨
⎪−++=
⎩
⇒
1117
;; .
999
H⎛⎞
=−
⎜⎟
⎝⎠
0,25
(2,0 điểm)
26 11 2
;; .
99 9
AH ⎛
=−
⎜
⎝⎠
JJJG
H
B
C
A
Δ
B
⎞
⎟
Vậy, phương trình 31
:.
26 11 2
xyz+−
Δ==
− 0,25
Tìm các giá trị của tham số
...m
Toạ độ ,
A
B thoả mãn:
21x
x
m
x
yxm
⎧−=− +
⎪
⎨
⎪=− +
⎩
⇔
2
210,(0)
.
xmx x
yxm
⎧−−= ≠
⎨=− +
⎩
(1)
0,25
Nhận thấy (1) có hai nghiệm thực phân biệt 12
,
x
x khác 0 với mọi
.m
Gọi ta có: .
11 2 2
(; ), (; )Ax y Bx y 22 2 2
12 12 12
()( )2()
A
Bxx yy xx=− +− = − 0,25
Áp dụng định lí Viet đối với (1), ta được:
2
22
12 12
2( ) 4 4.
2
m
AB x x x x
⎡⎤
=+− =+
⎣⎦
0,25
VII.b
(1,0 điểm)
2
4416 2
2
m
AB m=⇔ += ⇔ =± 6.
0,25
-------------Hết-------------
Q
K
A
H
















