Trường THCS Lê Quang Cường Đề cương giữa HK2 (23-24)
Trang 1
ĐỀ CƯƠNG ÔN TẬP KIỂM TRA GIỮA HỌC KỲ II
NĂM HỌC: 2023 – 2024
TOÁN 8
A. TÓM TẮT NỘI DUNG KIẾN THỨC
I. XÁC SUẤT - ĐẠI SỐ
Chương 9. Một số yếu tố xác suất
- Trong một phép thử, mỗi kết quả là một biến cố xảy ra được gọi là một kết quả thuận lợi cho biến
cố đó.
- Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản.
P(A)=Số các kết quả thuận lợi cho A
Tổng số các kết quả có thể xảy ra
- Xác suất thực nghiệm của một biến cố trong một số trò chơi đơn giản là:
()mA
m
với m(A) là số lần
xuất hiện biến cố A khi thực hiện một phép thử m lần.
Chương 5: Hàm số và đồ thị
II. HÌNH HỌC
Chương 7: Định lí Thalès
- Định lí Thalès và ứng dụng trong tam giác.
Tỉ số của hai đoạn thẳng AB và CD được ký hiệu là
AB
CD
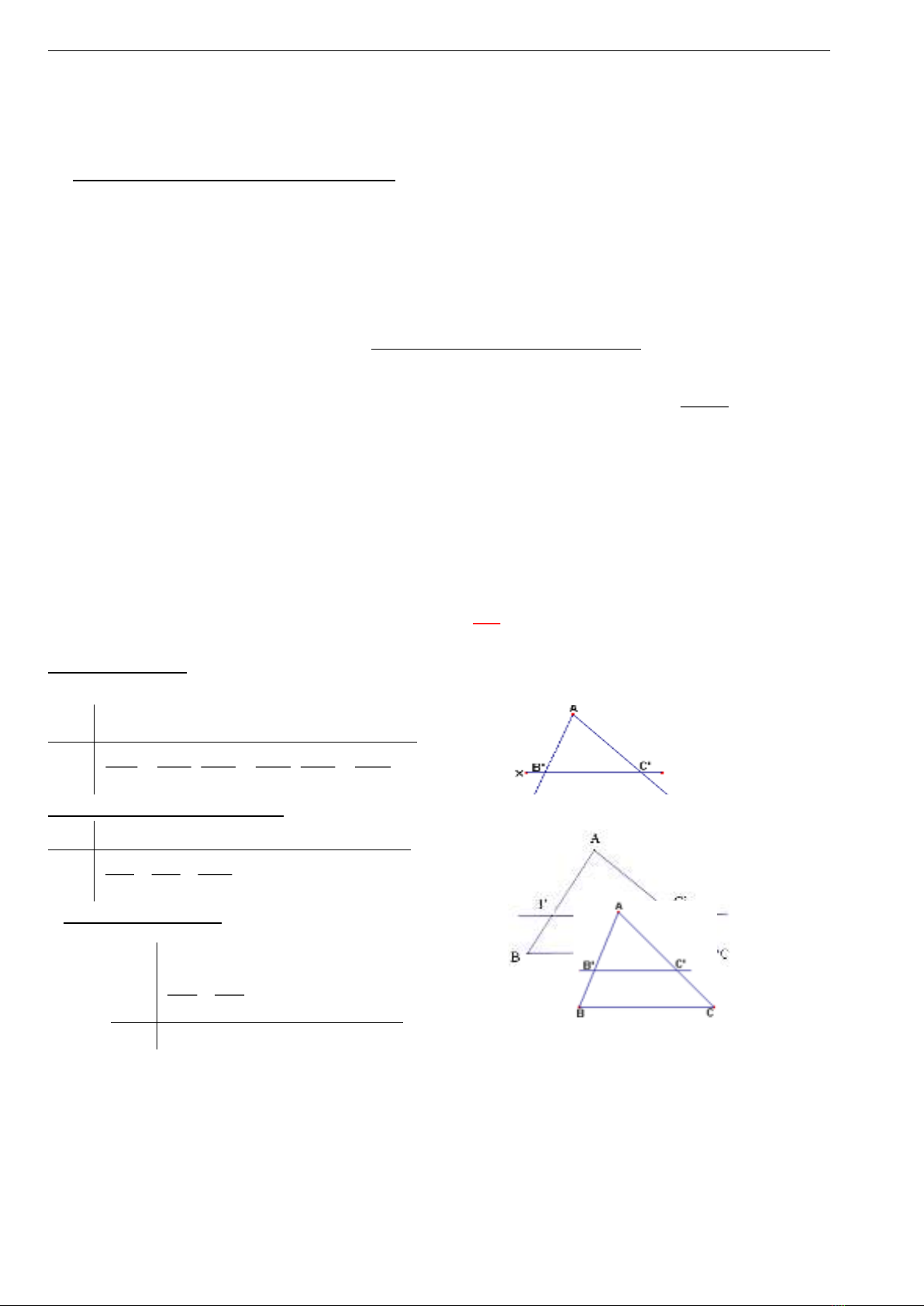
* Định lý Thalès.
GT
ABC, B’C’//BC
( )
' , 'B AB C AC
KL
' ' ' ' ' '
,,
''
= = =
AB AC AB AC B B C C
AB AC B B A C AB AC
* Hệ quả của định lý Thalès.
GT
KL
AB' AC' B'C'
AB AC BC
==
* Định lý Thalès đảo.
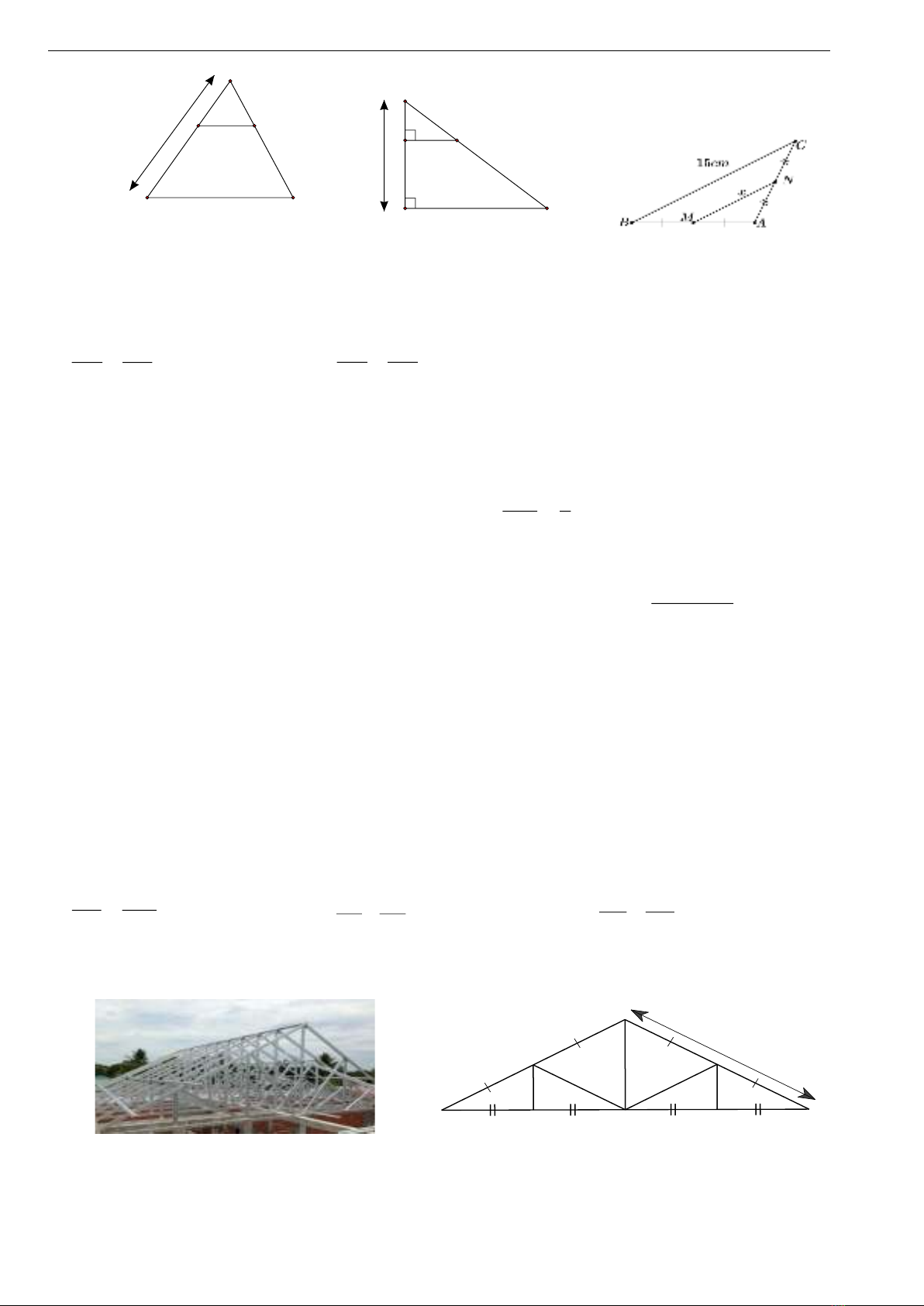
- Đường trung bình của tam giác.
Chú ý: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua
trung điểm của cạnh thứ ba.
Định nghĩa: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
Tính chất: Đường trung bình của tam giác thì song song với cạnh thứ 3 và bằng nửa cạnh ấy.
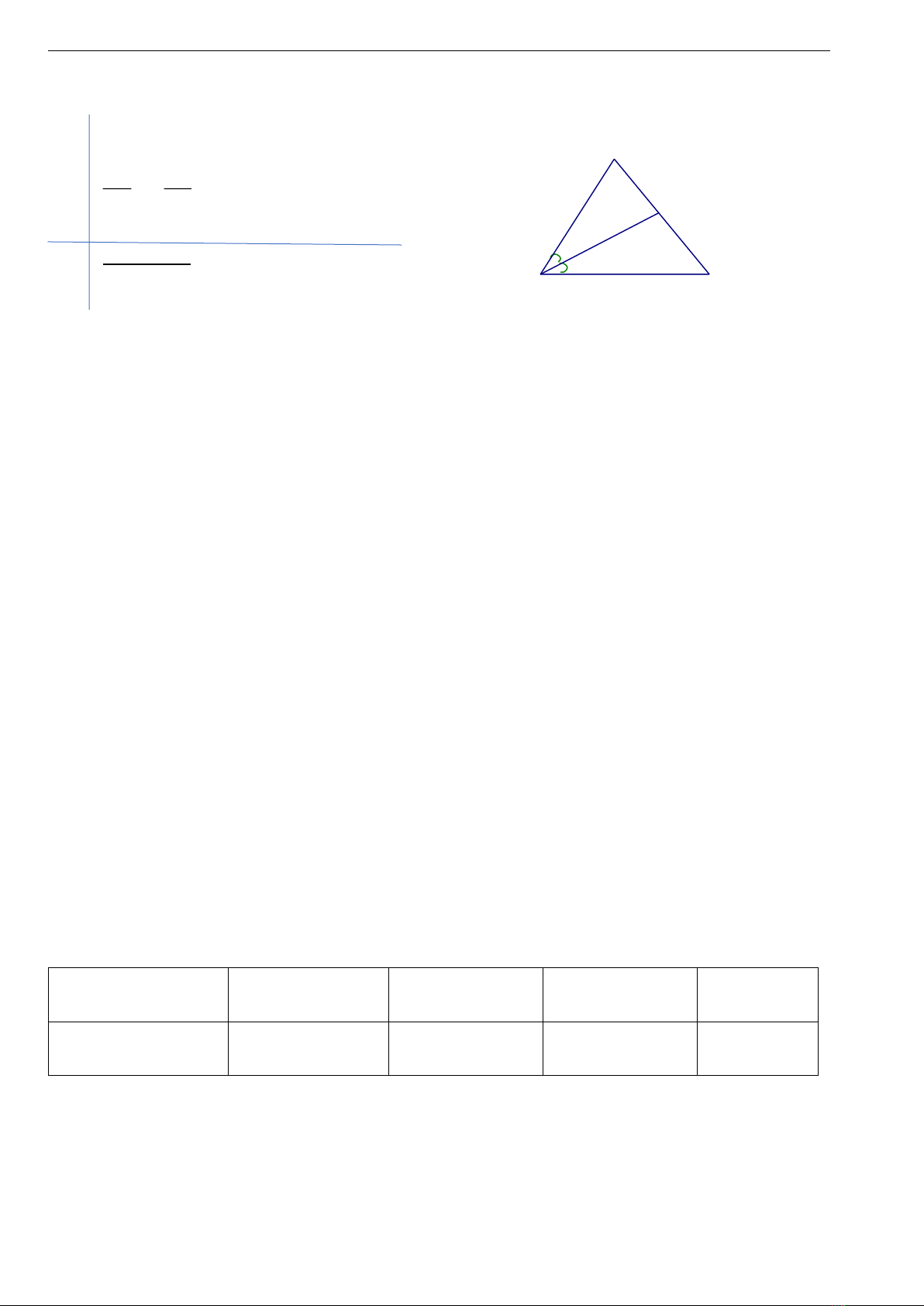
- Tính chất đường phân giác của tam giác.
GT
ABC, B’AB, C’AC
AB' AC'
B'B C'C
=
KL
B’C’//BC
Trường THCS Lê Quang Cường Đề cương giữa HK2 (23-24)
Trang 2
Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ vớ hai cạnh
kề hai cạnh ấy
GT
ABC, AD là tia phân giác
BAC
( D
BC )
KL
DB
DC
=
AB
AC
B. BÀI TẬP:
Xem lại các bài tập trong sách giáo khoa
Dạng 1. Các bài toán về xác suất
Bài 1. Một túi đựng 10 tấm thẻ bài có kích thước giống nhau và được ghi số
1; 2; 3; ...; 10.
Hoa rút ngẫu
nhiên một tấm thẻ từ trong hộp.
a) Liệt kê các kết quả có thể của hành động trên.
b) Liệt kê các kết quả thuận lợi cho các biến cố:
A: “Rút được tấm thẻ có ghi số lẻ”;
B: “Rút được tấm thẻ có ghi số nguyên tố”;
C: “Rút được tấm thẻ có ghi số chia hết cho 3”.
Bài 2. Một túi đựng bút tô màu của bé Mai có 5 chiếc bút màu vàng, 3 chiếc bút màu cam, 4 chiếc bút
màu xanh và 2 chiếc bút màu tím (các chiếc bút có cùng khối lượng và kích thước). Bé Mai lấy ngẫu
nhiên một chiếc bút từ trong túi. Tính xác suất của các biến cố sau:
A: “Lấy được chiếc bút màu tím”;
B: “Lấy được chiếc bút màu cam hoặc màu xanh”;
C: “Không lấy được chiếc bút màu vàng”;
D: “Lấy được chiếc bút màu vàng”.
Bài 3. Một hộp có 8 quả bóng có cùng kích thước và khối lượng, được đánh số 5; 7; 9; 10; 12; 14; 19;
25. Chọn ngẫu nhiên một quả bóng từ hộp. Hãy nêu các kết quả thuận lợi cho các biến cố sau:
a) A: “Số ghi trên quả bóng lấy ra là số có hai chữ số:
b) B: “Số ghi trên quả bóng lấy ra là số chính phương”
Bài 4. Trong một chiếc hộp có 15 tấm thẻ giống nhau được đánh số 10; 11; ... ; 24. Rút ngẫu nhiên một
tấm thẻ từ trong hộp. Tính xác suất của các biến cố sau:
a) A: "Rút được tấm thẻ ghi số lẻ"
b) B: "Rút được tấm thẻ ghi số nguyên tố"
Bài 5. Thống kê thời gian của 78 chương trình quảng cáo trên Đài truyền hình tỉnh X cho kết quả như
sau:
Thời gian quảng cáo
trong khoảng
Từ 0 đến 19 giây
Từ 20 đến 39
giây
Từ 40 đến 59
giây
Trên 60 giây
Số chương trình
quảng cáo
17
38
19
4
Tính xác suất thực nghiệm của các biến cố sau:
a) E: "Chương trình quảng cáo của Đài truyền hình tỉnh X kéo dài từ 20 đến 39 giây"
b) F: "Chương trình quảng cáo của Đài truyền hình tỉnh X kéo dài trên 1 phút"
c) G:" Chương trình quảng cáo của Đài truyền hình tỉnh X kéo dài trong khoảng từ 20 đến 59 giây"
Dạng 2. Các bài tập về hàm số và đồ thị.
D
D
C
A
Trường THCS Lê Quang Cường Đề cương giữa HK2 (23-24)
Trang 3
Bài 1: Cho hàm số
( ) 5 3y f x x= = − +
. Hãy tính
(0)f
,
( 1)f−
,
1
2
f


.
Bài 2: Cho hàm số
2
( ) 2 1y f x x= = −
.
a) Tính
(1)f
,
1
4
f
−


,
( 3)f−
,
(10)f
.
b) Lập bảng các giá trị tương ứng của y khi x lần lượt nhận các giá trị:
-2; -1; 0; 1; 2
Bài 3: Một xe ô tô chạy với tốc độ 50 km/h trong thời gian t (h).
a) Viết hàm số biểu thị quãng đường
()St
(km) mà ô tô đi được trong thời gian
t
(h).
b) Tính quãng đường
()St
(km) mà ô tô đi được trong thời gian
2t=
(h);
3t=
(h).
Bài 4: Vẽ một hệ trục tọa độ Oxy và đánh dấu các điểm
(2; 3)A−
,
( 1;4)B−
,
( 3;0)C−
.
Bài 5: Cho mặt phẳng tọa độ Oxy như hình bên. Hãy xác định tọa độ các điểm A, B, C, D, O.
Bài 6: Vẽ đồ thị của hàm số
()y f x=
cho bằng bảng sau:
x
-1
0
1
2
3
y=f(x)
-3
-1
1
3
5
Bài 7: Tìm các hàm số bậc nhất trong các hàm số sau đây và xác định các hệ số a, b của chúng.
a)
12yx=−
b)
210yx=+
c)
35yx=+
d)
1
3
yx=−
Bài 8: Với giá trị nào của m thì mỗi hàm số sau đây là hàm số bậc nhất?
a)
31y mx=+
b)
( 5) 2y m x= − +
c)
4y m x=−
d)
4( 1)y m m x= − +
Bài 9: Vẽ đồ thị của các hàm số sau:
a)
2yx=
b)
1
2
yx=−
c)
4yx
=+
d)
23yx= − +
Bài 10: a) Vẽ đồ thị các hàm số sau đây trên cùng một mặt phẳng tọa độ:
2yx=
;
21yx=+
;
2yx=−
;
21yx= − +
b) Bốn đồ thị nói trên cắt nhau tại các điểm A, B, C, D. Tứ giác có 4 đỉnh A, B, C, D là hình gì? Giải
thích?
Dạng 3. Hình học
Bài 1. Tìm độ dài
, xy
trong mỗi trường hợp sau:
Trường THCS Lê Quang Cường Đề cương giữa HK2 (23-24)
Trang 4
Hình 1
Hình 2
Hình 3
Bài 2. Cho
ABC
trung tuyến
.AD
Vẽ tia phân giác của
ADB
cắt
AB
tại
,M
tia phân giác của
ADC
cắt
AC
tại
.N
Chứng minh rằng:
a)
.
MB BD
MA AD
=
b)
.
MB NC
MA NA
=
c)
// .MN BC
Bài 3. Cho tam giác
ABC
vuông tại
( )
.A AB AC
Gọi
I
là trung điểm của cạnh
.BC
Qua
I
vẽ
IN
vuông góc với
AC
tại
.N
Lấy điểm
D
sao cho
N
là trung điểm của
.ID
a) Chứng minh
N
là trung điểm của AC.
b) Đường thẳng
BN
cắt cạnh
DC
tại
.K
Chứng minh
1.
3
DK
DC =
Bài 4. Cho tứ giác
.ABCD
Gọi
, , E F I
theo thứ tự là trung điểm của
, , .AD BC AC
Chứng minh rằng: a)
//EI CD
và
// .IF AB
b)
.
2
AB CD
EF +
Bài 5. Cho hình thang
ABCD
có hai đáy
AB
và
.CD
Gọi
M
là trung điểm của
,CD
E
là giao điểm
của
MA
và
,BD
F
là giao điểm của
MB
và
.AC
a) Chứng minh rằng
// .EF AB
b) Đường thẳng
EF
cắt
,AD BC
lần lượt tại
H
và
.N
Chứng minh
.HE EF FN==
c) Biết
7,5 cm, 12 cm.AB CD==
Tính độ dài
.HN
Bài 6. Cho
ABC
có
AD
là trung tuyến, trọng tâm
,G
đường thẳng đi qua
G
cắt các cạnh
,AB AC
lần lượt tại
,.EF
Từ
,BC
kẻ các đường song song với
EF
cắt
AD
lần lượt tại
,.MN
Chứng minh
rằng:
a)
.
BE MG
AE AG
=
b)
1.
BE CF
AE AF
+=
c)
3.
AB AC
AE AF
+=
Bài 7: Vì kèo mái tôn là một trong những bộ phận không thể thiếu trong cấu tạo mái nhà lợp tôn. Nó
giúp chống đỡ và giảm trọng lực của những ảnh hưởng từ các yếu tố bên ngoài tác động vào (Hình a).
Hình a
Hình b
Một vì kèo mái tôn được vẽ lại như Hình b. Tính độ dài
x
của cây chống đứng bên và độ dài
y
của
cánh kèo.
MN // AB
7
2
6
x
N
B
C
A
M
3
15
5
y
F
N
P
M
E
y
x
2,7 m
2,8 m
Trường THCS Lê Quang Cường Đề cương giữa HK2 (23-24)
Trang 5
Bài 8. Lúc 6 giờ sáng, bạn Hải đi xe đạp từ điểm
A
đến trường (tại điểm
)B
phải leo lên và xuống một
con dốc với đỉnh dốc tại điểm
C
(như hình vẽ).
Điểm
H
là một điểm thuộc đoạn thẳng
AB
sao cho
CH
đường là phân giác
,ACB
0,32 kmAH =
và
0,4 km.BH =
Biết bạn Hải đi xe đạp đến
C
lúc 6 giờ 30 phút với tốc độ trung bình lên dốc là 4
km/h. Hỏi bạn Hải đến trường lúc mấy giờ nếu tốc độ trung bình xuống dốc là 10 km/h?
C. MỘT SỐ ĐỀ THAM KHẢO
ĐỀ 1
Bài 1 (2,0 điểm):
Hình bên mô tả một đĩa tròn bằng bìa cứng được chia làm tám phần bằng
nhau và ghi các số 1; 2; 3; 4; 5; 6; 7; 8. Chiếc kim được gắn cố định vào trục
quay ở tâm của đĩa. Quay đĩa tròn một lần.
Hãy nêu các kết quả thuận lợi và tính xác suất cho các biến cố sau:
a) A: “Mũi tên chỉ vào hình quạt ghi số lớn hơn 5”;
b) B: “Mũi tên chỉ vào hình quạt ghi số nhỏ hơn 6”
Bài 2 (1,5 điểm): Một công ty chế biến hạt điều đã thống kê các loại hạt điều
thu hoạch được như bảng sau:
Loại hạt điều
Loại 1
Loại 2
Loại 3
Khối lượng thu hoạch được
1 450
2 230
1860
a) Hãy tính xác suất thực nghiệm của biến cố sau (làm tròn kết quả đến chữ số thập phân thứ tư):
A: “Hạt điều đạt loại 2 và loại 3”.
b) Công ty lấy ngẫu nhiêm 100 kg hạt điều chưa phân loại và tiến hành phân loại. Em hãy dự đoán xem
có bao nhiêu kilôgam hạt điều loại 1?
Bài 3 (1,0 điểm). Hàm số
( )
y f x=
được xác định bởi công thức
( )
35y f x x= = +
.
Tính các giá trị sau:
( )
25 ;9
81
ff
 −


.
Bài 4 (2,0 điểm). Cho hàm số
y x 1=+
có đồ thị là
( )
d
và hàm số
y x 3= − +
có đồ thị là (d').
a. Vẽ (d) và (d') trên cùng một mặt phẳng tọa độ.
b. Hai đường thẳng
( )
d
và
( )
d
cắt nhau tại
C
. Tìm tọa độ điểm
C
Bài 5 (3,0 điểm) Cho ΔABC vuông tại A có AB = 8cm, AC = 6cm. Trên cạnh AB lấy điểm D sao cho
AD = 4cm, từ D kẻ DE song song với cạnh AC (E thuộc BC)
a) Tính các tỉ số
AD
AB
, rồi suy ra tỉ số
CE
BC
b) Tính DE?
c) Đường phân giác của
BAC
cắt BC tại I. Tính IB, IC?
Bài 6 (0,5 điểm). Giữa hai điểm B và C có một cái ao (hình vẽ). Để đo khoảng cách BC người ta đo
được các đoạn thẳng
AD = 2m, BD = 10m, DE = 5m. Biết DE // BC. Tính khoảng cách giữa hai điểm B và C.
0,4 km
0,32 km
H
A
B
C