TRƯỜNG THCS LƯƠNG THẾ VINH NHÓM TOÁN
1
ĐỀ CƯƠNG ÔN TẬP TOÁN 8 – HK1 2023-2024
PHẦN 1: MỤC TIÊU
1. Kiến thức và kĩ năng:
• ĐẠI SỐ:
✓ HS được ôn tập và củng cố lại các kiến thức, các phép tính cộng, trừ, nhân, chia đơn thức,
đa thức nhiều biến. bảy hằng đẳng thức đáng nhớ, các phương pháp phân tích đa thức
thành nhân tử - Áp dụng giải các dạng bài tập có liên quan.
✓ Vận dụng được các hằng đẳng thức để phân tích đa thức thành nhân tử ở dạng: vận dụng
trực tiếp hằng đẳng thức; Vận dụng được PTĐT thành nhân tử để tìm được x.
✓ Vận dụng hằng đẳng thức thông qua nhóm hạng tử và đặt nhân tử chung.
• HÌNH HỌC:
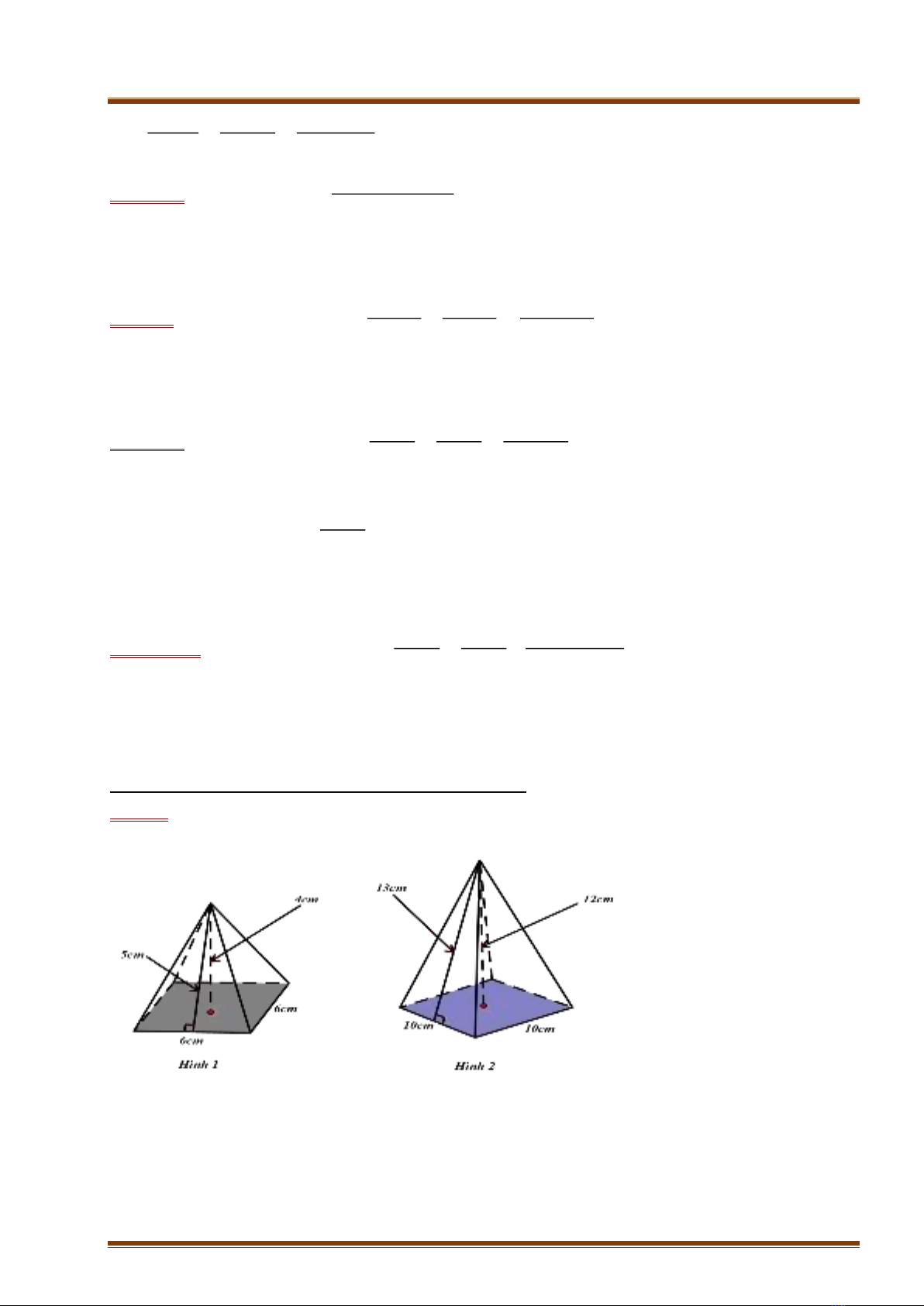
✓ HS ôn lại: Định nghĩa, tính chất cạnh, góc, mặt, công thức tính diện tích xung quanh,
tính thể tích của một số hình chóp tam giác, hình chóp tứ giác các tứ giác đặc biệt như:
hình
✓ HS ôn lại: Định nghĩa, các dấu hiệu nhận biết, tính chất các tứ giác đặc biệt như: hình
thang, hình thang cân, hình bình hành, hình chữ nhật, hình thoi, hình vuông.
✓ Giải quyết được một số vấn đề thực tin (đơn giản, quen thuộc) gắn với việc vận dụng
định lí pythagore, định lí đường trung tuyến của tam giác. Vận dụng công thức tính thể
tích, tính diện tích xung quanh của hình chóp.
✓ Rèn luyện kĩ năng vẽ hình, phân tích đề bài tìm hướng giải, kĩ năng trình bày bài cho
HS.
• DỮ LIỆU – BIỂU ĐỒ:
✓ Nhận biết mục đích biểu din dữ liệu bằng mỗi loại biểu đồ.
✓ Chuyển được dữ liệu từ dạng biểu din này sang dạng biểu din khác.
✓ Lựa chọn biểu đồ phù hợp để biểu din dữ liệu cho trước.
2. Thái độ:
✓ Cẩn thận, trung thực, hứng thú với môn học.
PHẦN 2: NỘI DUNG ÔN TẬP
I. PHẦN ĐẠI SỐ:
Bài 1: Rút gọn biểu thức
1) x(x – y) + y(x + y)
7) (x + 1)2 – (x – 2)(x + 2)
2) x(2x + 1) – (x2 – x + 3)
8)
( ) ( )( )
2
2x 1 x 5 x 5− − + −
3) x2y(2x3 - xy2 - 1);
9)
( )
2
x 2 2x 8+ + −
4) x(1,4x - 3,5y);
10)
( )
33
2x y x 2x 2
− − −
5) xy( x2 - xy + y2)
6) (1 - x2).(3 -5x);
11)
( )( )
2x 5 3x 2−+
12) x(x + 1) – x2 + 5x
1
2
2
5
2
7
1
2
2
3
3
4
4
5