
UBND HUY N VĨNH B OỆ Ả Đ GIAO L U HSG HUY N C P THCSỀ Ư Ệ Ấ
PHÒNG GIÁO D C VÀ ĐÀOỤ
T OẠ
MÔN TOÁN 8
(Đ có 1 trang)ềTh i gian làm bài 150 phútờ
Bài 1. (3 đi m)ể
a)Phân tích đa th c ứ thành nhân t .ử
b)Cho a;b;c là ba s đôi m t khác nhau th a mãn:. ố ộ ỏ
Tính giá tr c a bi u th c: P=.ị ủ ể ứ
c)Cho x + y + z = 0. Chứng minh rằng : 2(x5 + y5 + z5) = 5xyz(x2 + y2 + z2).
Bài 2. (2 đi m)ể
a) Tìm s t nhiên đ và là hai s chính ph ng.ố ự ể ố ươ
b) Cho a, b > 0 th a mãn . Ch ng minh .ỏ ứ
Bài 3. (1 đi m)ể
Cho hình bình hành ABCD có góc ABC nh n. V ra phía ngoài hình bình hành các ọ ẽ
tam giác đu BCE và DCF. Tính s đo góc EAF.ề ố
Bài 4. (3 đi m)ể
Cho tam giác ABC nh n có các đng cao AA’, BB’, CC’ và H là tr c tâmọ ườ ự
a) Ch ng minh BC’.BA + CB’.CA=BCứ2
b) Ch ng minh r ngứ ằ
c) G i D là trung đi m c a BC. Qua H k đng th ng vuông góc v i DH c t AB,ọ ể ủ ẻ ườ ẳ ớ ắ
AC l n l t t i M và N. Ch ng minh H là trung đi m c a MN.ầ ượ ạ ứ ể ủ
Bài 5. (1 đi m)ể
Cho hình vuông ABCD và 2018 đng th ng cùng có tính ch t chia hình vuông này ườ ẳ ấ
thành hai t giác có t s di n tích b ng . Ch ng minh r ng có ít nh t 505 đng th ng trong ứ ỉ ố ệ ằ ứ ằ ấ ườ ẳ
2018 đng th ng trên đng quy.ườ ẳ ồ
-----H t -----ế
Giám th s 1ị ố Giám th s 2ị ố
............................................ ............................................
UBND HUY N VĨNH B OỆ Ả GIAO L U H C SINH GI I C P THCSƯ Ọ Ỏ Ấ
PHÒNG GIÁO D C VÀ ĐÀOỤ
T OẠ
ĐÁP ÁN VÀ BI U ĐI M MÔN TOÁN 8Ể Ể
(Đ có 1 trang)ề
Bài 1 L i gi i s l cờ ả ơ ượ Đi m chi ti tể ế C ngộ
Bài 1
( 3 đi m)ể
a) =
=
==
==
0,25
0,25
0,25
0,25
1,0
b) (a+b+c)2=
T ng t : ; ươ ự
0,25
0,25
0,25
0,25
1,0

c) Vì x + y + z = 0
nên x + y = –z
(x + y)3 = –z3
Hay x3 + y3 +
3xy(x + y) = –z3
3xyz = x3 + y3 + z3
Do đó : 3xyz(x2 +
y2 + z2) = (x3 + y3 +
z3)(x2 + y2 + z2)
= x5 + y5 + z5 +
x3(y2 + z2) + y3(z2 +
x2) + z3(x2 + y2)
Mà x2 + y2 = (x +
y)2 – 2xy = z2 –
2xy (vì x + y = –z).
Tương tự:y2 + z2 =
x2 – 2yz ; z2 + x2 =
y2 – 2zx.
Vì vậy : 3xyz(x2 +
y2 + z2)
= x5 + y5 + z5 +
x3(x2 – 2yz) + y3(y2
– 2zx) + z3(z3 –
2xy) = 2(x5 + y5 +
z5) – 2xyz(x2 + y2 +
z2)
Suy ra : 2(x5 + y5 +
z5) = 5xyz(x2 + y2 +
z2
0,25
0,25
0,25
0,25
1,0
Bài 3 a) Đ và là hai sể ố
chính ph ngươ
và
Nh ng 59 là sư ố
nguyên t , nên: ố
T suy ra ừ
Thay vào , ta
đc .ượ
V y v i thì và làậ ớ
hai s chính ố
ph ng.ươ
0,25
0,25
0,25
0,25
1,0
b) Có: (*)
(D u đng th cấ ẳ ứ
x y ra khi a = b)ả
Áp d ng (*), có: ụ
Suy ra:
( Vì a+b = 1)
V i a, b d ng,ớ ươ
ch ng minh(Vìứ
a+b = 1)
(D u đng th cấ ẳ ứ
x y ra khi a = b)ả
Ta đc: ượ
D u đng th cấ ẳ ứ
x y ra: ả
0,25
0,25
0,25
0,25
1,0
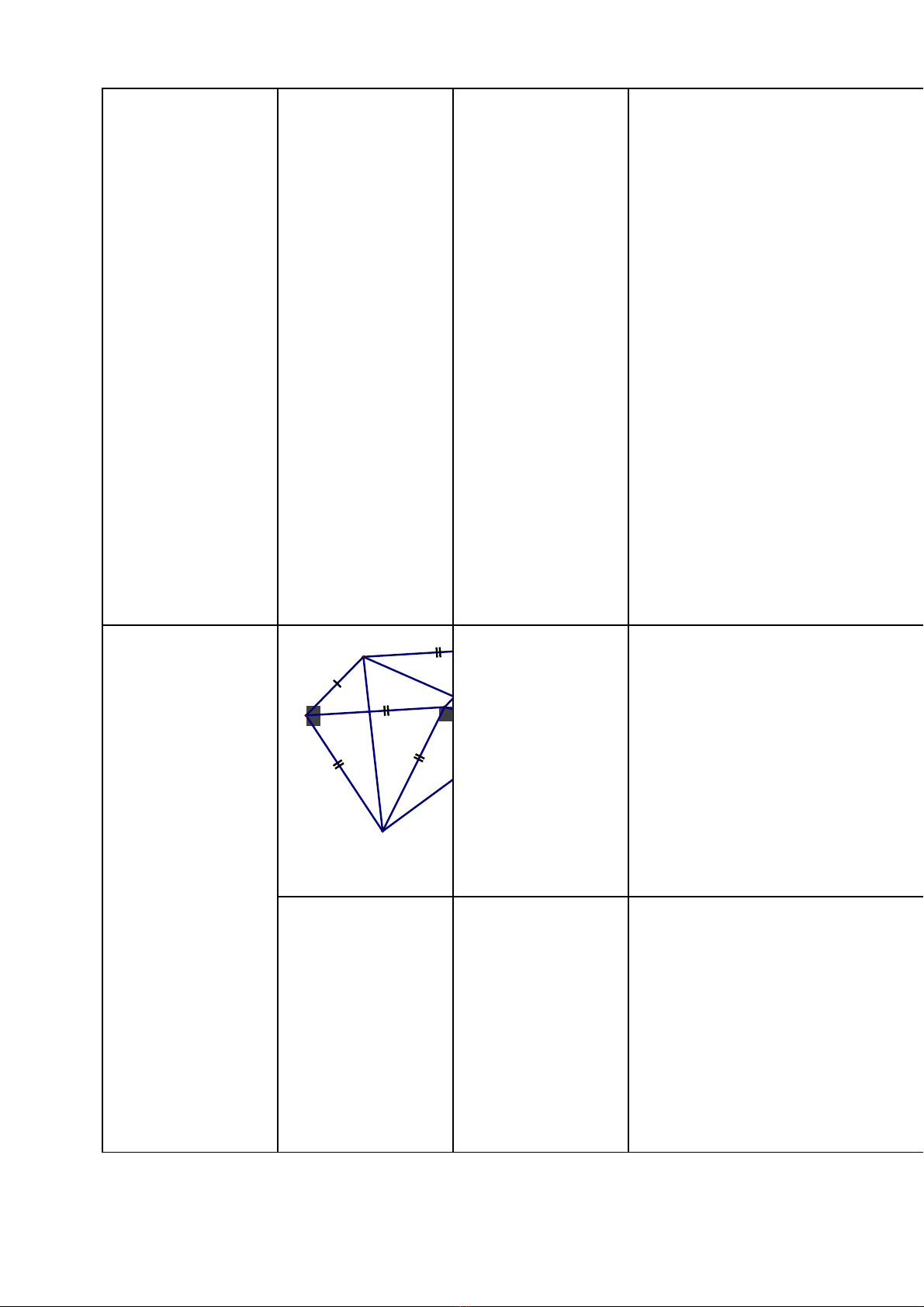
Bài 3
F
E
C
A
D
B
Ch ng minh đc ứ ượ
Ch ng minh đc ứ ượ
=>AE=EF
T ng t AF=EFươ ự
=>AE=EE=AF
=>Tam giác AEF
đuề
=>
0,25
0,25
0,25
0,25
1,0
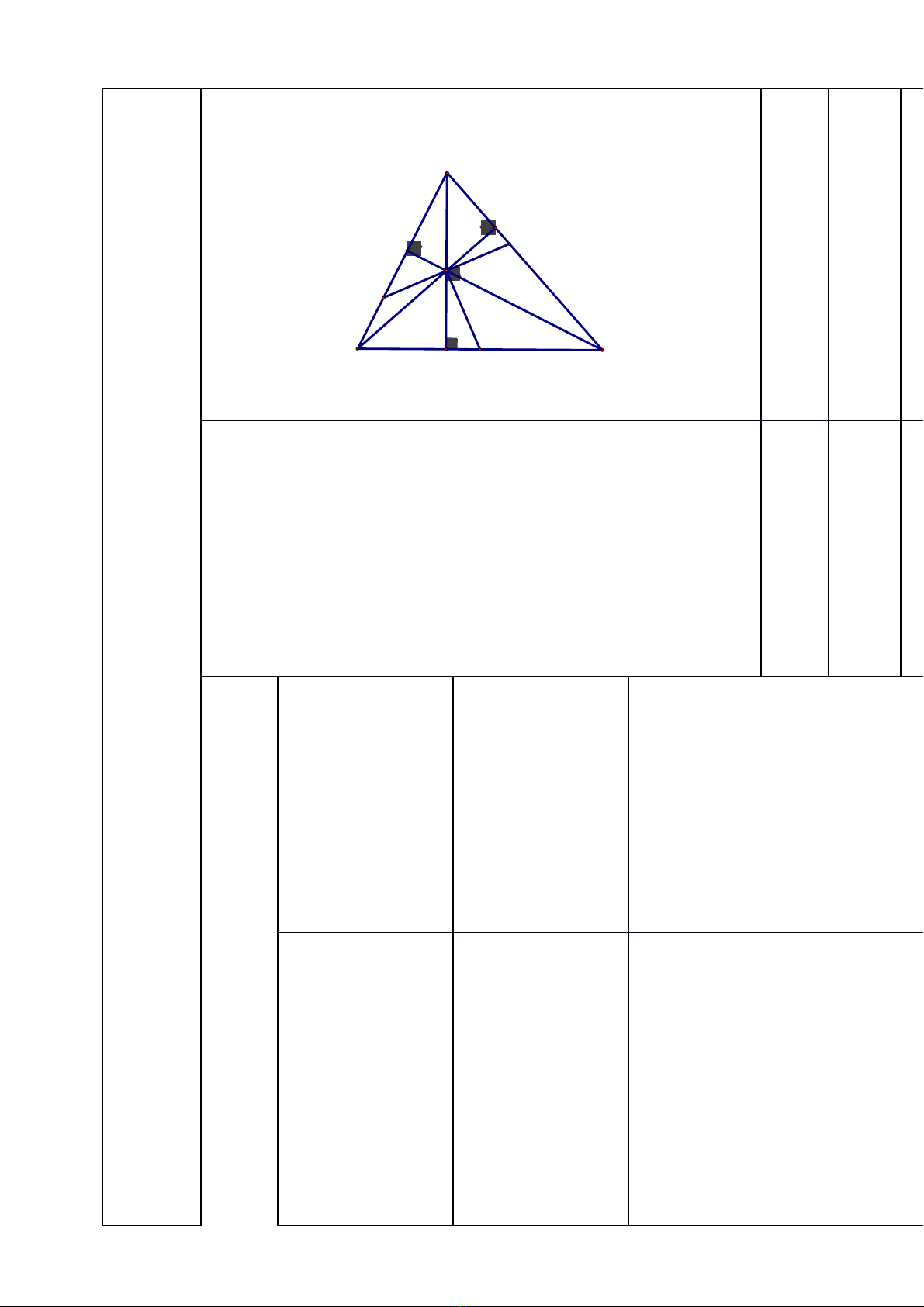
Bài 4
(3 đi m)ể
N
M
D
H
C'
B'
A'
B
C
A
a)Ch ng minh đng d ng v iứ ồ ạ ớ
=>=> (1)
Ch ng minhđng d ng v iứ ồ ạ ớ
=> (2)
T (1) và (2) =>ừ
T ng tươ ự
=>
0,25
0,25
0,25
0,25
1,0
b) Có =>
T ng t và ươ ự
=>
https://nguyenthien
huongvp77.violet.v
n/
0,25
0,25
0,5
1,0
c) Ch ng minh ứ
đc đng d ng ượ ồ ạ
v i (g-g)ớ
=> (3)
Ch ng minh đc ứ ượ
đng d ng v i (g-ồ ạ ớ
g)
=> (4)
Mà CD=BD (gt)
(5)
T (3), (4), (5) ừ
=>=> HM=HN
0,25
0,25
0,25
0,25
1,0
















