S GIÁO D C VÀ ĐÀO T OỞ Ụ Ạ
Đ CHÍNH TH CỀ Ứ
(Đ thi có 07 trang)ề
Đ KH O SÁT CH T L NGỀ Ả Ấ ƯỢ
TR NG THPT ƯỜ M.V. LÔ MÔ NÔ X PỐ
NĂM H C: 2019 - 2020Ọ
Bài thi: TOÁN
Th i gian làm bài: 90 phút, không k th i gian phát đờ ể ờ ề
H , tên thí sinh:ọ .....................................................................
S báo danh:ố ..........................................................................
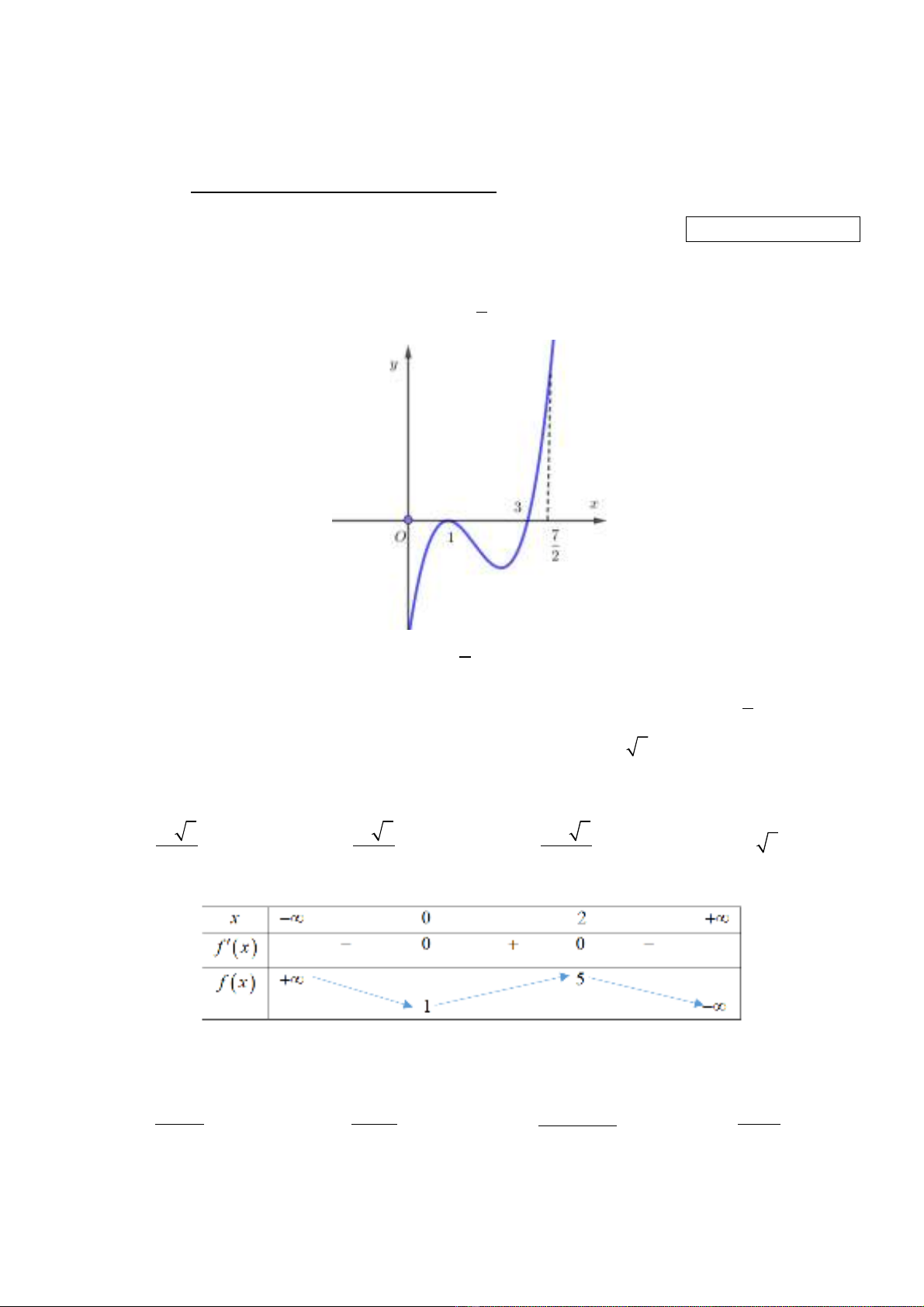
Câu 1. Cho hàm s ố
( )
y f x
=
liên t c trên đo n ụ ạ
7
0; 2
� �
� �
� �
có đ thồ ị
( )
'y f x
=
nh hình v .ư ẽ
Hàm s ố
( )
y f x
=
đt giá tr l n nh t trên đo n ạ ị ớ ấ ạ
1;3
2
� �
� �
� �
t i đi m ạ ể
0
x
nào d i đâyướ ?
A.
0
0x
=
.B.
0
3x
=
.C.
0
1x
=
.D.
0
1
2
x
=
.
Câu 2. Cho hình chóp
có đáy
ABCD
là hình vuông c nh ạ
2a
. C nh bên ạ
SA
vuông góc
v i ớ
m t ph ng ặ ẳ
và
3SC a
=
. Th tích kh i chóp ể ố
là
A.
3
5
6
a
V=
.B.
3
5
3
a
V=
.C.
3
2 5
3
a
V
=
.D.
3
5V a
=
.
Câu 3. Cho hàm s ố
( )
y f x
=
có b ng bi n thiên nh sau: ả ế ư
Hàm s đt c c ti u t i đi mố ạ ự ể ạ ể
A.
5x
=
.B.
1x
=
.C.
0x
=
.D.
2x
=
.
Câu 4 . Đng th ng ườ ẳ
3y
=
là ti m c n ngang c a đ th nào d i đây?ệ ậ ủ ồ ị ướ
A.
3 3
2
x
yx
−
=− +
.B.
3 3
2
x
yx
−
=+
.C.
2
2 3
1
x x
yx
+ +
=+
.D.
1
1 3
x
yx
+
=−
.
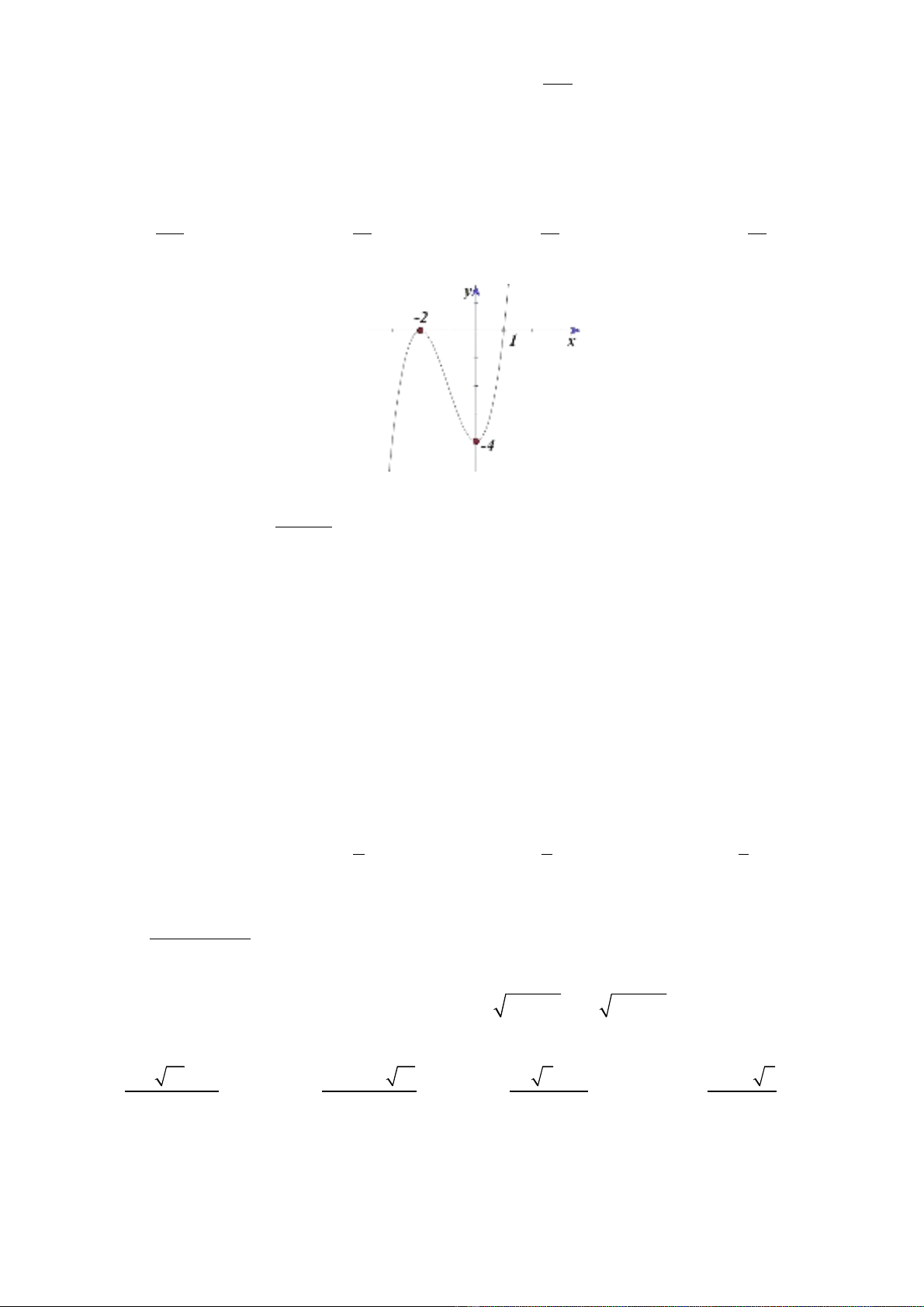
Câu 5. Cho hàm s ố
( )
y f x
=
có đ th là đng cong trong hình d i đây. ồ ị ườ ướ
Mã đ thi 001ề
Hàm s ố
( )
y f x
=
đng bi n trên kho ngồ ế ả
A.
( )
1; 2
.B.
( )
2;
+
.C.
( )
0;2
.D.
( )
;1
−
.
Còn r t nhi u đ mi n phí và các tài li u s p t i chia s các th y cô và các em có th vào linkấ ề ề ễ ệ ắ ớ ẽ ầ ể
bên d i đ download thêm ướ ể ạ
Link download: 15 Đ Thi Th THPT Qu c Gia 2020 file Word l n 1ề ử ố ầ
https://youtu.be/8ooz2N_k-JQ
Link download: 15 Đ Thi Th THPT Qu c Gia 2020 file Word l n 2ề ử ố ầ
https://youtu.be/OYzr7Y1_0eY
Câu 6. Cho hình chóp đu ề
.S ABC
có đáy
ABC
là tam giác đu c nh ề ạ
a
có góc gi a m t bên và m tữ ặ ặ
đáy
b ng ằ
0
60
. Th tích ể
V
c a kh i chóp ủ ố
.S ABC
là:
A.
3
3
24
a
V=
.B.
3
3
12
a
V=
.C.
3
3
8
a
V=
.D.
3
3
4
a
V=
.
Câu 7. Cho hàm s ố
( )
y f x
=
có đo hàm liên t c trên ạ ụ
ﾡ
. Đ th hàm s ồ ị ố
( )
y f x
=
nh hình v sau:ư ẽ
S đi m c c tr c a hàm s ố ể ự ị ủ ố
( )
3y f x x
= −
là
A.
2
.B.
4
.C.
3
.D.
1
.
Câu 8. Cho hình chóp
.S ABC
. Trên
,SB SC
l n l t l y hai đi m ầ ượ ấ ể
,H K
sao cho
2 3HS HB
=
,
5
7
SK SC=
. Khi đó t s th tích ỉ ố ể
.
.
S AHK
S ABC
V
V
b ngằ
A.
1
6
.B.
3
7
.C.
10
21
.D.
7
20
.
Câu 9. Cho hàm s ố
( )
y f x
=
xác đnh, liên t c trên và có b ng bi n thiên sauị ụ ả ế
x
−
0
+
y
– +
y
–2 2
–5
Trong các kh ng đnh sau kh ng đnh nào đúngẳ ị ẳ ị
A. Giá tr nh nh t c a hàm s b ng ị ỏ ấ ủ ố ằ
2
−
.
B. Giá tr l n nh t c a hàm s b ng ị ớ ấ ủ ố ằ
2
.
C. Giá tr l n nh t c a hàm s b ng ị ớ ấ ủ ố ằ
2
−
và
2
.
D. Giá tr nh nh t c a hàm s b ng ị ỏ ấ ủ ố ằ
5−
.
Câu 10. Hàm s ố
4 2
2 3y x x
= − + −
đng bi n trong kho ng nào sau đâyồ ế ả
A.
( )
; 1− −
và
( )
0;1
.B.
( )
;0−
.
C.
( )
1;1
−
và
( )
1;
+
.D.
( )
1;1
−
.
Câu 11. Giá tr l n nh t và giá tr nh nh t c a hàm s ị ớ ấ ị ỏ ấ ủ ố
4
2
x
yx
+
=−
trên đo n ạ
[ ]
3; 4
là
M
và
m
, khi đó
2M m
−
b ngằ
A.
3
.B.
2
−
.C.
4
−
.D.
1
−
.
Câu 12. Hàm s nào trong các hàm s d i đây đng bi n trên ố ố ướ ồ ế
ﾡ
?
A.
tany x
=
.B.
4 2
1y x x
= + −
.
C.
3 2
3 11y x x x
= − + +
.D.
.
Câu 13. Cho hàm s ố
3 2
1
x
yx
−
=−
có đ th là (C). T a đ giao đi m c a hai ti m c n làồ ị ọ ộ ể ủ ệ ậ
A.
( )
I 1; 2 .
B.
2
I ;3 .
3
� �
� �
� �
C.
( )
I 1;3 .
D.
( )
I 3;1 .
Câu 14. Bi t hàm s ế ố
3 2
( )f x x ax bx c
= + + +
đt c c đi t i ạ ự ạ ạ
0x
=
và
(1) 3f
= −
, đng th i đ th c aồ ờ ồ ị ủ
hàm s c t tr c tung t i đi m có tung đ b ng ố ắ ụ ạ ể ộ ằ
1−
. Tính giá tr c a ị ủ
( 2).f
−
A.
( 2) 21.f
− = −
B.
( 2) 3.f
− =
C.
( 2) 15.f
− =
D.
( 2) 19.f
− =
Câu 15. M t ph ng trình ti p tuy n c a đ th hàm s ộ ươ ế ế ủ ồ ị ố
( )
2 1
:2
x
C y x
+
=+
vuông góc v i đng th ngớ ườ ẳ
: y 3 2x
∆ = − +
là:
A.
1 2
3 3
y x
= +
.B.
1 4
3 3
y x= +
.C.
1 2
3 3
y x
= −
.D.
1 4
3 3
y x= −
.
Câu 16. Cho hàm s ố
2x m
yx m
+
=−
có đ th là ồ ị
( )
m
C
. Giá tr c a tham s ị ủ ố m đ đ th ể ồ ị
( )
m
C
đi qua đi mể
( )
2; 1A−
là:
A.
0m
=
.B.
4m
= −
.C.
4m
=
.D.
1
4
m
= −
.
Câu 17. Có bao nhiêu giá tr nguyên c a m đ hàm s ị ủ ể ố
( )
3
2
2 3 1
3
x
y mx m x
−
= + − + +
ngh ch bi n trênị ế
ﾡ
A.
4
.B.
2
.C.
5
.D.
3
.
Câu 18. Cho hình lăng tr đng ụ ứ
. ' ' 'ABC A B C
có đáy
ABC
là tam giác đu c nh a. Góc gi a ề ạ ữ
'A C
và
m t đáy b ng ặ ằ
30
o
. Th tích ể
V
c a kh i lăng tr ủ ố ụ
. ' ' 'ABC A B C
là:
A.
3
3
4
a
V
=
.B.
3
2
a
V
=
.C.
3
4
a
V
=
.D.
3
12
a
V
=
.
Câu 19. Đ th hình bên là c a hàm s nào d i đây?ồ ị ủ ố ướ
A.
3 2
3 4.y x x
= + +
B.
3 2
3 4.y x x
= + −
C.
3 2
3 4.y x x
= − + −
D.
3 2
3 4.y x x
= − −
Câu 20. Cho hàm s ố
1
3
mx
yx m
− +
=+
v i tham s ớ ố
0.m
Giao đi m c a hai đng ti m c n c a đ thể ủ ườ ệ ậ ủ ồ ị
hàm s thu c đng th ng có ph ng trình nào d i đây?ố ộ ườ ẳ ươ ướ
A.
3 0.x y
+ =
B.
3 0.x y
− =
C.
3 .y x
=
D.
3 0.x y
+ =
Câu 21. Hình l p ph ng có bao nhiêu c nh?ậ ươ ạ
A.
12
. B.
6
.C.
8
. D.
30
.
Câu 22. Cho hình chóp
.S ABC
có
SA
vuông góc v i m t ph ng đáy ớ ặ ẳ
7SA
=
. Tam giác
ABC
vuông t iạ
,B
5BA
=
,
6BC
=
. Th tích ể
V
c a kh i chópủ ố
.S ABC
là
A.
70
.B.
210
.C.
105
.D.
35
.
Câu 23. Hình lăng tr đng có đáy là hình thoi (không ph i hình vuông) có bao nhiêu m t đi x ng?ụ ứ ả ặ ố ứ
A.
5
.B.
2
.C.
4
.D.
3
.
Câu 24. Cho kh i lăng tr có di n tích đáy là ố ụ ệ
B
, đ dài đng cao là ộ ườ
h
. Công th c tính th tích kh iứ ể ố
lăng tr đó là:ụ
A.
V Bh
=
.B.
1
6
V Bh
=
.C.
1
2
V Bh
=
.D.
.
Câu 25. T ng các giá tr nguyên c a tham s ổ ị ủ ố
m
đ đng th ng ể ườ ẳ
( )
: 3d y x
= − +
c t đ th hàm sắ ồ ị ố
( )
2
2 2
:1
x m m
C y x
+ −
=+
t i hai đi m phân bi t là :ạ ể ệ
A.
3
. B.
2
. C.
0
. D.
1
.
Câu 26. Cho hai s th c ố ự
,x y
th a mãn : ỏ
( )
3
9 2 3 5 3 5 0x y xy x xy
+ − − + − =
. Tìm giá tr nh nh tị ỏ ấ
c a ủ
( )
( )
3 3 2
6 3 3 1 2P x y xy x x y
= + + + + + −
?
A.
296 15 18
9
−
.B.
36 296 15
9
+
.C.
4 6 18
9
− +
.D.
36 4 6
9
−
.
Câu 27. Cho hình vuông
ABCD
có c nh b ng ạ ằ
a
và có di n tích ệ
1
S
. N i b n trung đi m ố ố ể
1 1 1 1
, , ,A B C D
theo th t là b n trung đi m c a ứ ự ố ể ủ
, , ,AB BC CD DA
ta đc hình vuông th hai ượ ứ
1 1 1 1
A B C D
có di n tíchệ
2
S
. Ti p t c nh th ta đc hình vuông th ba làế ụ ư ế ượ ứ
2 2 2 2
A B C D
có di n tích ệ
3
S
, … và c ti p t c nhứ ế ụ ư
th , ta tính đc các hình vuông l n l t có di n tích làế ượ ầ ượ ệ
4 5 100
, ,...S S S
(tham kh o hình v ). Bi t t ngả ẽ ế ổ
100
1 2 100 93
2 1
... 2
S S S
−
+ + + =
. Tính
?a
A.
2a
=
.B.
8a
=
.C.
4a
=
.D.
1a=
.
Câu 28. Cho
,a b
là s th c d ng. Kh ng đnh nào sau đây sai?ố ự ươ ẳ ị
A.
( )
. .
nn n
a b a b
=
.B.
mm n
n
aa
a
−
=
.C.
.m n m n
a a a
+ =
.D.
( )
.
n
m m n
a a=
.
Câu 29. Ph ng trình ươ
sin 5 cos 5 2x x- =-
cón ghi m là ệ
( )
2,x k k
a b
p p
= + ﾡ ?
trong đó
aﾡ?
và
b
là s nguyên t . Tính ố ố
3a b+
?
A.
3 10a b+ =
.B.
3 5a b+ = -
.C.
3 7a b+ =-
.D.
3 12a b+ =
.
Câu 30. Cho hình chóp
.S ABC
có đáy là tam giác vuông t i ạ
B
,
2, 2AC BC= =
. C nh bên ạ
SB
vuông góc v i đáy và ớ
. Bi t kho ng cách t ế ả ừ
B
đn m t ph ng ế ặ ẳ
( )
SAC
b ng ằ
3a
b
, trong đó
,a b
là hai s nguyên t cùng nhau. Khi đó ố ố
a b-
b ng:ằ
A.
1
.B.
3
−
.C.
3
.D.
1-
.
Câu 31. Bà Vui g i vào ngân hàng s ti n 300 tri u đng theo th th c lãi kép v i lãi su t 1,5% m tử ố ề ệ ồ ể ứ ớ ấ ộ
quý. Gi đnh lãi su t không thay đi trong su t quá trình g i thì bà Vui nh n đc s ti n c g c l nả ị ấ ổ ố ử ậ ượ ố ề ả ố ẫ
lãi là bao nhiêu sau hai năm k t ngày g i?ể ừ ử
A. 328032979 đng.ồB.
309067500 đng.ồC.
337947776 đng.ồD.
336023500 đng.ồ
Câu 32. Tìm h s c a ệ ố ủ
8
x
trong khai tri n thành đa th c c a ể ứ ủ
2
(3 2 )
n
x
−
, bi t n là s nguyên d ngế ố ươ
th a mãn ỏ
0 2 4 2
2 1 2 1 2 1 2 1
... 1024
n
n n n n
C C C C
+ + + +
+ + + + =
A.
.B.
103680
.C.
130260
.D.
130260
−
.
Câu 33. S h ng không ch a ố ạ ứ
x
trong khai tri n ể
9
2
3
xx
� �
+
� �
� �
là
A.
4 4
9
3 C
.B.
3 3
9
3 C
. C.
6 6
9
3 C
. D.
2 2
9
3 C
.
Câu 34. Cho hình chóp
.S ABC
có
SB
vuông góc v i m t đáy, ớ ặ
SB a
=
; tam giác
ABC
vuông cân t iạ
,A
2AB a=
. G i ọ
,M N
l n l t thu c các c nh ầ ượ ộ ạ
,SA SC
sao cho
1,
2
SM MA SN NC
= =
uuur uuur
. Tính th tíchể
kh i chóp ố
.B ACNM
.
A.
3
7
9
a
. B.
3
5
9
a
.C.
3
5
18
a
. D.
3
7
18
a
.
Câu 35. Cho hình chóp t giác ứ
. G i ọ
I
và
J
l n l t là trung đi m c a c nh ầ ượ ể ủ ạ
SB
và
SD
.
Kh ng đnh nào sau đây đúng?ẳ ị
A.
IJ
/ /
mp
( )
SCD
.B.
( )
/ / IJ mp SAB
.