Bài 1. (2 đi m)ể
1. Tìm x đ các bi u th c sau có nghĩa.ể ể ứ
a)
52
x
b)
32
1
1
x
x
2. Rút g n các bi u th c sau:ọ ể ứ
a)
1
75 48 300
2
A
= + −
b)
� �
� �
� �
� �
= + −
+ −
2
:9
3 3
x x x
Bx
x x
(v i xớ
0 và x
9)
Bài 2. (1,5 đi m) ểCho hàm s y = ố(m - 2)x + 3 (d)
a) Xác đnh m bi t (d) đi qua A(1; -1). V đ th hàm s v i m v a tìm đc.ị ế ẽ ồ ị ố ớ ừ ượ
b) Vi t ph ng trình đng th ng đi qua đi m B(-2; 2) và song song v iế ươ ườ ẳ ể ớ
đng th ng v a tìm đc câu a.ườ ẳ ừ ượ ở
Bài 3. (2,0 đi m)ể
a) Gi i ph ng trình: ả ươ
021
2
xx
b) Cho pt đng th ng 2x – y = 3 (d) và pt đng th ng x + y = 6 (d’). ườ ẳ ườ ẳ Gi iả
h ph ng trình g m đng th ng (d) và (d')?ệ ươ ồ ườ ẳ
c) Bóng c a m t cây trên m t đt là 12m, tia n ng m t tr i chi u xiên m tủ ộ ặ ấ ắ ặ ờ ế ộ
góc 300 so v i m t đt. Tính chi u cao c a cây?ớ ặ ấ ề ủ
Bài 4. (3,5 đi m)ể
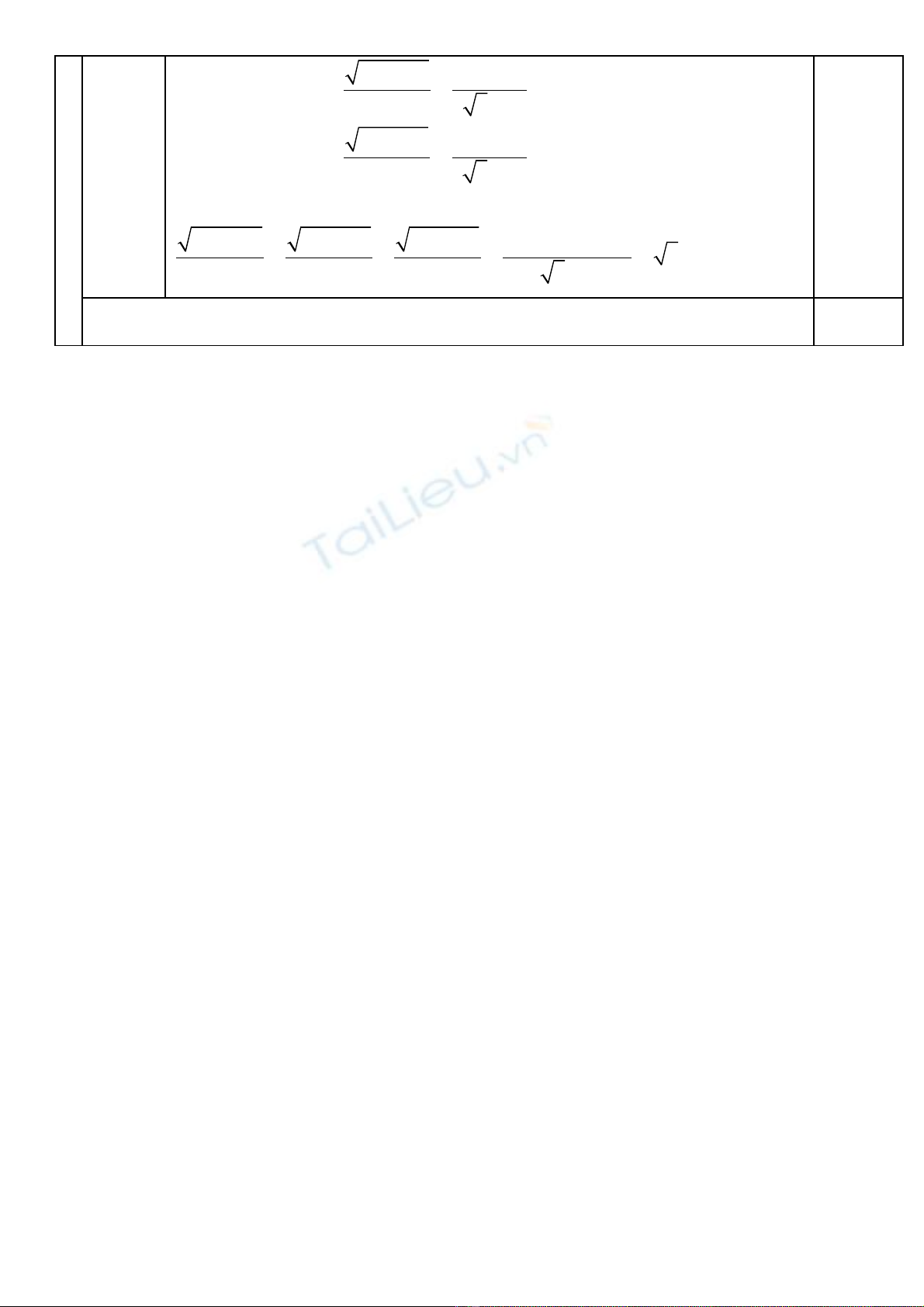
Cho đng tròn (O;R) đng kính AB. Qua A và B v l n l t hai ti pườ ườ ẽ ầ ượ ế
tuy n (d) và (d’) v i đng tròn (O). M t đng th ng đi qua O c t đng th ngế ớ ườ ộ ườ ẳ ắ ườ ẳ
(d) M và c t đng th ng (d’) P. T O k m t tia vuông góc v i MP và c tở ắ ườ ẳ ở ừ ẻ ộ ớ ắ
đng th ng (d’) N. K OI ườ ẳ ở ẻ MN t i Iạ.
a) Ch ng minh: OM = OP và ứNMP cân
b) Ch ngứ minh: OI = R và MN là ti p tuy n c a đng tròn (O)ế ế ủ ườ .
c) Tính
d) Tìm v trí c a M đ di n tích t giác AMNị ủ ể ệ ứ B là nh nh tỏ ấ ?
Bài 5. (1,0 đi m)ể
a) Cho a, b > 0; Ch ng minh r ng: 3(bứ ằ 2 + 2a2) (b + 2a)2
b) Cho a, b, c > 0 th a mãn ab + bc + ca = abc. ỏ
Ch ng minh r ng: ứ ằ
2 2 2 2 2 2
b 2a c 2b a 2c 3
ab bc ca
+ + +
+ +
.
----------- H t -----------ế
(Cán b coi thi không gi i thích gì thêm)ộ ả
UBND HUY N VĨNH B OỆ Ả
PHONG GIAO DUC VA ĐAO TAO
Đ chính th cề ứ
ĐỀ KH O SÁT ẢH C KÌ IỌ
NĂM H C 201Ọ7 – 2018
MÔN: TOÁN 9
(Đ thi g m 0ề ồ 1 trang) (Th i gian:120 phút không k giao đờ ể ề)
1. H , tên thí sinh:.................................ọ
2. SBD:............Phòng thi s :................ố 1. Giám th 1:.......................................ị
2. Giám th 2:.........................................ị
Bài N i ộdung - đáp ánĐi mể
1
a
(0,5đ)
Bi u th c A = ể ứ
52 x
có nghĩa khi:
2
5
052 xx
V y ậ
5
2
x
thì bi u th c A có nghĩa.ể ứ 0,25x2
b
(0,5đ)
Bi u th c B = ể ứ
32
1
1
x
x
có nghĩa khi:
1
2
3
01
032
x
x
x
x
V y ậ
3
2
1
x
x
thì bi u th c A có nghĩa.ể ứ
0,25
0,25
c
(0,5đ)
1
75 48 300 5 3 4 3 5 3 4 3
2
A= + − = + − =
0,25x2
d
(0,5đ)
� �
� �
� �
� �
= + −
+ −
2
:9
3 3
x x x
Bx
x x
( ) ( )
( ) ( )
+ +
=
−
−
+ −
. .
.
3 3 2
:9
3 3
x x x x x
x
x x
−
= = =�
− − −
2 2 2 9
:
9 9 9 2
x x x x x
x x x x
0,25
0,25
2a
(1,0đ)
* Xét A(1; - 1) => x = 1 và y = - 1 thay vào (d) => m = - 2
V y (d) có ph ng trình là: y = - 4x + 3ậ ươ
* V đ th đt (d)ẽ ồ ị
- Xác đnh đúng t a đ hai đi mị ọ ộ ể
- V h tr c Oxy và đng th ng qua hai đi m chính xácẽ ệ ụ ườ ẳ ể
0,25
0,25
0,25
0,25
UBND HUY N VĨNH B OỆ Ả
PHONG GIAO DUC VA ĐAO TAO
(Đap an g m 0 ồ3 trang)
ĐÁP ÁN, BI U ĐI M CH M Ể Ể Ấ ĐÊ H C KỌ Ỳ I
MÔN: TOÁN 9
b
(0,5đ)
- Đng th ng c n tìm có d ng y = ax+ b (d') vì (d') // (d) => a = - 4; bườ ẳ ầ ạ
3 hay đng th ng (d') y = - 4x + b.ườ ẳ
- Mà (d') đi qua B(-2; 2) => x = - 2 và y = 2 th a mãn ph ng trình (d')ỏ ươ
=> b = - 6 (t/m). V y ph ng trình (d') c n tìm là: y = - 4x - 6ậ ươ ầ
0,25
0,25
3
a
(0,5đ)
021
2
xx
ĐK: x
0
0212
xxx
32
x
2
3
x
vì x
0
4
9
x
V y ậ
9
4
x
=
là nghi m c a pt.ệ ủ
0,25
0,25
b
(0,5đ)
T h ta có (d): y = 2x - 3 và (d'): y = - x + 6ừ ệ
- Xét ph ng trình hoành đ giao đi m:ươ ộ ể 2x - 3 = - x + 6
=> x = 3; thay x = 3 vào (d') => y = 3 => D(3; 3).
- V y giao đi m ậ ể c a (d) và (d') là Dủ(3; 3); h ph ng trình có nghi m ệ ươ ệ
(x; y) = (3; 3).
0,25
0,25
c
(1,0đ)
G i cây có chi u cao AB ọ ề (AB không âm) và có bóng trên m t đt làặ ấ
AC
Do cây tr ng vuông góc v i m t đt nên tam giác ồ ớ ặ ấ
ABC vuông t i Aạ
=> AB = AC.tanC = 12.tan 300 = 12.
3
1
= 4
3
(t/m)
V y cây đó cao 4ậ
3
m
0,25
0,25
0,25
0,25
4Vẽ
hình
(0,5đ)
B
d
d'
P
N
M
I
A
O
1
2
V hình đúng cho câu aẽ
0,5
a
(1,0đ)
* Xét AOM và BOP có:
Góc A b ng góc B ằ(cùng b ng 90ằ0)
OA = OB (cùng b ng R)ằ
Góc O1 b ng góc Oằ2(vì đi đnh)ố ỉ
0,25 ñ
AOM = BOP (g-c-g)
OM = OP
0,25 ñ
*NMP có: NO MP (gt) và OM = OP(cmt) NMP cân
0,25
0,25
0,25
0,25
b
(0,75đ)
Vì NMP cân nên NO là phân giác c a ủ
ﾷ
MNP
OI = OB = R (tính ch t đi m thu c tia phân giác )ấ ể ộ
0,25 ñ
Mà MN OI tai I (O)
MN là ti p tuy n c a (O)ế ế ủ
0,25
0,25
0,25
c
(0,75đ)
Vì OI = R (câu b)
=> I thu c đng tròn đng kính ABộ ườ ườ
=> AIB vuông t i Iạ
=>
ﾷ
AIB
=900
0,25
0,25
0,25
d
(0,5đ)
T giác AMNP là hình thang vuông :ứ
AMNB
(AM NB).AB (MI IN).2R
S MN.R
2 2
Mà R không đi, MN ổ AB
=> SAMNB nh nh t ỏ ấ MN nh nh tỏ ấ
0,25 ñ
MN = AB MN // AB
AMNB là hình ch nh tữ ậ
AM = NB = R
0,25
0,25
5a
(0,25đ)
3(b2 + 2a2) (b + 2a)2
2 2 2 2
3b 6a b 4ab 4a
+ + +� �
2
2(a b) 0
−� �
;
∀
a b
D u “=” x y ra khi và ch khi a = b.ấ ả ỉ
0,25
b
(0,75đ)
Theo câu a ta có:
2 2 2 2 2
2 2
b 2a
3(b 2a ) (b 2a) b 2a 3
b 2a bc 2ac (1)
ab 3abc
+
+ + +� � �
+ +
Ch ng minh t ngứ ươ t :ự
0,25
2 2
2 2
c 2b ca 2ab (2)
bc 3abc
a 2c ab 2bc (3)
ca 3abc
+ +
+ +
C ng (1), (2) và (3) vộ ế v iớ v ta đcế ượ
2 2 2 2 2 2
b 2a c 2b a 2c 3(ab bc ca) 3
ab bc ca 3abc
+ + + + +
+ + =
0,25
0,25
T ngổ10đ
Chú ý:
- H c sinh làm cách khác đúng v n cho đi m t i đa;ọ ẫ ể ố
- V hình sai không ch m, không v hình làm đúng ph n nào cho n a s đi m ph n đó;ẽ ấ ẽ ầ ử ố ể ầ
- Trong m t câu n u ph n trên sai thì không ch m ph n d i, đúng đn đâu cho đi m đn ộ ế ầ ấ ầ ướ ế ể ế
đó;
- Trong m t bài có nhi u câu, n u HS công nh n KQ câu trên làm câu d i mà đúng v n ch m ộ ề ế ậ ướ ẫ ấ
đi m./.ể
--------------------- H t------------------ế