1
ONTHIONLINE.NET
đề kiểm tra chất lượng
Môn: đại số 11
Câu 1(2đ)
a) Tỡm CSC biết:
2 5 3
4 6
10
26
a a a
a a
b) Tỡm CSN cú 6 số hạng biết tổng của 5 số hạng đầu bằng 31 và
tổng của 5 số hạng sau bằng 62
Câu 2(3 đ)
Tớnh cỏc giới hạn sau:
a). lim4.3n + 7n + 1
2.5n + 7n b). lim( nn2n
3 23 ) c) 3
1 2 3 ...
lim
1
n
n
d) 3 2
x 1
2x 7 3
lim
e) 2
3 2
lim 3 1
x
x x x
x

f) 3
2 3
x
lim ( x 1 x 1)
g)
2
33
lim 2
2
2
x
x
xx
x h) 2
0x
x
2
x3cosxcos
lim
Câu 3(2 đ) a) Tỡm a,b để hàm số sau liên tục trên R
f(x) =
3 xkhix 4
3x1 khi bax
1 x khi x2
b) Chứng minh rằng phương trỡnh: x3 – 3x2 + 3 = 0 cú 3
nghiệm trong khoảng (– 1;3)
Câu 4(3 đ) a) . Tìm đạo hàm cấp n của các hàm số sau:
1
2
23
2
2
x
x
xx
y
b) Cho hàm số f(x) = 2
x x 4
x 1
(1)
Viết phương trỡnh tiếp tuyến của đồ thị hàm số (1) biết tiếp tuyến đó
song song với đường thẳng y = -3x +2009
c) Giải phương trỡnh y’=0
với y = 3 cos5 2
sin5 sin3
5 5 3
x
x x
hết
2
đề kiểm tra chất lượng
Môn: hình học 11
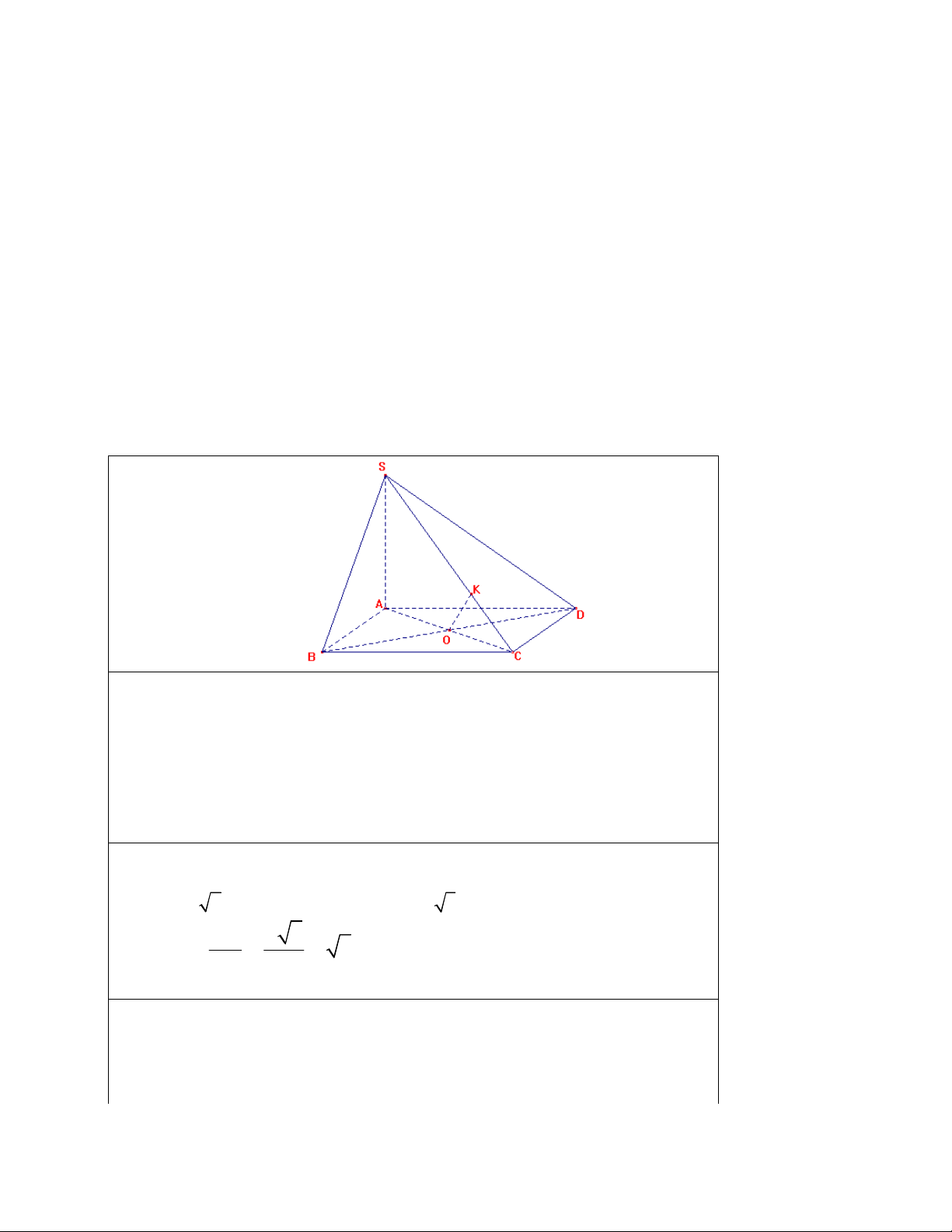
Bài 1 (3,0đ): Cho hình chóp S.ABCD, đáy là hình vuông và SA
(ABCD)
biết
SA =
2
a
và AB = a.
a, CMR: các mặt bên của hình chóp là tam giác vuông.
b, Tính góc giữa 2 đường thẳng AB, SC.
c, Gọi K là hình chiếu vuông góc của O trên SC CMR đoạn OK vuông
góc với cả SC và BD. Tính OK
Bài 2: . (4 điểm ) Cho hỡnh chúp S.ABCD cú
)
ABCD
(
SA
và
2
aSA
đáy ABCD là hỡnh thang vuụng tại A và B cú
a
AD
;
a
BC
AB
2
a) Chứng minh rằng: tam giỏc SCD vuụng.
b) Tớnh khoảng cỏch từ
A
đến mặt phẳng (SBC). .
c) Từ điểm I là trung điểm của AD ta dựng IJ vuông góc với SD (J
SD). Chứng minh: SD vuụng gúc với mặt phẳng (CIJ)
d) Tớnh gúc giữa hai mặt phẳng (SAD) và (SCD).
Bài 3: . (3 điểm ) Cho hỡnh choựp S.ABCD coự ủaựy ABCD laứ hỡnh thoi
caùnh a vaứ
0
60
BAD
. Goùi O laứ giao ủieồm cuỷa AC vaứ BD. ẹửụứng
thaỳng SO (ABCD) vaứ SO =
3
4
a
. Goùi E laứ trung ủieồm cuỷa BC, F laứ
trung ủieồm cuỷa BE.
a) Chửựng minh (SOF) (SBC).
b) Tớnh caực khoaỷng caựch tửứ O vaứ A ủeỏn (SBC).
Hết
3
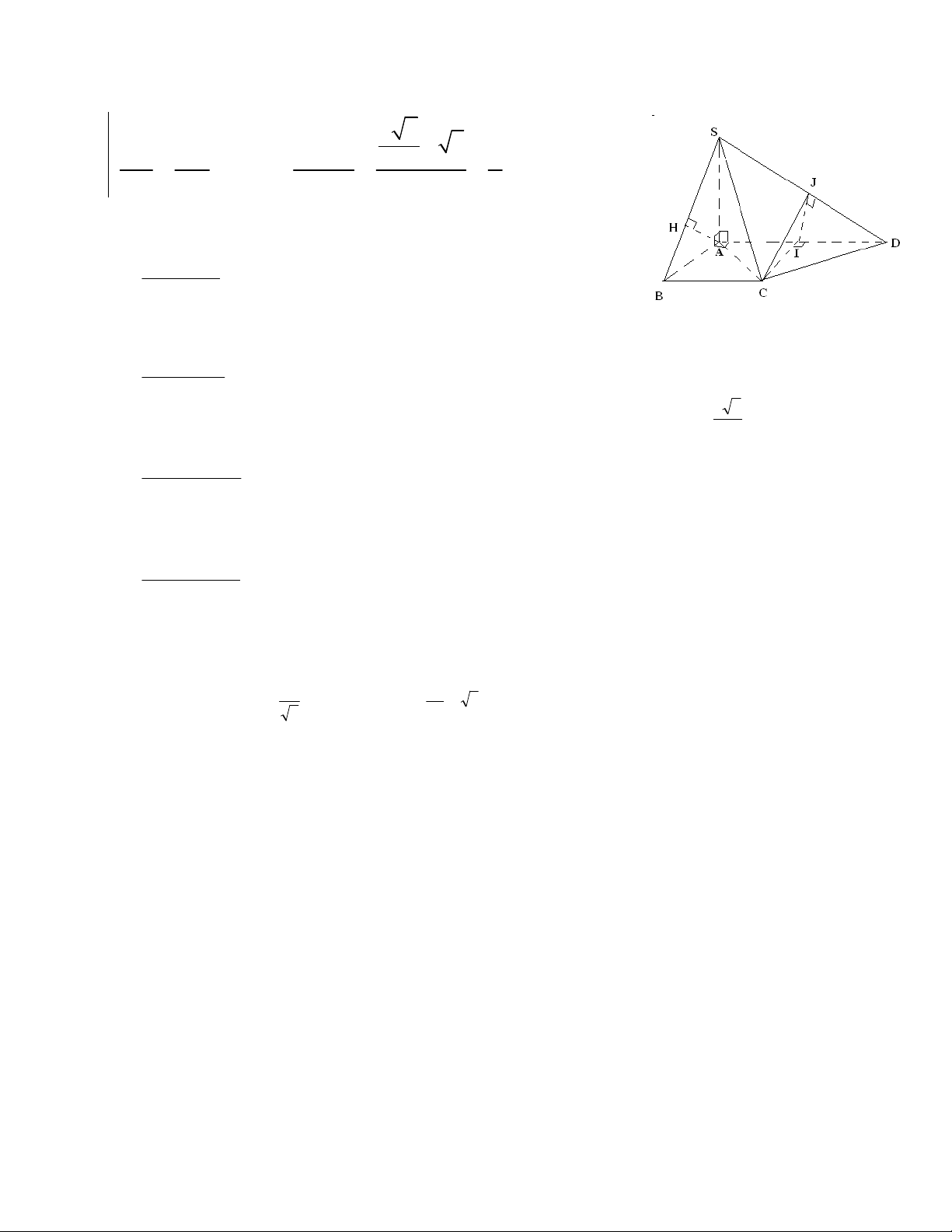
Bài1
Hình vẽ:
a. Vì
SA ABCD
nên
SA AB
,
SA AD
nên các tam giác
,
SAB SAD
là các tam giác vuông.
Ta có
SA CD
CD SAD CD SD
CD AD
nên tam giác
SCD
là
các tam giác vuông. Tương tự tam giác
SBC
là các tam giác vuông.
b. Ta có
//
AB CD
nên
, ,
AB SC CD SC SCD
.
Vì SA =
2
a
và AB=CD = a nên SD=
3
a
. Trong tam giác vuông SCD ta
có 3
tan 3
SD a
C
CD a
. Vậy
, 60
AB SC
c. Trong tam giác SAC dựng
,
OK SC K SC
Dễ thấy
BD SAC
nên
OK BD
. Vậy OK là đường vuông góc
chung cần tìm.
Ta có
COK CSA
nên
4
2. 2
.2
2 2
aa
CO OK CO SA a
OK
SC SA SC a
Vậy
,
2
a
d SC BD
.
Bài 2
)ñ;(SCD;SADgoùc
IJ
CI
CJItan;)ñ;(
a
IJTínhICIJ
)ñ;(CJIgoùcSCD;SADgoùc
SCDCJ;SADIJ
CIJSDSDCJ
SDIJ
SDSCDSAD
)ñ;(:dCaâu
)ñ;(CIJSD
SDIJmaø
)ñ;(SDCISADCI
SACI
AB//CIADCI
)ñ;(:cCaâu
)ñ;(
a
AH)SBC(;Ad)ñ;(SBCAH
AHBCSABBC
SABC
ABBC
SBAHdöïngSABTrong
)ñ(:bCaâu
)ñ;(CtaïiSCDACCD)ñ;()SAC(CD
CtaïicaânACDACCD
)ABCD(SASACD
)ñ;()BCADvaøBC//AD(roõHình
)ñ(:aCaâu
)
ñ
(
:
Baøi
25060350
3
50
251
250
50
750
50
3
6
50
1
25050
2502
1
4
4
0