1/5 - Mã đề 101
THPT SỐ 3 BẢO THẮNG
TỔ: TOÁN – TIN - CN
(Đề thi có 04 trang)
KIỂM TRA CUỐI KỲ 2 NĂM HỌC 2021 - 2022
MÔN TOÁN – Khối lớp 12
Thời gian làm bài : 90 phút
(không kể thời gian phát đề)
PHẦN I. TRẮC NGHIỆM (8 điểm)
Câu 1. Cho hàm số
( )
fx
có đạo hàm
( )
′
fx
liên tục trên đoạn
[ ]
2; 4
và thỏa mãn
( )
2 3,=f
( )
4 10=f
. Giá
trị của
( )
4
2
d
′
∫fxx
bằng
A.
. B.
7−
. C.
7
. D.
2
Câu 2. Cho hàm số
( )
fx
liên tục và không âm trên đoạn
[ ]
3; 6 .
Diện tích hình phẳng giới hạn bởi các
đường
( )
=y fx
,
0, 3yx= =
và
6x=
được tính theo công thức nào dưới đây?
A.
( )
6
3
d.S fx x=
∫
B.
( )
62
3
d.S fx x
π
=

∫
C.
( )
6
3
d.S fx x= −∫
D.
( )
6
3
d.S fx x
π
=
∫
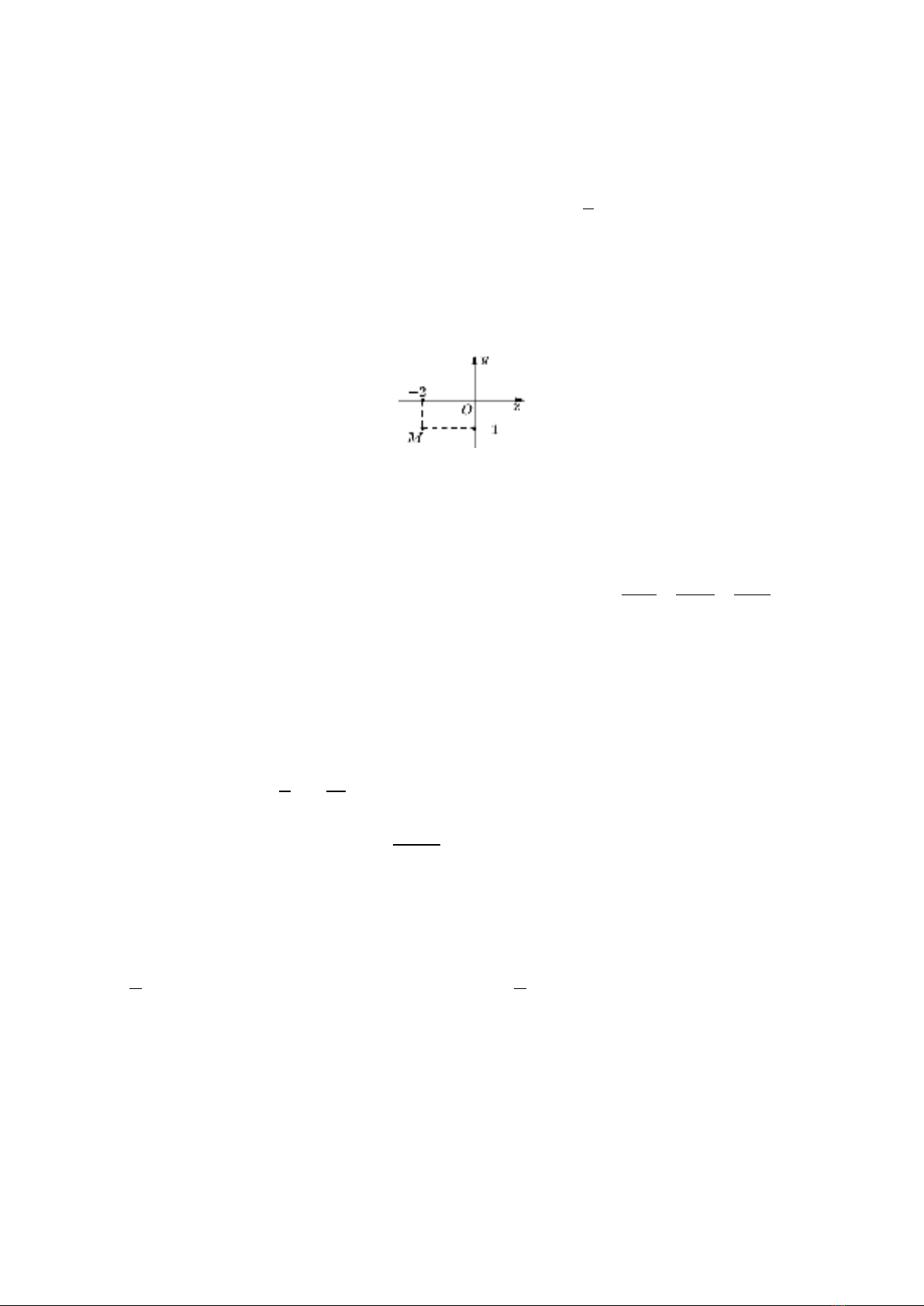
Câu 3. Điểm
( )
1; 2M−
là điểm biểu diễn số phức nào sau đây?
A.
2zi=−+
. B.
12zi= +
. C.
12zi= −
. D.
2zi=−−
.
Câu 4. Phần ảo của số phức
54= −zi
là
A.
5−
. B.
5
. C.
4
. D.
4−
.
Câu 5. Gọi
( )
H
là hình phẳng giới hạn bởi các đường
4 , 0, 3
x
y yx= = =
và
5x=
. Thể tích của khối tròn
xoay tạo thành khi quay
( )
H
quanh trục
Ox
bằng
A.
5
3
4d.
x
Vx=
∫
B.
5
3
4d.
x
Vx
π
=
∫
C.
5
2
3
4 d.
x
Vx
π
=∫
D.
5
2
3
4 d.
x
Vx=
∫
Câu 6. Trong không gian
Oxyz
, cho
3=+−OM i j k


. Tọa độ điểm
M
là
A.
( )
113−−−M;;
B.
( )
11 3−M;;
. C.
( )
113M;;
. D.
( )
11 3−−M;;
.
Câu 7. Trong không gian
Oxyz
, đường thẳng
∆
đi qua hai điểm
( )
1; 2; 3A−
và
( )
2; 1; 4B
có phương trình
là
A.
1
23
3
xt
yt
zt
= +
=−+
= +
. B.
1
23
3
xt
yt
zt
= −
=−+
= +
. C.
1
23
3
xt
yt
zt
= +
=−−
= +
. D.
1
23
3
xt
yt
zt
= +
=−+
= −
.
Câu 8. Cho số phức
2zi= −
. Tính
z
.
A.
5z=
. B.
5z=
. C.
3z=
. D.
3z=
.
Câu 9. Phần thực của số phức
78zi=−−
bằng
A.
8
. B.
8−
. C.
7
. D.
7−
.
Câu 10. Số phức liên hợp của số phức
23i−
là
A.
23i−
. B.
23i−−
. C.
23i+
. D.
23i−+
.
Câu 11. Trong không gian
Oxyz
, đường thẳng
( )
2 ,
3
:
14
xt
yt
zt
= +
∆= ∈
= −
có một vectơ chỉ phương là
Mã đề 101
2/5 - Mã đề 101
A.
( )
1
1; 2; 4u= −
B.
( )
41; 0; 4u= −
C.
( )
2
3; 2;1u=
D.
( )
31; 2; 4u=−−
Câu 12. Cho hai số phức
15= +zi
và
67= −wi
. Số phức
+zw
bằng
A.
72i+
. B.
72i−
. C.
7 12i−
. D.
7 12i+
.
Câu 13. Cho hàm số
( )
fx
liên tục trên
.
Mệnh đề nào dưới đây đúng?
A.
( ) ( )
5d d=
∫∫
fx x fx x
B.
( ) ( )
1
5d d
5
=
∫∫
fx x fx x
C.
( ) ( )
5 d5 d=
∫∫
fx x fx x
D.
( ) ( )
5 d5 d= +
∫∫
fx x fx x
Câu 14. Cho hai số phức
1
24= −zi
,
2
48=−+zi
. Khi đó số phức
12
−zz
bằng
A.
6 12i+
. B.
64i−
. C.
6 12i−
. D.
64i+
.
Câu 15. Số phức có hình biểu diễn là điểm
M
trong hình vẽ bên là
A.
12zi=−+
B.
2zi=−+
C.
12zi=−−
D.
2zi=−−
Câu 16. Biết
( )
4
3
d3=
∫fx x
. Giá trị của
( )
4
3
9d
∫fx x
bằng.
A.
12
. B.
6
. C.
3
. D.
27
.
Câu 17. Trong không gian
Oxyz
, điểm nào dưới đây thuộc đường thẳng
123
:2 14
xy z−−−
∆==
−
?
A.
( )
1; 2; 3P
. B.
( )
2;1; 4N−−
. C.
( )
1; 2; 3M−− −
. D.
( )
2; 1; 4Q−
.
Câu 18. Trong không gian
Oxyz
, mặt phẳng
( )
:3 4 1 0Pxz− +=
có một vectơ pháp tuyến là
A.
( )
3; 4;0n= −
. B.
( )
3; 4;1n= −
. C.
( )
3;0; 4n= −
. D.
( )
3;4;1n=
.
Câu 19. Họ nguyên hàm của hàm số
( )
89
fx x x= +
là
A.
89
xxC++
. B.
9 10
11
9 10
x xC++
C.
78
89x xC++
D.
9 10
xx C++
Câu 20. Họ nguyên hàm của hàm số
( )
2
1
cos
fx x
=
là
A.
tan xC+
. B.
cot xC−+
. C.
tan xC−+
. D.
cot xC+
.
Câu 21. Cho
( )
23
2
1
1d= +
∫
Ixxx
. Đặt
2
1tx= +
, mệnh đề nào dưới đây đúng?
A.
5
3
2
1d.
2
=∫
I tt
B.
5
3
2
d.=∫
I tt
C.
2
3
1
1td.
2
=
∫
It
D.
5
3
2
2 d.=∫
I tt
Câu 22. Cho hàm số bậc ba
( )
=y fx
. Gọi
S
là diện tích hình phẳng giới hạn bởi các đường
( )
, 0, 1= = = −y fx y x
và
2=x
.
3/5 - Mã đề 101
Mệnh đề nào dưới đây đúng?
A.
( ) ( )
12
11
S f x dx f x dx
−
= +
∫∫
. B.
( ) ( )
12
11
S f x dx f x dx
−
=−+
∫∫
.
C.
( ) ( )
12
11
S f x dx f x dx
−
= −
∫∫
. D.
( ) ( )
12
11
S f x dx f x dx
−
=−−
∫∫
.
Câu 23. Gọi
12
,zz
là hai nghiệm phức của phương trình
2
4 50zz− +=
. Gái trị của
22
12
zz+
bằng
A.
. B.
6
. C.
8
. D.
26
.
Câu 24. Họ nguyên hàm của hàm số
( )
5x
fx e
−
=
là:
A.
51x
eC
++
. B.
5x
eC
−+
. C.
5
1
5
x
eC
−+
. D.
5
1
5
x
eC
−
−+
.
Câu 25. Biết
( )
3
2
4=
∫
f x dx
và
( )
3
2
1=
∫g x dx
. Khi đó:
( ) ( )
3
2
−


∫f x g x dx
bằng:
A.
4
. B.
5
. C.
3−
. D.
3
.
Câu 26. Trong không gian
Oxyz
, cho điểm
( )
2; 1;4M−
và mặt phẳng
( )
:3 2 1 0P x yz− ++=
. Phương
trình của mặt phẳng đi qua
M
và song song với mặt phẳng
( )
P
là
A.
2 2 4 21 0xyz−+−=
. B.
2 2 4 21 0xyz−++=
C.
3 2 12 0x yz− +− =
. D.
3 2 12 0x yz− ++ =
.
Câu 27. Họ nguyên hàm của hàm số
( )
sin 6fx x=
là:
A.
1cos 6
6xC+
. B.
1cos 6
6xC−+
. C.
cos 6xC−+
. D.
cos 6xC+
.
Câu 28. Trong không gian Oxyz, cho các vectơ
( )
2;0; 1a= −
và
( )
0; 4;2b= −
. Giá trị của
( )
cos ,ab
bằng
A.
1
5
. B.
1
5
−
. C.
1
5
−
. D.
1
5
.
Câu 29. Trong không gian
Oxyz
, cho hai điểm
( )
0;1; 2A−
và
( )
3; 1; 1B−
. Điểm
( )
;;M abc
thỏa mãn
50+=
 
AM MB
. Khi đó
3++a bc
bằng
A.
9
2
. B.
8
. C.
4
. D.
1
.
Câu 30. Trong không gian
Oxyz
, cho mặt phẳng
( )
: 6 4 90Pxyz− + −=
. Điểm nào dưới đây thuộc mặt
phẳng
( )
P
?
A.
( )
1; 0; 2Q
. B.
( )
1; 0;1N
. C.
( )
1; 0; 3M
. D.
( )
1; 0; 4P
.
Câu 31. Cho số phức
12zi= +
. Phần ảo của số phức
25= +wzz
bằng
A.
7−
. B.
7
. C.
6
. D.
6−
.
Câu 32. Diện tích hình phẳng giới hạn bởi đồ thị của hàm số
223=−+ −yx x
và đường thẳng
3=−−yx
bằng
4/5 - Mã đề 101
A.
11
2
B.
9
2
. C.
7
2
. D.
5
.
Câu 33. Cho số phức
z
thỏa mãn
65iz i= +
. Số phức liên hợp của
z
là:
A.
56= +zi
. B.
56=−−zi
. C.
56=−+zi
. D.
56= −zi
.
Câu 34. Trong không gian
Oxyz
, cho điểm
( )
2; 1; 2M−
và mặt phẳng
( )
:3 2 1 0P x yz+ −+=
. Đường thẳng
đi qua
M
và vuông góc với
( )
P
có phương trình là:
A.
212
321
x yz+ +−
= =
. B.
212
32 1
x yz− −+
= = −
.
C.
212
321
x yz− −+
= =
. D.
212
32 1
x yz+ +−
= = −
.
Câu 35. Cho hai số phức
1
2zi=−+
và
2
1zi= +
. Trên mặt phẳng tọa độ
Oxy
, điểm biểu diễn số phức
12
2zz+
có tọa độ là
A.
( )
3; 3−
. B.
( )
3; 3−
. C.
( )
3; 2−
. D.
( )
2; 3−
.
Câu 36. Cho hai số phức
42= +zi
và
1= +wi
. Môđun của số phức
.zw
bằng
A.
2 10
. B.
2
. C.
25
. D.
40
.
Câu 37. Trong không gian
Oxyz
, cho hai điểm
( )
0;0;1A
và
( )
1; 2; 3B
. Mặt phẳng đi qua
A
và vuông góc
AB
có phương trình là
A.
2 4 40xyz+ + −=
. B.
2 4 17 0xyz++−=
. C.
2 2 11 0xyz+ +−=
. D.
2 2 20xyz+ + −=
.
Câu 38. Tìm hai số thực
x
và
y
thỏa mãn
( ) ( )
3 42 5 2x yi i x i++−=+
với
i
là đơn vị ảo.
A.
2x=
;
0y=
B.
2x= −
;
0y=
C.
2x= −
;
4y=
D.
2x=
;
4y=
Câu 39. Trong không gian
Oxyz
, cho hai điểm
( )
1;3; 2A−
,
( )
3; 1; 4B−
. Mặt cầu đường kính
AB
có
phương trình
A.
( ) ( ) ( )
2 22
2 1 1 14x yz+ ++ ++ =
. B.
( ) ( ) ( )
2 22
2 1 1 56− +− +− =x yz
.
C.
( ) ( ) ( )
2 22
2 1 1 14x yz− +− +− =
. D.
( ) ( ) ( )
2 22
2 1 1 14− +− +− =x yz
.
Câu 40. Xét hàm số
()fx
liên tục trên
và
( )
( )
2
3
0
83 4d2+ =
∫fx x x
. Khi đó
( )
2
0
d
∫
fx x
bằng
A.
3
. B.
4
. C.
2
. D.
1
.
PHẦN II. TỰ LUẬN (2 điểm)
Câu 1. Cho số phức
z
thỏa
( ) ( )
4 3 4 48iz z i i++ −=−
. Tính mô-đun của số phức
2zi+
.
Câu 2. Cho hàm số
( )
fx
liên tục trên
và thỏa mãn
( )
7
1
d6fx x=
∫
.
Tính tích phân
( )
2
3
0
4 3 3 1dI x fx x

=++

∫
.
Câu 3. Tìm tất cả giá trị thực của tham số
m
sao cho có đúng
3
số số phức
z
thỏa mãn
1−+ =z im
và
2
4+
z
z
là số thực.
Câu 4. Trong không gian
Oxyz
, cho hai điểm
( ) ( )
2;0;0 ; 1;3; 3−−AB
và đường thẳng
2
:11 1
−
∆==
xyz
Gọi
(;;)M abc
là điểm thuộc đường thẳng
∆
sao cho chu vi tam giác
MAB
nhỏ nhất. Khi đó
++abc
bằng.
5/5 - Mã đề 101
------ HẾT ------
Thí sinh không được sử dụng tài liệu, giám thị coi thi không giải thích gì thêm.
Họ và tên học sinh :..................................................... Số báo danh : ...................