Trang 1/6 - Mã đề: 149
S
Ở GD & ĐT
THANH HÓA
TRƯỜNG THPT CHUYÊN LAM SƠN
ĐỀ THI CHÍNH THỨC
( Đề thi có 06 trang)
ĐỀ KIỂM TRA KSCL GIỮA HỌC KÌ II, KHỐI 12
NĂM HỌC 2019 - 2020
Môn thi: Toán.
Ngày thi: 16/05/2020
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Họ và tên thí sinh:..............................................................................Số báo danh:.................................
Mã
đ
ề: 149
Câu 1. Nếu
1 1
0 0
( )dx 2, ( )dx 5
f x g x thì
1
0
( ) 2 ( ) dx
f x g x bằng
A.
1
. B.
9
. C.
12
. D.
8
.
Câu 2. Cho khối cầu có bán kính
2.
R
Thể tích khối cầu đã cho bằng
A.
4
. B.
16
. C.
32
. D.
32
3
.
Câu 3. Tập nghiệm
S
của bất phương trình
2 2
log 2 1 log
x x
là
A.

0;S. B.

1;S. C.
0;1
S. D.

1;
2
S.
Câu 4. Gọi
, ,
l h r
lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình nón. Diện tích xung quanh
xq
S
của hình nón là
A. 1
2
xq
S rl
. B.
xq
S rh
. C.
xq
S rl
. D.
2
1
3
xq
S r h
.
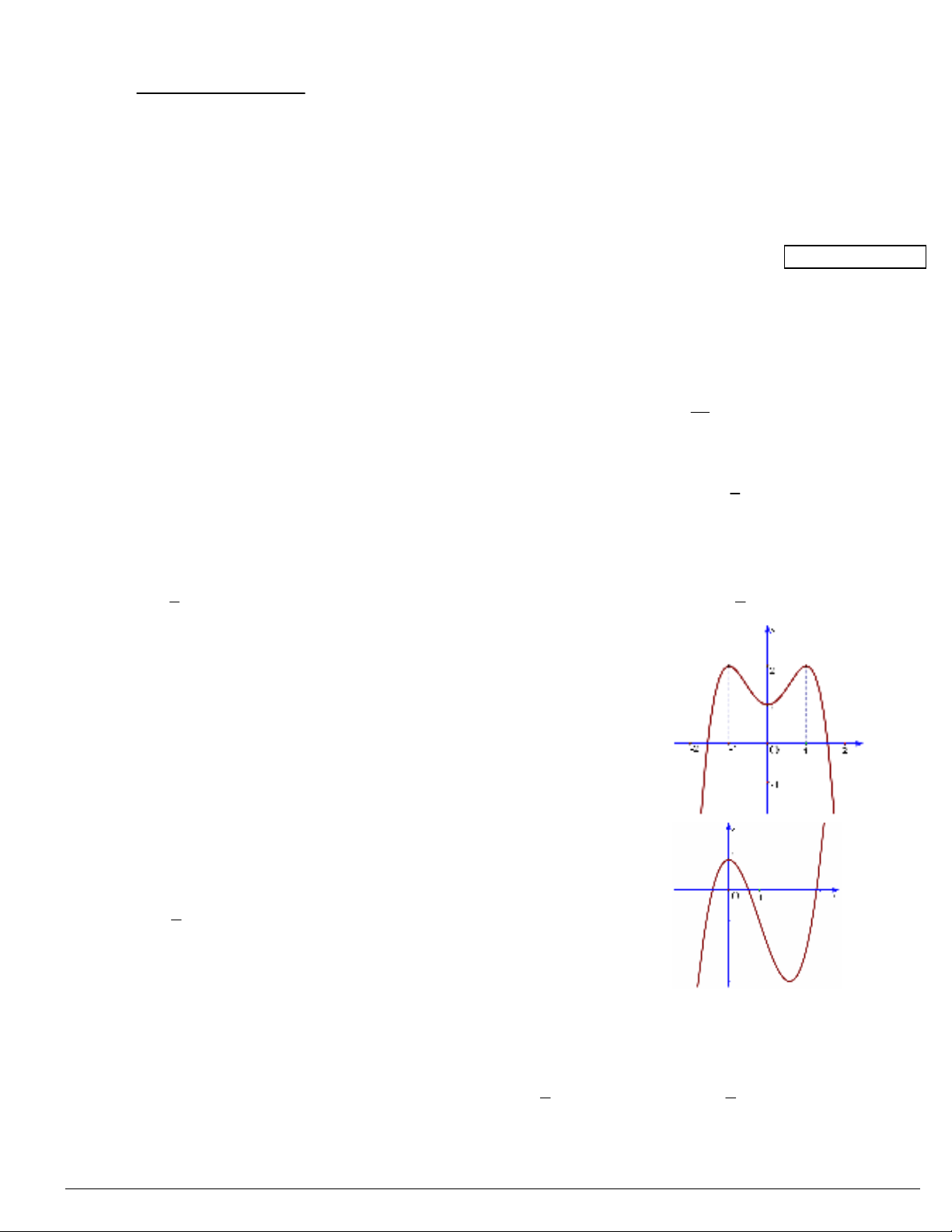
Câu 5. Cho hàm số 4 2
y ax bx c
(với
, ,
a b c
), có đồ thị như hình vẽ
bên. Số điểm cực trị của hàm số đã cho là
A.
0
. B.
3
.
C.
2
. D.
1
.
Câu 6. Đường cong trong hình vẽ bên là đồ thị của một trong bốn hàm số
được liệt kê ở bốn phương án dưới đây. Hỏi đó là hàm số nào?
A.
2
3 2 1
y x x
. B. 3 2
3 1
y x x
.
C. 3 2
1
1
3
y x x
. D. 4 2
3 1
y x x
.
Câu 7. Thể tích của khối chóp có đáy là hình vuông cạnh
2
a
và chiều cao của khối chóp bằng
3
a
là
A.
3
V a
. B.
3
3
V a
. C.
3
4
V a
. D.
3
12
V a
.
Câu 8. Thể tích của khối nón có chiều cao
h
và bán kính đáy
r
là
A.
2
V r h
. B.
V rh
. C.
2
1
3
V r h
. D.
2
1
3
V rh
.
Câu 9. Cho cấp số nhân
n
u
với
1 2
3, 6
u u . Công bội của cấp số nhân đã cho bằng
A.
2.
B.
3
. C.
18
. D.
3
.
Trang 2/6 - Mã đề: 149
Câu 10. Trong không gian
Oxyz
cho đường thẳng 1 2
:
1 3 2
x y z
d
. Véc tơ nào trong các véc tơ dưới đây
là một véc tơ chỉ phương của
d
?
A.
1;2; 0
u. B.
1; 3;2
u
. C.
1; 3; 2
u
. D.
1; 3; 2
u
.
Câu 11. Số phức liên hợp của số phức
1 2
z i
là
A.
1 2
z i
. B.
1 2
z i
. C.
1 2
z i
. D.
2
z i
.
Câu 12. Cho hai số thực dương tùy ý
a
và
b
với
1.
a
Khi đó
loga
ab
bằng
A.
log
a
a
b
. B.
1 log
a
b
. C.
log
a
a b
. D.
log
a
a b
.
Câu 13. Nghiệm của phương trình 5
log (2 1) 2
x
là
A.
12
x
. B.
31
2
x. C.
24
x
. D.
9
2
x.
Câu 14. Họ nguyên hàm của hàm số
2
3 sin
f x x x
là
A.
3
cos
x x C
. B.
6 cos
x x C
. C.
3
x C
. D.
3
sin
x x C
.
Câu 15. Diện tích xung quanh của hình trụ có độ đài đường sinh
3
l
và bán kính đáy
4
r
là
A.
24
. B.
16
. C.
4
. D.
12
.
Câu 16. Hàm số 2
2
x x
y
có đạo hàm là
A.
' 2 1
y x
. B.
2
' 2 1 2 . ln 2
x x
y x
. C. 2
' 2 . ln 2
x x
y
. D.
2
' 2 1 2
x x
y x
.
Câu 17. Cho hàm số
y f x
có bảng biến thiên như hình vẽ
Hàm số
y f x
đồng biến trên khoảng nào dưới đây?
A.
0;1
. B.
; 1

. C.
2; 3
. D.
1; 0
.
Câu 18. Cho số phức
(1 2 ).
z i i
Tìm điểm biểu diễn của số phức đó trên mặt phẳng tọa độ.
A.
( 2;1)
M
. B.
(1; 2)
M
. C.
(1;2)
M
. D.
(2;1)
M
.
Câu 19. Có bao nhiêu cách chọn ba học sinh từ một nhóm gồm
15
học sinh ?
A.
3
15
. B.
15
3
. C.
3
15
A
. D.
3
15
C
.
Câu 20. Cho hai số phức
1
2 ,
z i
2
1 3
z i
. Môdun của số phức
1 2
2
z z
bằng
A.
50
. B.
65
. C.
26
. D.
41
.
Câu 21. Trong không gian
,
Oxyz
cho mặt cầu
2 2 2
: ( 1) ( 3) ( 5) 3.
S x y z Tâm của
S
có tọa độ là
A.
1; 3; 5
. B.
1; 3; 5
. C.
1; 3; 5
. D.
1; 3; 5
.
Câu 22. Cho hàm số
y f x
có bảng biến thiên như sau
Trang 3/6 - Mã đề: 149
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A.
4
. B.
1
. C.
3
. D.
2
.
Câu 23. Cho hàm số bậc ba
y f x
có đồ thị như hình vẽ bên. Số nghiệm
thực của phương trình
2 3 0
f x
là
A.
2
. B.
0
.
C.
3
. D.
1
.
Câu 24. Trong không gian
Oxyz
, tọa độ điểm
H
là hình chiếu vuông góc của điểm
2;1; 1
A
lên trục
Oy
là
A.
2; 0; 1
H
. B.
0;1; 1
H
. C.
0;1; 0
H. D.
2; 0; 0
H.
Câu 25. Trong không gian
,
Oxyz
cho mặt phẳng
: 5 3 0
P x y z . Véc tơ nào trong các véc tơ dưới đây
là một véc tơ pháp tuyến của
P
?
A.
5;1; 1
n. B.
1; 1; 3
n. C.
5; 1; 3
n. D.
5;1; 3
n.
Câu 26. Diện tích phần hình phẳng tô đậm trong hình vẽ bên được tính theo
công thức nào dưới đây?
A.
2
1
2 2
x dx
. B.
2
2
1
2 2 4
x x dx
.
C.
2
2
1
2 2 4
x x dx
. D.
2
1
2 2
x dx
.
Câu 27. Cho hàm số
f x
có đạo hàm là
2 3
' 1 2 3 ,f x x x x x x . Số điểm cực trị của hàm số
f x
là
A.
3
. B.
1
. C.
2
. D.
4
.
Câu 28. Tập nghiệm của bất phương trình
2
2 7 5
2 1
x x là
A.
1
; 5
2. B.
5
1;
2
. C.

1
; 5;
2. D.

5
;1 ;
2.
Câu 29. Giá trị nhỏ nhất của hàm số
3
3 5
f x x x

trên đoạn
2; 4
là
A.
5
. B.
0
. C.
7
. D.
3
.
Câu 30. Trong không gian
Oxyz
cho mặt phẳng
: 2 2 2 1 0.
P x y z Phương trình tham số của đường
thẳng đi qua điểm
3; 0;1
I
và vuông góc với
P
là
A.
3 2
2
1
x t
y t
z t
. B.
3
1
x t
y t
z t
. C.
3
1
x t
y t
z t
. D.
3 2
2
1
x t
y t
z t
.
Câu 31. Gọi
1 2
,
z z
là hai nghiệm phức của phương trình 2
2 3 4 0
z z
. Xét
1 2
1 2
1 1
iz z
z z
 , viết số phức
dưới dạng
x yi
,x y
.
A. 3
2
2
i
. B. 3
2
4
i
. C.
3
2
2
i
. D. 3
2
4
i
.
Trang 4/6 - Mã đề: 149
Câu 32. Cho lăng trụ đứng
. ' ' '
ABC A B C
có
' 2
AA a
. Tam giác
ABC
vuông tại
A
và
2 3
BC a
. Tính thể tích hình trụ ngoại tiếp hình lăng trụ đã
cho (tham khảo hình vẽ).
A.
3
2
a
. B.
3
a
.
C.
3
6
a
. D.
3
4
a
.
Câu 33. Viện Hải dương học dự định làm một bể cá bằng kính
phục vụ khách tham quan, biết rằng mặt cắt dành cho lối đi là
nửa đường tròn (kích thước như hình vẽ). Tính diện tích kính
để làm mái vòm của bể cá.
A.
2
200
m
. B.
2
100
m
.
C.
2
200
m
. D.
2
100
m
.
Câu 34. Cho hàm số
3 2
( , , , )
y ax bx cx d a b c d có đồ thị như hình
vẽ bên. Trong các số
,,,
a b c d
có bao nhiêu số dương ?
A.
1
. B.
2
.
C.
3
. D.
4
.
Câu 35. Cho hai số phức
1 2
2 5 , 3 4
z i z i
. Phần ảo của số phức
1 2
z z
bằng
A.
7
i
. B.
23
i
. C.
23
. D.
7
.
Câu 36. Cho hình chóp
.
S ABCD
có
SA
vuông góc với mặt phẳng đáy,
,
SA a
ABCD
là hình chữ nhật và
, 2
AB a AD a
. Góc giữa đường
thẳng
SC
và mặt phẳng
ABCD
là
A.
o
60
. B.
o
45
.
C.
o
90
. D.
o
30
.
Câu 37. Số giao điểm của đồ thị hàm số
3
3
y x
và đồ thị hàm số
3 1
y x
là
A.
2
. B.
3
. C.
1
. D.
0
.
Câu 38. Trong không gian
Oxyz
cho hai điểm
2;0;1
A,
4;2;5
B, phương trình mặt phẳng trung trực của đoạn
thẳng
AB
là
A.
3 2 10 0
x y z
. B.
3 2 10 0
x y z
.
C.
3 2 10 0
x y z
.
D.
3 2 10 0
x y z
.
Trang 5/6 - Mã đề: 149
Câu 39. Cho hàm số
y f x
, hàm số
'
y f x
liên tục trên
và có đồ thị
như hình vẽ bên. Bất phương trình
22
f x x x m

(
m
là tham số thực)
nghiệm đúng với mọi
1;2
x
khi và chỉ khi
A.
2 2
m f
. B.
1 1
m f
. C.
1 1
m f
. D.
2
m f
.
Câu 40. Cho
f x
và
g x
là hai hàm số liên tục và có một nguyên hàm lần lượt là
2019
F x x
,
2
2020
G x x
. Tìm một nguyên hàm
H x
của hàm số
.
h x f x g x
, biết
1 3
H
.
A.
3
3
H x x
. B.
2
5
H x x
. C.
3
H x x
. D.
2
2
H x x
.
Câu 41. Đầu năm 2019, ông A mở một công ty và dự kiến tiền lương trả cho nhân viên là
600
triệu đồng cho
năm này. Ông A dự tính số tiền trả lương sẽ tăng
15%
mỗi năm. Hỏi năm đầu tiên số tiền lương ông A phải trả
cho năm đó vượt quá 1 tỉ đồng là năm nào ?
A. 2024. B. 2026. C. 2025. D. 2023.
Câu 42. Cho hàm số
f x
liên tục trên đoạn
0;10
thỏa mãn
10 10
0 2
dx 7, dx 1
f x f x . Tính
1
0
2 dx
P f x
A.
6
P
. B.
6
P
. C.
3
P
. D.
12
P
.
Câu 43. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thoi cạnh
a
. Tam
giác
ABC
là tam giác đều, hình chiếu vuông góc của đỉnh
S
trên mặt
phẳng
ABCD
trùng với trọng tâm của tam giác
ABC
. Góc giữa đường
thẳng
SD
và mặt phẳng
ABCD
bằng
0
30
. Tính khoảng cách từ
B
đến
mặt phẳng
SCD
theo
a
.
A.
21
7
a. B.
3
a
. C.
a
. D.
2 21
3
a.
Câu 44. Giải bóng chuyền VTV Cup có
12
đội tham gia trong đó có
9
đội nước ngoài và
3
đội của Việt Nam.
Ban tổ chức cho bốc thăm ngẫu nhiên để chia thành
3
bảng đấu
A
,
B
,
C
mỗi bảng
4
đội. Xác suất để
3
đội Việt
Nam nằm ở
3
bảng gần nhất với số nào trong các số sau đây?
A.
11
25
. B.
3
20
. C.
39
100
. D.
29
100
.
Câu 45. Cho các số thực
a
,
b
thỏa mãn
1
a b
và 1 1
2020
log log
b a
a b
. Giá trị biểu thức
1 1
log log
ab ab
P
b a
bằng
A.
2014
. B.
2016
. C.
2018
. D.
2020
.
Câu 46. Cho hàm số
( )
y f x
có đạo hàm liên tục trên
, bảng biến thiên của hàm số
'( )
f x
như sau