_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Đỗ Văn Đức 1
1. Mỗi mặt của hình bát diện đều là
A. Hình vuông. B. Tam giác đều. C. Bát giác đều. D. Ngũ giác đều.
2. Trong không gian
,
Oxyz
cho
2 3 4 .
u j i k
Tọa độ của vectơ
u
là
A.
3; 2;4 .
B.
3;2; 4 .
C.
2; 3; 4 .
D.
3;2;4 .
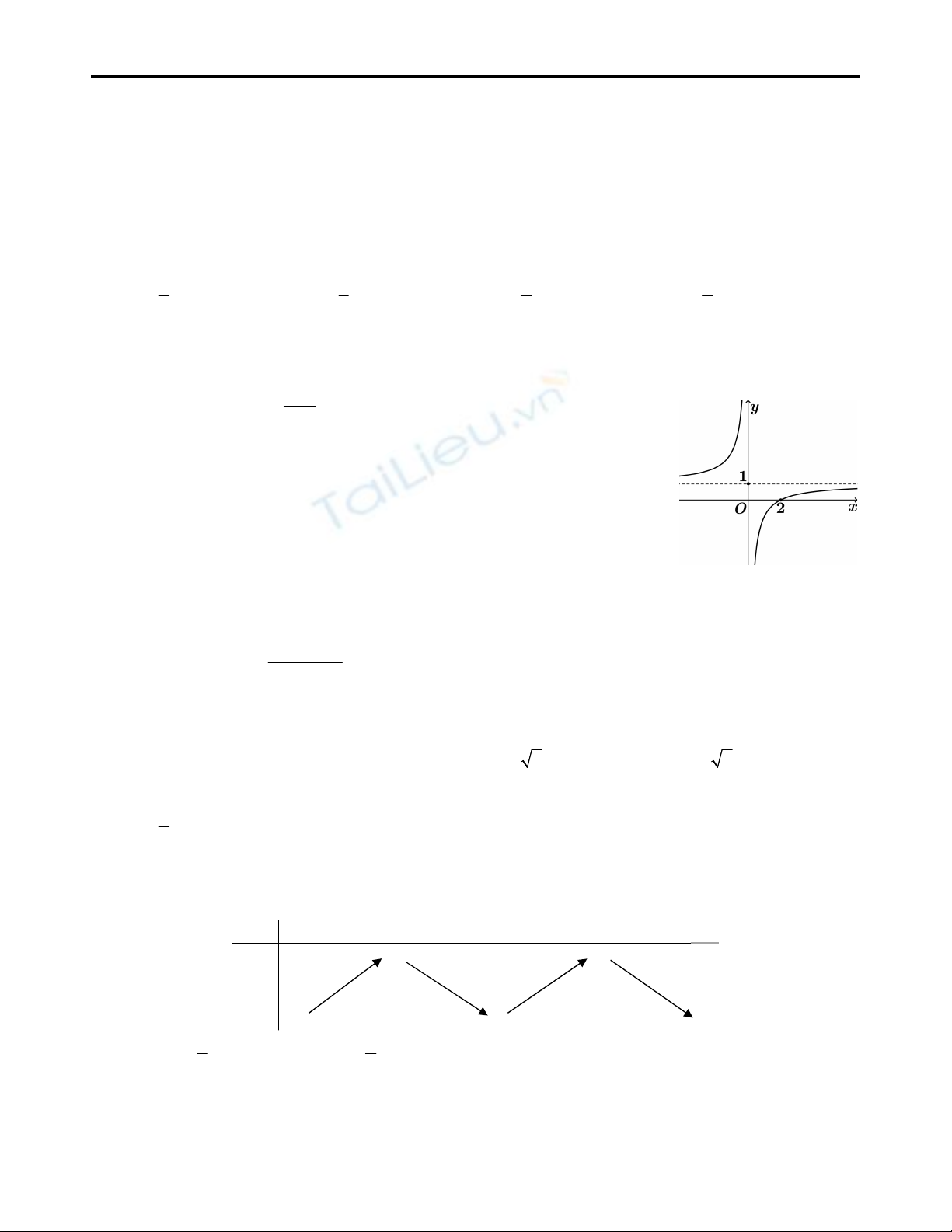
3. Cho hàm số
y f x
liên tục trên
3;3
và có bảng xét dấu đạo hàm như hình vẽ. Hàm số đã cho có
bao nhiêu điểm cực trị thuộc khoảng
3;3 ?
x
3
1
0
1
2
3
f x
0
0
0
0
A. 2. B. 3. C. 1. D.
4.
4. Thể tích của khối chóp .
O ABC
có , ,
OA OB OC
đôi một vuông góc bằng
A. 1
. . .
6
OAOB OC
B. 1
. . .
2
OAOB OC
C. 1
. . .
3
OAOB OC
D.
. . .
OAOB OC
5. Khối nón có bán kính đáy, đường cao, đường sinh lần lượt là
, ,
r h l
thì có thể tích bằng
A.
.
rl
B. 2
.
r h
C.
2 2
1
.
3
l h h
D.
2
1
.
3
r l
6. Giả sử
,
a b
và
là các số thực tùy ý
0, 0 .
a b Mệnh đề nào sau đây đúng?
A.
.
ab a b
B.
.
a b a b
C.
.
ab a b
D.
1
.
a
a b
b
7. Trong không gian
,
Oxyz
khoảng cách từ điểm
1; 2;3
M đến gốc tọa độ bằng
A. 2. B. 3. C.
1.
D.
14.
8. Phương trình
log 1 2
x
có nghiệm là
A. 101. B. 9. C. 99. D. 11.
9. Khối lăng trụ có 8 đỉnh thì có bao nhiêu mặt?
A.
8.
B.
4.
C.
6.
D.
10.
10. Tiệm cận đứng của đồ thị hàm số
2 2
1
x
y
x
là
A.
1.
y
B.
1.
x
C.
1.
x
D.
2.
y
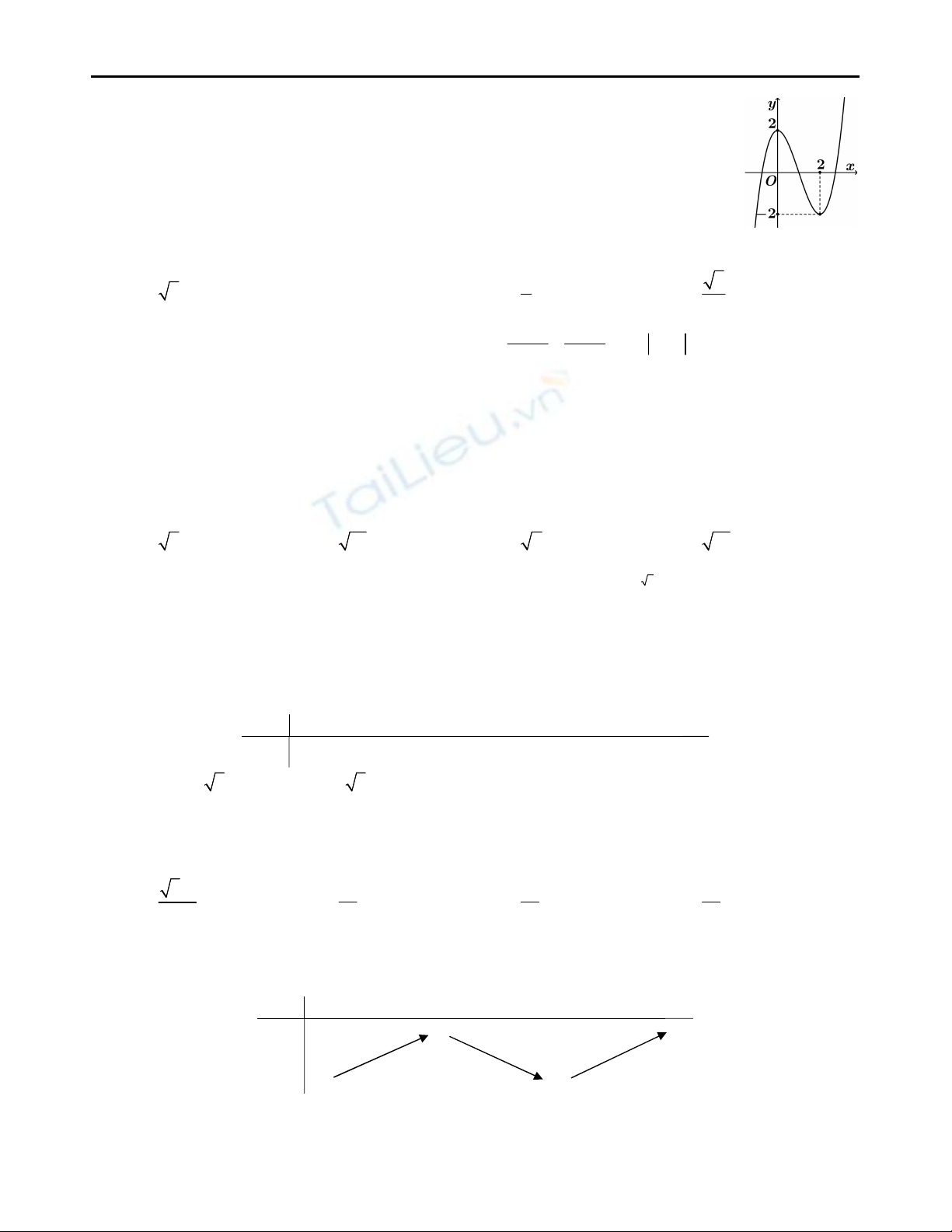
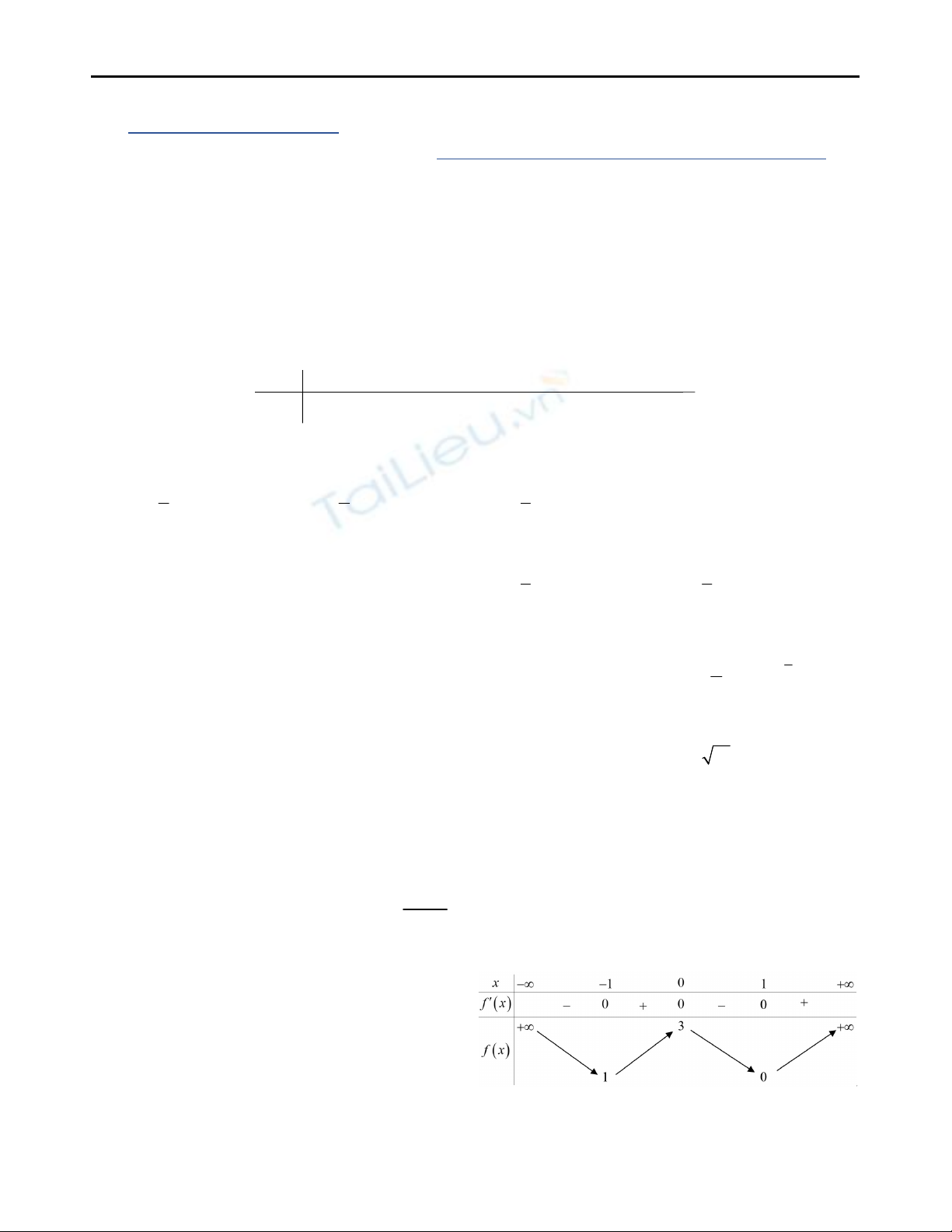
11. Cho hàm số
y f x
liên tục trên
và có
bảng biến thiên như hình bên. Phương trình
2 0
f x
có bao nhiêu nghiệm?
A. 2. B. 3.
C. 1. D. 4.
TRƯỜNG ĐẠI HỌC VINH
TRƯỜNG THPT CHUYÊN
ĐỀ THI KSCL HỌC KỲ I NĂM HỌC 2020 - 2021
Bài thi: TOÁN - Lớp: 12
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Đỗ Văn Đức 2
12. Biết rằng đường cong ở hình bên là đồ thị của một trong các hàm số dưới đây,
đó là hàm số nào?
A.
3 2
2 .
y x x
B. 3 2
5 6 .
y x x x
C. 3 2
5 6 .
y x x x
D.
3 2
2 .
y x x
13. Diện tích của mặt cầu có đường kính
AB a
là
A.
2
.
a
B.
2
4 .
a
C.
2
4
.
3
a
D.
2
1
.
6
a
14. Giả sử
,
a b
là các số thực dương tùy ý thỏa mãn
2 3 4
4 .
a b
Mệnh đề nào sau đây đúng?
A. 2 2
2log 3log 4.
a b
B. 2 2
2log 3log 8.
a b
C. 2 2
2log 3log 8.
a b
D. 2 2
2log 3log 4.
a b
15. Cho hàm số
y f x
có đồ thị như hình bên. Hàm số đã cho đồng biến
trên khoảng
A.
0;1 .
B.
2; 1 .
C.
1;0 .
D.
1;2 .
16. Tập nghiệm của bất phương trình 2
3 9
x
là
A.
;1 .
 B.
;0 .
 C.
1; .
D.
0; .

17. Cho hình chóp .
S ABCD
có đáy
ABCD
là hình vuông cạnh
,
a
SA
vuông góc với
.
ABCD
Góc
giữa
SB
và
ABCD
bằng
45 .
Thể tích của khối chóp .
S ABCD
bằng
A.
3
1
.
3
a
B.
3
2 .
a
C.
3
2
.
3
a
D.
3
.
a
18. Đạo hàm của hàm số
3 1
3 1
x
x
f x
là
A.
2
2
.3 .
3 1
x
x
f x
B.
2
2
.3 .
3 1
x
x
f x
C.
2
2
.3 ln 3.
3 1
x
x
f x
D.
2
2
.3 ln 3.
3 1
x
x
f x
19. Cho hàm số
y f x
có đạo hàm trên
là
2 3
3 4 .
f x x x x x
Hàm số đã cho có điểm cực
đại là
A.
2.
x
B.
0.
x
C.
3.
x
D.
2.
x
20. Cho hàm số
y f x
có đạo hàm
2 2
1 , .
f x x x x
Hàm số
y f x
đồng biến trên
khoảng?
A.
2; .
B.
0;2 .
C.
; 1 .

D.
1;1 .
21. Có bao nhiêu cặp số thực dương
;
a b
thỏa mãn 2
log
a
là số nguyên dương,
2 4
log 1 log
a b
và
2 2 21
2 ?
a b
A. 6. B. 5. C. 8. D. 7.
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Đỗ Văn Đức 3
22. Biết rằng
,
là các số thực thỏa mãn
2 2 2 8 2 2 .
Giá trị của
2
bằng
A. 3. B. 2. C. 1. D. 4.
23. Gọi
,
m M
lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của hàm số
2
4 sin
f x x x
trên đoạn
1;2 .
Giá trị của
m M
bằng
A.
4.
B.
2.
C.
0.
D.
4.
24. Cho khối lăng trụ tam giác .
ABC A B C
có thể tích
.
V
Thể tích của khối chóp .
B ACC A
bằng
A.
2
.
3
V
B.
1
.
3
V
C.
1
.
2
V
D.
3
.
4
V
25. Biết rằng phương trình 2
2 2
log 7log 9 0
x x
có hai nghiệm
1 2
, .
x x
Giá trị
1 2
x x
bằng
A. 128. B. 9. C. 64. D.
512.
26. Cho hàm số
1
.
1
x
f x
x
Biết rằng đường cong ở hình bên là đồ thị của
một trong các hàm số dưới đây, đó là hàm số nào?
A.
1 .
y f x
B.
1 .
y f x
C.
1 .
y f x
D.
1 .
y f x
27. Cho hình chóp .
S ABC
có đáy
ABC
là tam giác vuông tại
,
B
SA
vuông
góc với
.
ABC
Tâm của mặt cầu ngoại tiếp hình chóp .
S ABC
là
A. Trung điểm của
.
SA
B. Trung điểm của
.
SC
C. Trung điểm của
.
SB
D. Trung điểm của
.
AC
28. Đồ thị hàm số
3
3
4
3 2
x x
y
x x
có bao nhiêu đường tiệm cận?
A. 4. B. 1. C. 2. D.
3.
29. Thể tích của khối lăng trụ tứ giác đều .
ABCD A B C D
có
2
AC AA a
là
A.
3
4 .
a
B.
3
2 .
a
C.
3
2 .
a
D.
3
2 2 .
a
30. Diện tích xung quanh của hình trụ có thiết diện qua trục là hình vuông cạnh
a
bằng
A.
2
3
.
2
a
B.
2
2 .
a
C.
2
3 .
a
D.
2
.
a
31. Cho hàm số
y f x
có đạo hàm trên
và có bảng biến thiên như hình vẽ bên. Hàm số
1 2
y f x
đạt cực tiểu tại
x

1
0
2

f x
1
2
1
A.
1
.
2
x
B.
1
.
2
x
C.
1.
x
D.
0.
x
32. Trong không gian
,
Oxyz
góc giữa hai vectơ
1;1;2
u
và
1; 2; 1
v
bằng
A.
150 .
B.
60 .
C.
30 .
D.
120 .
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Đỗ Văn Đức 4
33. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Hàm số
3 2
y f x
nghịch
biến trên khoảng
A.
2;4 .
B.
0;3 .
C.
;1 .
 D.
3; .
34. Cho hình hộp chữ nhật .
ABCD A B C D
có
1, 2.
AB AD AA
Bán kính mặt cầu
ngoại tiếp tứ diện
AB CD
bằng
A.
5.
B.
3.
C.
3
.
2
D.
5
.
2
35. Hỏi có bao nhiêu số nguyên âm
a
để phương trình 1 1 4
9 3 3 9
x x
x x a
có hai nghiệm thực
phân biệt?
A. Vô số. B. 5. C. 7. D. 4.
36. Trong không gian Oxyz, cho các điểm
1;3;1 , 1;1;1 .
A B Đường thẳng
AB
cắt mặt phẳng
Oyz
tại điểm
.
M
Độ dài của
OM
bằng
A.
5.
B.
13.
C.
2.
D.
10.
37. Hỏi có bao nhiêu số nguyên dương
m
để bất phương trình
2
22
log log 32
x x m
nghiệm đúng với
mọi
0;2 ?
x
A. 8. B. 9. C. 12. D. 13.
38. Cho hàm số
f x
có bảng xét dấu đạo hàm như hình bên. Hàm số
2
1
y f x
nghịch biến trên
khoảng
x

3
2
0
1
3

f x
0
0
0
0
0
A.
2; 3 .
B.
3;2 .
C.
2; .
D.
1;1 .
39. Cho hình chóp .
S ABC
có đáy
ABC
là tam giác cân tại
,
A
,
AB a
120 ,
BAC
tam giác
SAB
đều
và nằm trong mặt phẳng vuông góc với
.
ABC
Thể tích khối chóp .
S ABC
bằng
A.
3
3
.
2
a
B.
3
.
2
a
C.
3
.
8
a
D.
3
.
3
a
40. Cho hàm số
.
y f x
Hàm số
y f x
có bảng biến thiên như hình vẽ bên. Hỏi hàm số
2
g x f x x
có bao nhiêu điểm cực trị?
x

1
1

f x

1
1

A. 1. B. 0. C. 2. D. 3.
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầy Đỗ Văn Đức 5
41. Cho khối trụ
T
có thiết diện qua trục là hình vuông. Mặt cầu
S
có bán kính bằng
2
chứa hai
đường tròn đáy của khối trụ
.
T
Thể tích của
T
bằng
A.
3 .
B.
.
C.
2 .
D.
2 .
42. Cho hình lăng trụ đứng .
ABC A B C
có đáy
ABC
là tam giác vuông tại
,
B
3 ,
AB a
2 ,
AC a
đường thẳng
BC
tạo với mặt phẳng
ACC A
một góc
30 .
Diện tích mặt cầu ngoại tiếp hình lăng
trụ đã cho bằng
A.
2
3 .
a
B.
2
24 .
a
C.
2
4 .
a
D.
2
6 .
a
43. Cho hàm số
.
f x
Hàm số
y f x
có bảng biến thiên như hình vẽ. Tất cả các giá trị của tham số
m để bất phương trình
2 3
1
3
m x f x x
nghiệm đúng với mọi
0;3
x là
x
1
1
3
f x
1
3
2
A.
2
1 .
3
m f
B.
3 .
m fC.
0 .
m fD.
0 .
m f
44. Trong không gian
,
Oxyz
cho
ABC
có
2;1;1 , 1;2;1
A B và
1;1;2 .
C Độ dài đường cao kẻ từ
A
của
ABC
bằng
A.
6
.
2
B.
2.
C.
3
.
2
D.
3.
45. Một nguồn âm đẳng hướng phát ra từ điểm O. Mức cường độ âm tại điểm M cách O một khoảng R
được tính bởi công thức
2
log
M
k
L
R
(Ben), với
0
k
là hằng số. Biết điểm
O
thuộc đoạn thẳng
AB
và mức cường độ âm tại
A
và
B
lần lượt là
4,3
A
L
(Ben) và
5
B
L
(Ben). Mức cường độ âm tại
trung điểm của
AB
bằng (làm tròn đến hai chữ số thập phân)
A.
4,65
(Ben). B.
4,58
(Ben). C.
5,42
(Ben). D.
9,40
(Ben).
46. Cho hàm số bậc ba
y f x
có đồ thị như hình bên. Phương trình
2 1 6 3 1
f x x
có bao nhiêu nghiệm?
A. 4. B. 5.
C. 3. D. 6.
47. Cho hàm số đa thức bậc bốn
.
f x
Đồ thị hàm số
3 2
y f x
được cho
như hình bên. Hàm số
y f x
nghịch biến trên khoảng
A.
; 1 .

B.
1;1 .
C.
1;5 .
D.
5; .