PHÒNG GIÁO D C VÀ ĐÀO T O Đ KI M TRA H C K IỤ Ạ Ề Ể Ọ Ỳ
HUY N ĐÔNG ANHỆ NĂM H C 2018 – 2019Ọ
Môn: TOÁN - L P 9Ớ
Th i gian làm bài: 90 phútờ (không k giaoể
đ)ề
Bài I (1,0 đi m)ể
Th c hi n các phép tính:ự ệ
a) b)
Bài II (2,0 đi m)ể
Gi i các ph ng trình:ả ươ
a)
b)
Bài III (2,5 đi m)ể
Cho bi u th c P = ể ứ
a) Tìm đi u ki n xác đnh và rút g n Pề ệ ị ọ
b) Tìm các giá tr c a x đ P < 0ị ủ ể
c) Tìm m đ x th a mãn: ể ỏ
Bài IV (1,0 đi m)ể
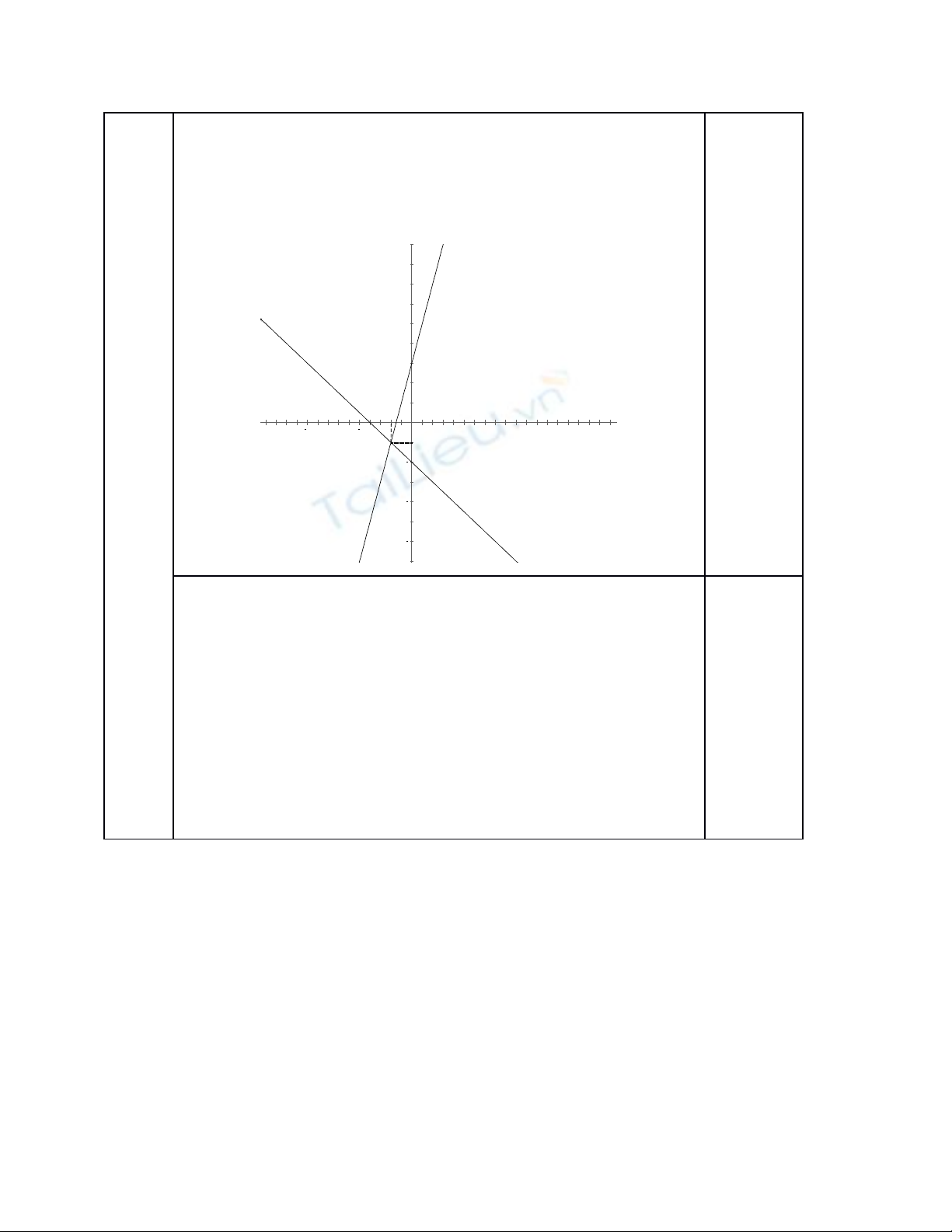
Cho hàm s y = 2x + 3 có đ th là (d) và hàm s y = - 0,5x – 2 có đ th làố ồ ị ố ồ ị
(d’).
a) V (d) và (d’) trên cùng m t m t ph ng t a đẽ ộ ặ ẳ ọ ộ
b) Xác đnh t a đ giao đi m c a hai đ th b ng ph ng pháp đi sị ọ ộ ể ủ ồ ị ằ ươ ạ ố
Bài V (3,5 đi m)ể
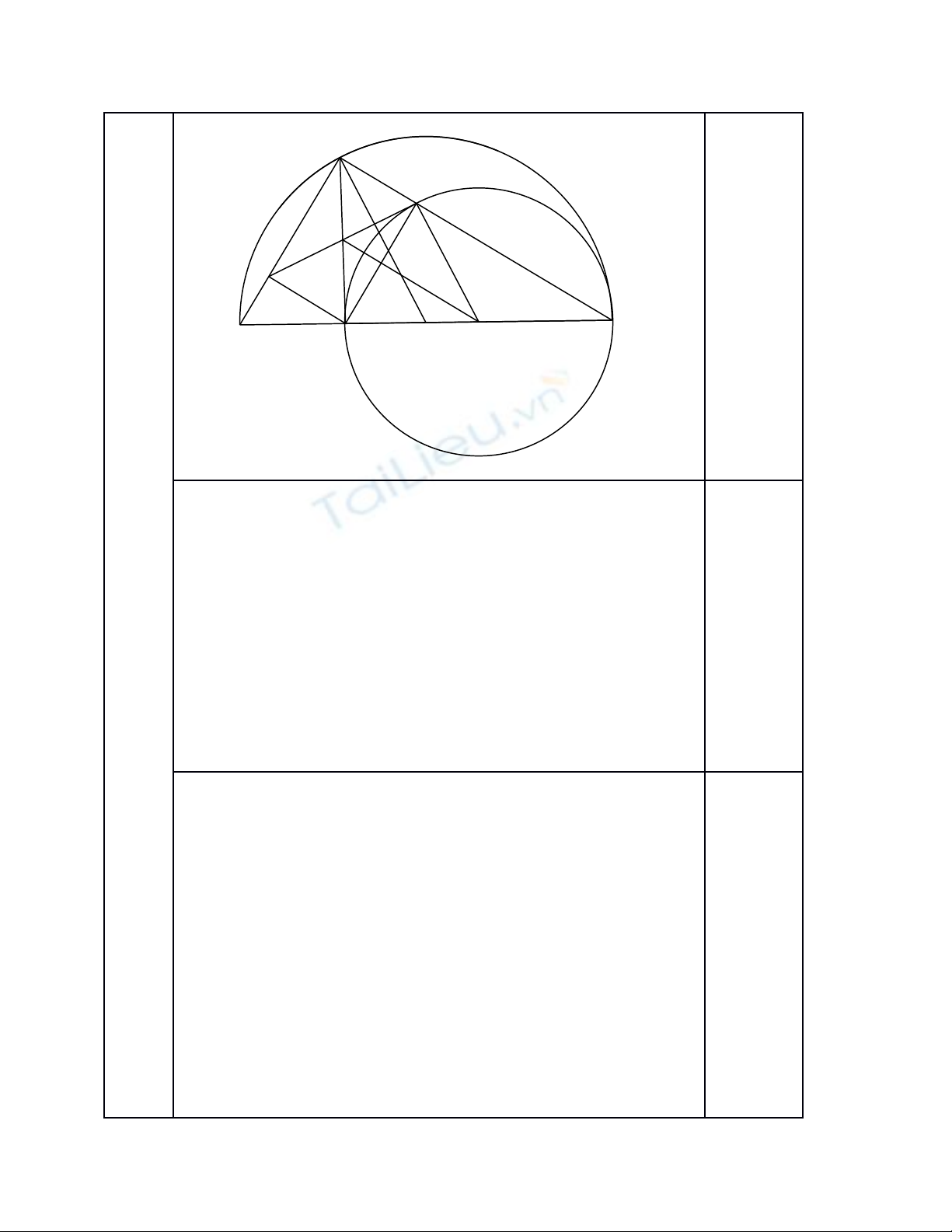
Cho n a đng tròn (O), đng kính AB và đi m C thu c n a đng trònử ườ ườ ể ộ ử ườ
đó. T C k CH vuông góc v i AB (H ừ ẻ ớ ∈ AB). G i M là hình chi u c a H trênọ ế ủ
AC, N là hình chi u c a H trên BC. ế ủ
a) Ch ng minh t giác HMCN là hình ch nh tứ ứ ữ ậ
b) Ch ng minh MN là ti p tuy n c a đng tròn đng kính BHứ ế ế ủ ườ ườ
c) Ch ng minh MN vuông góc v i COứ ớ
d) Xác đnh v trí c a đi m C trên n a đng tròn đng kính AB đ đo nị ị ủ ể ử ườ ườ ể ạ
th ng MN có đ dài l n nh t?ẳ ộ ớ ấ
---------------------------H t------------------------ế
H NG D N CH MƯỚ Ẫ Ấ
Bài N i dungộĐi mể
ITh c hi n phép tínhự ệ
a) 0,5 đi mể
b) 0,5 đi mể
II
Gi i ph ng trìnhả ươ
a)
Đk: x ≥ 0
Ph ng trình có nghi m x = 49ươ ệ
1,0 đi mể
b)
Đk: x ≥ - 1
Ph ng trình có nghi m x = 35ươ ệ 1,0 đi mể
III
Cho bi u th c: ể ứ
a) Rút g n Pọ
P =
ĐKXĐ: … ta có x > 0, x ≠ 1 (*)
P =
P =
P =
P =
1,0 đi mể
b) Tìm các giá tr c a x đ P < 0ị ủ ể
Có P < 0
v i (*)ớ
V y thì P < 0ậ
0,5 đi mể
c) Tìm m đ x th a mãn ể ỏ
Có
v i (*)ớ
Vì x > 0 nên hay
Đ có s x th a mãn thì hay ể ố ỏ
x ≠ 1 nên m ≠ 1
V y m > -1; m ≠ 1 ta có x th a mãn ậ ỏ
1,0 đi mể
IV a) Cho hàm s y = 2x + 3 có đ th là (d) và hàm s ố ồ ị ố
y = - 0,5x – 2 có đ th là (d’)ồ ị 0,5 đi mể
Đ th hàm s y = 2x + 3 là đng th ng c t tr c Ox t i ồ ị ố ườ ẳ ắ ụ ạ
(-1,5; 0) và c t tr c Oy t i (0; 3)ắ ụ ạ
Đ th hàm s y = - 0,5x – 2 là đng th ng c t tr c Ox ồ ị ố ườ ẳ ắ ụ
t i (- 4; 0) và c t tr c Oy t i (0; - 2)ạ ắ ụ ạ
10
5
5
10
15
8
6
4
2
2
4
6
x
O
B
N
M
y
d'
d
b) G i giao đi m c a d và d’ là H. Hãy tìm t a đ ọ ể ủ ọ ộ
c a đi m H?ủ ể
G i t a đ giao đi m c a hai đng th ng là H(xọ ọ ộ ể ủ ườ ẳ H; yH)
H(xH; yH) thu c đng th ng y = 2x + 3 nên yộ ườ ẳ H = 2xH + 3
H(xH; yH) thu c đng th ng y = - 0,5x – 2 nên yộ ườ ẳ H = -
0,5xH – 2
Suy ra: 2xH + 3 = - 0,5xH – 2
XH = - 2
Thay xH = - 2 vào yH = 2xH + 3 => yH = - 1
V y H(- 2; -1)ậ
0,5 đi mể
V
M
B
F
E
C
a) Ch ng minh t giác HMCN là hình ch nh tứ ứ ữ ậ
-Đi m C thu c đng tròn đng kính AB (gt)ể ộ ườ ườ
⇒ Góc ACB = 90° (tam giác có 1 c nh là đng kính c aạ ườ ủ
đng tròn ngo i ti p thì tam giác đó là tam giác vuông)ườ ạ ế
⇒ Góc MCN = 90° (1)
-M là hình chi u c a H trên AC (gt)ế ủ
⇒ Góc HMC = 90° (2)
-N là hình chi u c a H trên BC (gt)ế ủ
⇒ Góc HNC = 90° (3)
T (1), (2) và (3) ừ⇒ t giác HMCN là hình ch nh t (t ứ ữ ậ ứ
giác có ba góc vuông)
1,0 đi mể
b) Ch ng minh MN là ti p tuy n c a đng tròn ứ ế ế ủ ườ
đng kính BHườ
-G i F là trung đi m c a HBọ ể ủ
Tam giác HNB vuông t i Nạ
⇒ FH = FB = FN = BH/2
⇒ N thu c đng tròn tâm F đng kính BH (4)ộ ườ ườ
-G i MN giao v i CH t i Eọ ớ ạ
Có t giác HMCN là hình ch nh tứ ữ ậ
⇒ EH = EN = EC = EM (tính ch t hình ch nh t)ấ ữ ậ
Xét tam giác EHF và tam giác ENF có:
EH = EN (cmt)
EF c nh chungạ
FH = FN (cmt)
1,0 đi mể
⇒ Tam giác EHF b ng tam giác ENF (c.c.c)ằ
⇒ Góc EHF = góc ENF
Mà góc EHF = 90° (gt)
⇒ Góc ENF = 90°
⇒ MN ⊥ FN (5)
T (4) và (5) ừ⇒ MN là ti p tuy n c a đng tròn đngế ế ủ ườ ườ
kính BH
c) Ch ng minh MN vuông góc v i COứ ớ
Xét tam giác FNB cân t i Fạ
⇒ góc FNB = góc FBN
Xét tam giác COB cân t i Oạ
⇒ góc OCB = góc OBC
⇒ góc OCB = góc FBN
Mà góc OCB và góc FNB v trí đng vở ị ồ ị
⇒ CO song song FB
M t khác MN vuông góc v i FNặ ớ
(MN là tt t i N c a đng tròn đng kính BH)ạ ủ ườ ườ
Suy ra: MN vuông góc v i COớ
(quan h t vuông góc đn song song)ệ ừ ế
1,0 đi mể
d) Xác đnh v trí c a đi m C trên n a đng tròn ị ị ủ ể ử ườ
đng kính AB đ đo n th ng MN có đ dài ườ ể ạ ẳ ộ
l n nh t?ớ ấ
T giác HMCN là hình ch nh t ứ ữ ậ ⇒ MN = CH
MN l n nh t khi và ch khi CH l n nh tớ ấ ỉ ớ ấ
Tam giác CHO vuông t i Hạ
CH ≤ CO
CH l n nh t khi và ch khi CH = COớ ấ ỉ
H trùng O
Khi C là giao đi m c a đng th ng (qua O và vuông ể ủ ườ ẳ
góc v i AB) v i đng tròn tâm Oớ ớ ườ
0,5 đi mể