ĐỀ SỐ 9
Câu 1. Số phức
35i−+
có phần ảo bằng
A.
5i
. B.
5−
. C.
5
. D.
3−
.
Câu 2. Số phức
32i−
có phần thực bằng
A.
3−
. B.
. C.
3
. D.
2−
.
Câu 3. Số phức nào dưới đây là số thuần ảo?
A.
2z=
. B.
2zi=
. C.
13zi=+
. D.
32zi=+
.
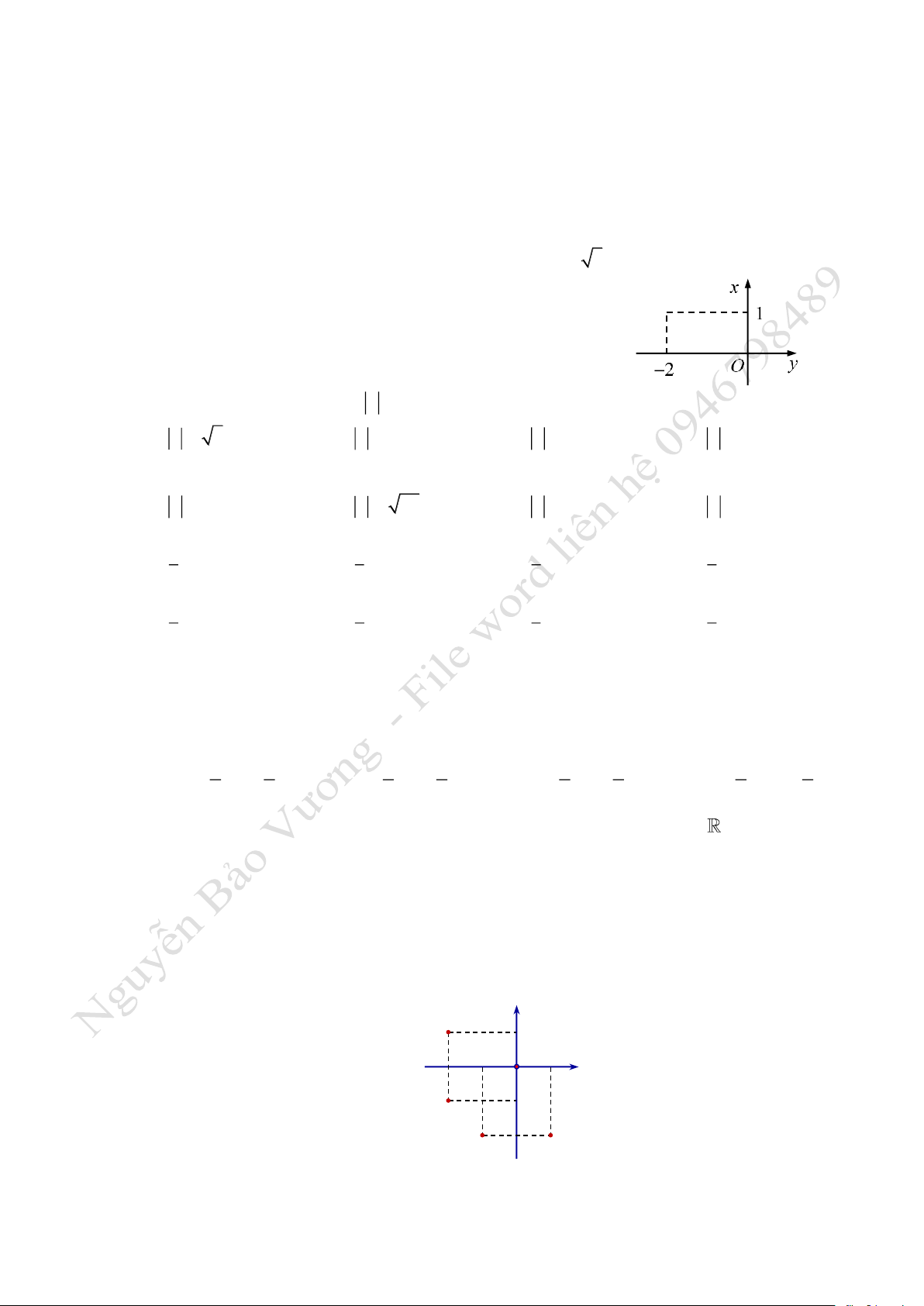
Câu 4. Số phức nào sau đây có điểm biểu diễn trên mặt phẳng tọa độ là
điểm
M
như hình bên?
M
A.
12zi=−
. B.
12zi=+
.
C.
2zi= − +
. D.
2zi=+
.
Câu 5. Cho số phức
12zi=+
. Tính
z
.
A.
5z=
. B.
3z=
. C.
5z=
. D.
1z=
.
Câu 6. Tính môđun của số phức
53zi= − +
.
A.
34.z=
B.
34.z=
C.
8.z=
D.
4.z=
Câu 7. Tìm số phức liên hợp của số phức
1 3 .zi=−
A.
3zi=−
. B.
3.zi=
C.
1 3 .zi=+
D.
1 3 .zi= − +
Câu 8. Cho số phức
2zi=
. Số phức liên hợp của
z
là:
A.
2zi=−
. B.
2zi=−
. C.
2zi=
. D.
2zi=+
.
Câu 9. Tìm các số thực
x
và
y
, biết
( ) ( )
3 2 2 1 2 3x y i x i+ + + = −
.
A.
2; 2xy= = −
. B.
2; 1xy= = −
. C.
2; 2xy= − = −
. D.
2; 1xy= − = −
Câu 10. Tìm các số thực
x
và
y
, biết
( ) ( ) ( ) ( )
3 2 2 1 1 5x y i x y i− + + = + − −
.
A.
34
;
23
xy= − =
. B.
24
;
33
xy==
. C.
34
;
23
xy==
. D.
34
;
23
xy= = −
.
Câu 11. Trong mặt phẳng phức, gọi
M
là điểm biểu diễn số phức
z a bi=+
(
,ab
),
M
là điểm
biểu diễn số phức liên hợp của
z
. Mệnh đề nào sau đây đúng?
A.
M
đối xứng với
M
qua
Oy
.
B.
M
đối xứng với
M
qua
Ox
.
C.
M
đối xứng với
M
qua đường thẳng
yx=
.
D.
M
đối xứng với
M
qua
O
.
Câu 12. Cho bốn điểm
A
,
B
,
C
,
D
trên hình vẽ biểu diễn 4 số phức khác nhau. Chọn mệnh đề sai.
A. Điểm
B
biểu diễn số phức
12zi=−
. B. Điểm
D
biểu diễn số phức
12zi= − +
.
C. Điểm
C
biểu diễn số phức
12zi= − −
. D. Điểm
A
biểu diễn số phức
2zi= − +
.
O
x
y
1
1−
1
1−
2−
2−
A
D
C
B
Câu 13. Trên mặt phẳng tọa độ
Oxy
tập hợp điểm biểu diễn số phức
z
thỏa mãn điều kiện: tổng bình
phương của phần thực và phần ảo của
z
bằng
1
, đồng thời phần thực của
z
không âm là
A. Nửa đường tròn tâm
O
bán kính bằng
1
, nằm phía trên trục
Ox
.
B. Nửa đường tròn tâm
O
bán kính bằng
1
, nằm phía dưới trục
Ox
.
C. Nửa đường tròn tâm
O
bán kính bằng
1
, nằm bên phải trục
Oy
.
D. Nửa đường tròn tâm
O
bán kính bằng
1
, nằm bên trái trục
Oy
.
Câu 14. Trên mặt phẳng tọa độ
Oxy
, cho các điểm
,,A B C
lần lượt là điểm biểu diễn của các số phức
1 ; 4 ;1 5i i i+ + +
. Tính bán kính đường tròn ngoại tiếp tam giác
ABC
.
A.
3.
2
B.
7.
2
C.
1.
2
D.
5.
2
Câu 15. Cho hai số phức
12
,zz
thỏa mãn
1217zz==
. Gọi
,MN
lần lượt là điểm biểu diễn của
12
,zz
trên mặt phẳng tọa độ. Biết
32MN =
, gọi
H
là đỉnh thứ tư của hình bình hành
MONH
và
K
là
trung điểm của
ON
. Tính
d KH=
.
A.
17
2
d=
. B.
52d=
. C.
3 13
2
d=
. D.
52
2
d=
Câu 16. Cho hai số phức
157zi=−
và
22 3 .zi=+
Tìm số phức
12
z z z=+
.
A.
74zi=−
. B.
25zi=+
. C.
25zi= − +
. D.
3 10zi=−
.
Câu 17. Tìm phần thực và phần ảo của số phức
32zi=+
.
A. Phần thực bằng
3−
và phần ảo bằng
2i−
.
B. Phần thực bằng
3−
và phần ảo bằng
2−
.
C. Phần thực bằng
3
và phần ảo bằng
2i
.
D. Phần thực bằng
3
và phần ảo bằng
2
.
Câu 18. Cho hai số phức
12zi=−
và
232zi=−
. Tìm phần ảo của số phức
12
.z z z=
.
A.
7−
. B.
11
. C.
3
. D.
2
.
Câu 19. Cho số phức
12zi=−
. Điểm nào dưới đây là điểm biểu diễn của số phức
w iz=
trên mặt
phẳng tọa độ?
A.
( )
1;2Q
. B.
( )
2;1N
. C.
( )
1; 2M−
. D.
( )
2;1P−
.
Câu 20. Cho hai số phức
11zi=+
và
22 3 .zi=−
Tính môđun của số phức
12
zz+
.
A.
12 13zz+=
. B.
12 5zz+=
. C.
12
1zz+=
. D.
12
5zz+=
.
Câu 21. Cho số phức
( )
3 4 3zi= − −
. Khi đó
z
có giá trị bằng
A.
15−
. B.
25
. C.
45
. D.
15
.
Câu 22. Tìm các số thực
,xy
thỏa mãn
2 (2 2 ) 7 4x y x y i i+ + − = −
.
A.
11 1
,
33
xy= − =
. B.
1, 3xy= − = −
. C.
1, 3xy==
. D.
11 1
,
33
xy= = −
.
Câu 23. Cho số phức
( )
, , 0z m ni m n m= +
thỏa mãn
1mn−=
và
5.z=
Tìm số phức
z
.
A.
32zi=+
. B.
2zi=+
. C.
12zi=−
. D.
2zi=−
.
Câu 24. Cho số phức
( ) ( )
2022 2022
1 2 2z i i= + +
. Tìm phát biểu đúng.
A.
z
là số thuần ảo. B.
là số thực.
C.
z
có phần ảo âm. D.
có phần thực dương.
Câu 25. Tập hợp các điểm biểu diễn số phức
z
thỏa mãn
13zi+ − =
là đường tròn có tâm và bán kính
lần lượt là
A.
( )
1; 1 ; 3IR−=
. B.
( )
1; 1 ; 9IR− − =
. C.
( )
1; 1 ; 3IR− − =
. D.
( )
1;1 ; 3IR−=
.
Câu 26. Tập hợp các điểm biểu diễn số phức
z
thỏa mãn
12z z i− = + −
trên mặt phẳng tọa độ là
A. đường thẳng. B. parabol. C. đường tròn. D. elip.
Câu 27. Mô đun của số phức
(1 )(2 )(3 2 )z i i i= + − +
bằng
A.
130
. B.
130
. C.
129
. D.
30 10
.
Câu 28. Số phức
z
thỏa mãn điều kiện
( )
3
2 1 6z i i+ − =
là
A.
32zi=+
. B.
2zi=+
. C.
22zi=−
. D.
2zi=−
.
Câu 29. Cho số phức
z
thỏa mãn điều kiện
13z iz i+ = +
. Tính tổng phần thực với phần ảo của số
phức đã cho.
A.
9
. B.
. C.
1
. D.
1−
.
Câu 30. Cho số phức
z
thỏa mãn
1z i z+ = −
và
2z−
nhỏ nhất. Tính
z
.
A.
2z=
. B.
1z=
. C.
2
2
z=
. D.
2z=
.
Câu 31. Nếu
23zi=+
thì
z
z
bằng
A.
5 12
13 13i−
B.
5 12
13 13i+
C.
34
77
i−
D.
56 2
11 ii
+−
Câu 32. Biểu diễn về dạng
z a bi=+
của số phức
( )
2020
2
12
i
zi
=+
là số phức nào?
A.
34
25 25i+
B.
34
25 25i−
C.
34
25 25i
−−
D.
34
25 25i
−+
Câu 33. Cho số phức
z a bi=+
( )
,ab
thỏa mãn
( )
2
1 . 4 5 1 6i z i i+ + − = − +
. Tính
S a b=+
A.
3S=
B.
8S=
C.
6S=
D.
3S=−
Câu 34. Cho số phức
5
1
1i
zi
+

=
−

. Tính
5 6 7 8
z z z z+ + +
.
A.
2−
B.
C.
4i
D.
4
Câu 35. Số phức nghịch đảo của số phức
13zi=+
là
A.
13i−
. B.
( )
113
10 i+
.
C.
( )
113
13 i
i+
+
. D.
( )
113
10 i−
.
Câu 36. Số phức nghịch đảo của số phức
( )
2
14zi= − +
là
A.
1 15 8
289 289
i
z
−
=+
. B.
1 15 8
289 289
i
z=+
.
C.
1 15 8
289 289
i
z=−
. D.
1 15 8
289 289
i
z
−
=−
.
Câu 37. Cho số phức
z
thỏa mãn:
( )( )
1 2 3 4 5 6 0z i i+ + + + =
. Tìm số phức
w1z=+
.
A.
71
25 25
zi
−
=+
. B.
71
25 25
zi=+
.
C.
71
25 25
zi
−
=−
. D.
71
25 5
zi
−
=+
.
Câu 38. Tìm phần ảo của số phức
z
thỏa mãn:
( ) ( )
2
1 2 1 3 5i z i i− + + =
.
A.
2
. B.
3
. C.
3−
. D.
2−
.
Câu 39. Tìm phần ảo của số phức
z
, biết
( )
2 1 3i z i− = +
.
A.
3
. B.
7
5i
. C.
7
5
. D.
1
5
−
.
Câu 40. Cho số phức
z
thỏa mãn
( )
1 3 5 7i z i+ − =
. Mệnh đề nào sau đây đúng?
A.
13 4
55
zi= − +
. B.
13 4
55
zi= − −
. C.
13 4
55
zi= − −
. D.
13 4
55
zi=+
.
Câu 41. Cho số phức
1
213
i
zi i
−+
= − + −
. Giá trị của
z
bằng
A.
2
. B.
23
. C.
2
. D.
10
.
Câu 42. Điểm
M
trong hình vẽ là điểm biểu diễn của số phức
z
. Giá trị của biểu thức
36
12
zi
i
−−
+
bằng
A.
3i+
. B.
3i−
. C.
3i−+
. D.
3i−−
.
Câu 43. Cho số phức
31
10 10
zi=+
. Trong mặt phẳng
Oxy
, điểm
M
là điểm biểu diễn của số phức
1
z
có tọa độ là
A.
( )
3;1M
. B.
( )
3;1M−
. C.
( )
3; 1M−−
. D.
( )
3; 1M−
.
Câu 44. Tìm số phức
z
biết
3
(1 3 )
1i
zi
−
=−
.
A.
44zi=+
. B.
44zi=−
. C.
44zi= − −
. D.
44zi= − +
.
Câu 45. Cho số phức
z
thỏa mãn
( ) ( )
1 2 3i z i z+ − − =
. Môđun của số phức
2
1
iz
wi
−
=−
là
A.
122
5
. B.
3 10
2
. C.
45
4
. D.
122
2
.
Câu 46. Giải phương trình
210zz− + =
trong tập số phức .
A.
31
22
zi=
. B.
3zi=
. C.
13zi=
. D.
13
22
zi=
.
Câu 47. Gọi
1
z
,
2
z
là hai nghiệm phức của phương trình
24 5 0zz− + =
trong tập số phức . Tìm phần
thực
a
của số phức
22
12
w z z=+
.
A.
0a=
. B.
8a=
. C.
16a=
. D.
6a=
.
Câu 48. Trong tập số phức , phương trình nào dưới đây nhận hai số phức
12i+
và
12i−
là
nghiệm? A.
22 3 0zz+ + =
. B.
22 3 0zz− − =
. C.
22 3 0zz− + =
. D.
22 3 0zz+ − =
.
Câu 49. Biết hai số phức có tổng bằng
3
và tích bằng
4
. Tổng môđun của hai số phức đó bằng
A.
7
. B.
. C.
10
. D.
12
.
Câu 50. Biết số phức
34= − +zi
là một nghiệm của phương trình
20+ + =z az b
, trong đó
,ab
là các
số thực. Tính
−ab
.
A.
31−
. B.
19−
. C.
1
. D.
11−
.
Câu 51. Kí hiệu
0
z
là nghiệm phức có phần ảo âm của phương trình
2
2 6 5 0zz− + =
. Hỏi điểm nào dưới
đây là điểm biểu diễn của số phức
0
iz
?
A.
113
;
22
M


. B.
231
;
22
M


. C.
331
;
22
M
−


. D.
413
;
22
M
−


.
Câu 52. Tổng môđun
4
nghiệm phức của phương trình
42
2 3 2 0zz− − =
là
A.
32
. B.
52
. C.
25
. D.
23
.
Câu 53. Gọi
1
z
và
2
z
là hai nghiệm của phương trình
22 10 0zz− + =
. Tính giá trị của biểu thức
22
12
P z z=+
.
A.
20P=
. B.
40P=
. C.
0P=
. D.
2 10P=
.
Câu 54. Gọi
12
,zz
là hai nghiệm phức của phương trình
22 3 0zz− + =
.Khi đó phần ảo của số phức
22
12
w z z=+
là
A.
2
. B.
. C.
22−
. D.
2−
.
Câu 55. Phương trình
20z az b+ + =
có một nghiệm phức là
12zi=+
.Giá trị biểu thức
ab+
là
A.
3
. B.
5
. C.
10−
. D.
3−
.
Câu 56. Gọi
12
,zz
là hai nghiệm phức của phương trình
22 4 0zz+ + =
. Giá trị của biểu thức
22
12
A z z=+
là
A.
8
. B.
8−
. C.
7−
. D.
4
.
Câu 57. Gọi
1
z
,
2
z
là các nghiệm của phương trình
28 25 0zz− + =
. Giá trị
12
zz−
bằng