ĐỀ KIỂM TRA CHÂT LƯƠNG CUỐI HỌC KỲ II
NĂM HOC 2020 – 2021
Môn: Toán – lơp 9. THCS
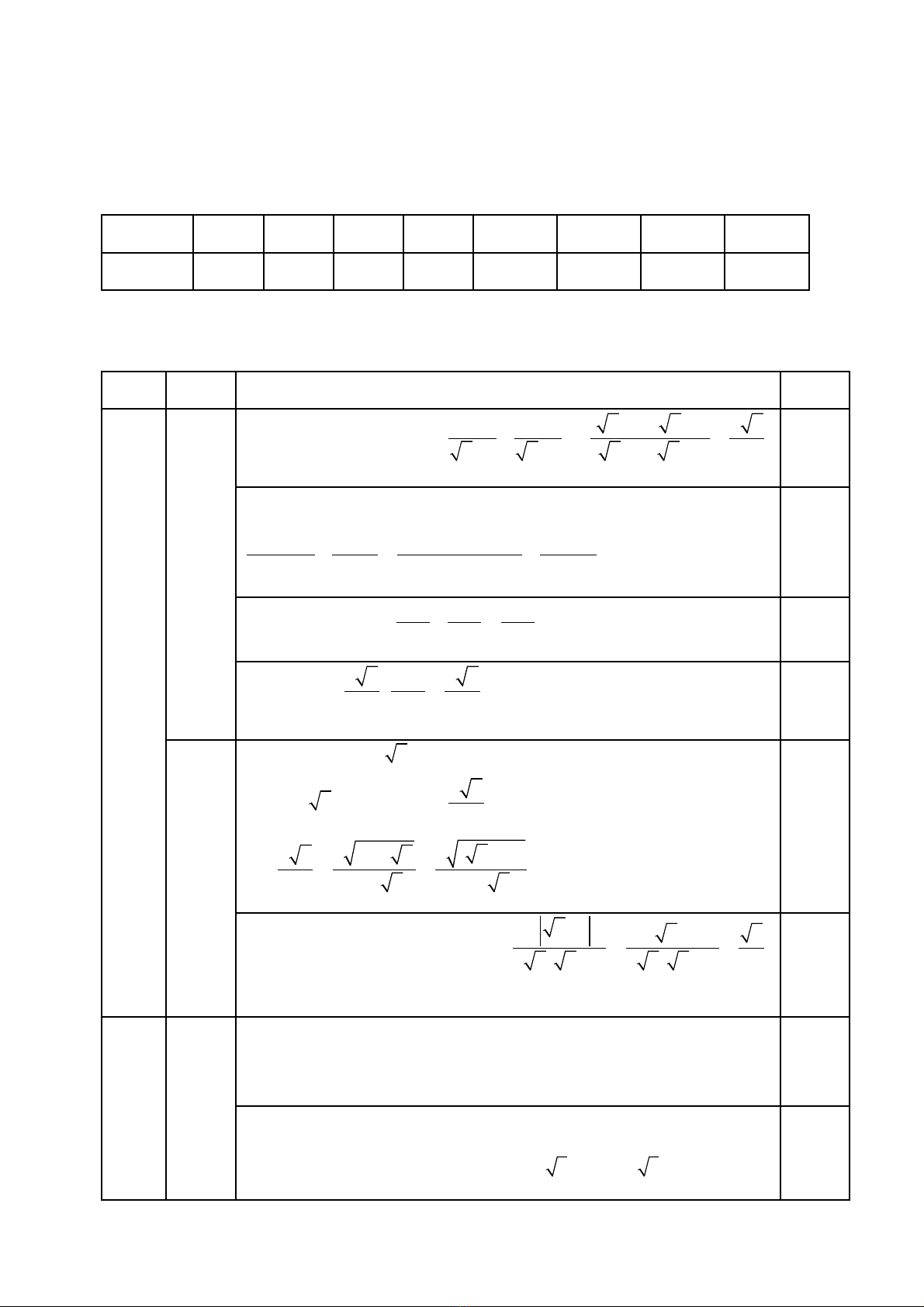
I. MA TRẬN ĐỀ.
Cấp độ
Tên
Chủ đề
Nhận biết Thông hiểu Vận dụng Cộng
Cấp độ thấp Cấp độ cao
TNKQ TL TNKQ TL TNKQ TL TNK
Q
TL
Chủ đề 1
Rút gọn biểu
thức
1 2
Số câu
Số điểm
Tỉ lệ %
Số
câu: 0
Số
câu
0
Số câu 1
Số điểm
0,25
Số
câu:
0
Số câu:
0
S.câu 2
S.điểm
1,5
Số
câu:
0
Số câu:
0
Số câu 3
Số điểm:
1,75= 17,5%
Chủ đề 2
Hệ pt
1
Số câu
Số điểm
Tỉ lệ %
Số
câu:0
Số
câu0
S.câu:0 Số
câu:
0
Số câu:
0
S.câu:1
S.điểm:
1,0
Số
câu:
0
S.câu:0 Số câu 1
Số điểm:1,0
= 10%
Chủ đề 3
Hàm số.
Phương trình
bậc hai 1 ẩn
4 2
Số câu
Số điểm
Tỉ lệ %
Số
câu: 0
Số
câu:
0
S.câu: 4
S.điểm:
1,0
Số
câu:
0
Số
câu:0
S.câu:2
S.điểm:
1,5
Số
câu
: 0
S.câu:0
S.điểm:
0
Số câu: 6
Số điểm:2,5
=25%
Chủ đề 4
Hình học
1 2 2 1
Số câu
Số điểm
Tỉ lệ %
S.câu:
1
S.điểm
0,25
Số
câu:
0
S. câu:
2
S.điểm:
0,5
Số
câu:
0
S.câu 0 S.câu:2
S.điểm:
2,0
Số
câu
: 0
S.câu:1
S.điểm:
1,0
Số câu: 6
Số điểm:3,75
=37,5%
Chủ đề 5
PT vô tỉ
1
Số câu
Số điểm
Tỉ lệ %
Số
câu: 0
Số
câu:
0
Số câu:
0
Số
câu:
0
S.câu 0 S.câu:0 Số
câu
: 0
S.câu:1
S.điểm:
1,0
Số câu: 1
Số điểm:1,0
=10%
Tổng số câu
Tổng số điểm
Tỉ lệ %
Số câu: 1
Số điểm: 0,25
= 2,5%
Số câu 7
Số điểm: 1,75
= 17,5%
Số câu 7
Số điểm: 6,0
= 60%
Số câu 2
Số điểm: 2,0
= 20%
Số câu 17
Số điểm10
=100%
II. ĐỀ:
SỞ GD-ĐT NAM ĐỊNH
TRƯỜNG THCS TT CỔ
LỄ ...................................
ĐỀ KIỂM TRA CHÂT LƯƠNG CUỐI HỌC KỲ II
NĂM HOC 2020 – 2021
Môn: Toán – lơp 9. THCS
(Thời gian làm bài: 90 phút.)
Đề khảo sát gồm 2 trang
Phần I. Trắc nghiêm (2,0 điêm). Hay chon phương an tra lơi đung va viêt chư cai đưng trươc
phương an đo vao bai lam.
Câu 1. ĐiêCu kiêDn đêE biêEu thưc
2 2 2015A x x= + + −
co nghiGa laC
A.
2x −
. B.
2x
> −
. C.
2x< −
. D.
2.x
−
Câu 2. Phương triCnh
2
3 2014 0x x m− − =
co hai nghiêDm trai dâu khi vaC chiE khi
A.
0.m>
B.
0m
<
. C.
0m
. D.
0.m
Câu 3. Gọi
1 2
,x x
là nghiệm của phương trình
.Giá trị của
2 2
1 2
x x
+
bằng
A.
1−
. B.
2
. C.
4
. D.
6
.
Câu 4. Trong mặt phẳng Oxy, parabol :
2
2y x
= −
có điểm chung với đường thẳng nào?
A.
6y=
. B.
2x
=
. C.
2 3y x= +
. D.
2 3y x= − +
.
Câu 5. Đường thẳng (d):
2 6y x= −
cắt trục tung tại điểm
A. M(0; -6). B.N(3; 0) C. P(0; 3). D. Q(-6;0)
Câu 6. Khi cắt hình trụ bởi một mặt phẳng vuông góc với trục hình trụ thì mặt cắt là hình gì?
A. Hình tròn. B. Hình tam giác. C. Hình chữ nhật. D. Hình thang.
Câu 7. Một hình nón có đường sinh l = 5dm và bán kính đường tròn đáy là r = 3dm. Chiều cao hình nón
bằng
A. 2dm. B. 4dm . C. 3dm . D. 5dm.
Câu 8. Một hình cầu có diện tích mặt cầu là
2
36 ( )S dm
π
=
thì thể tích của hình cầu đó bằng
A.
3
36( )dm
. B.
3
18 ( )dm
π
. C.
3
36 ( )dm
π
. D.
3
72 ( )dm
π
.
PhâXn II. Tư luân (8,0 điêm)
Câu 1. (1,5 điêm). Cho biểu thức
2 2
3 2
1 1 1
:1
1 1
x x x
Ax x x
x x
+ +
= + +
− −
− +
với
0x>
,
1x
.
ĐÊ CHINH THƯC
1) Rút gọn A.
2) Chứng minh với
3 2 2x= −
thì
2
2
A=
.
Câu 2.(1,5 điêm) Cho phương triCnh:
2 2
2 2 3 0x mx m m
− + − + =
(1), vơi m laC tham sô.
1) Giải phương trình (1) với m = 3.
2) Tìm tất cả các giá trị của m đêE (1) co hai nghiêDm
1 2
,x x
thoEa maGn
2 2
1 2 1 2
2( ) 5( )x x x x+ = +
.
Câu 3. (1,0 điểm) GiaEi hêD phương triCnh
1 2 5
2 1 3 4
x y
x y
− + =
− − = −
.
Câu 4. (3,0 điểm) Cho ba điểm A,B,C phân biệt thẳng hàng theo thứ tự đó. Vẽ đường tròn tâm O
bất kỳ đi qua hai điểm B, C (O không thuộc BC). Gọi E, F là các tiếp điểm của các tiếp tuyến kẻ từ
A tới đường tròn (O) . Gọi M là trung điểm BC.
1) Chứng minh các điểm A, E, O, M, F cùng nằm trên một đường tròn.
2) Gọi H là giao điểm của hai đường thẳng AO và EF. Chứng minh
. .AH AO AB AC=
.
3) Gọi K là giao điểm của FE và BC. Chứng minh
2
AK AK
AB AC
+ =
.
Câu 5. (1,0 điêm) GiaEi phương triCnh:
2 2
6 1 2 3 .x x x+ = − +
----------HẾT---------
III. HƯỚNG DẪN CHẤM
SỞ GD-ĐT NAM ĐỊNH ĐỀ KIỂM TRA CHẤT LƯƠNG CUỐI HỌC KỲ II
TRƯỜNG THCS TT CỔ LỄ NĂM HOC 2020 – 2021
HƯỚNG DẪN CHẤM MÔN TOÁN . LỚP 9.
Phần I. Trắc nghiệm (2,0 điểm) Mỗi câu đúng cho 0,25 điểm.
Câu 1 2 3 4 5 6 7 8
Đáp án D A D B A A B C
Phần II. Tự luận( 8,0 điểm)
Câu Ý Nội dung trình bày Điểm
1.
(1,5đ)
1)
(1,0 đ)
+ Với
0x>
,
1x
. ta có
1 1 1 1 2
1
1 1 ( 1)( 1)
x x x
x
x x x x
− + +
+ = =
−
+ − + −
0,25
+ Bến đổi
2 2 2 2
3 2 2
1 1
1 ( 1)( 1) ( 1)
x x x x x x
x x x x x x x x
+ + + +
+ = +
− − − + + −
0,25
1 1
1 1 1
x x
x x x
+
= + =
− − −
0,25
+Khi đó
2 1 2
:
1 1 1
x x x
Ax x x
+
= =
− − +
.
0,25
2)
(0,5 đ)
+ Ta thấy
3 2 2x= −
thỏa mãn điều kiện
0x
>
,
1
x
. Thay
3 2 2x= −
vào biểu thức
2
1
x
x+
ta được
2
2 ( 2 1)
2 2 3 2 2
14 2 2 4 2 2
x
Ax
−
−
= = =
+− −
.
0,25
2 2 1 2( 2 1) 2
2
2 2( 2 1) 2 2( 2 1)
−−
= = =
− −
(đpcm).
0,25
2.
(1,5đ)
1)
(0,5 đ)
Với m = 3 phương trình (1) trở thành:
2
6 6 0x x− + =
(*) 0,25
2
' ( 3) 6 3∆ = − − =
.
Phương trình (*) có các nghiệm
1 2
3 3; 3 3.x x= + = −
Kết luận: Khi m = 3 thì (1) có hai nghiệm
1 2
3 3; 3 3.x x= + = −
0,25
2)
(1,0 đ)
Ta có
2 2 2 2
' ( 2 3) 2 3m m m m m m∆ = − − + = − + −
2 3m
= −
.
Phương trình (1) có hai nghiệm
1 2
3
, ' 0 2 3 0 .
2
x x m m ∆ − ۳
0,25
Ta có
2 2 2
1 2 1 2 1 2 1 2 1 2
2( ) 5( ) 2( ) 4 5( ) 0.x x x x x x x x x x+ = + + − − + =
0,25
Theo hệ thức Vi – et ta có
2
1 2 1 2
2 ; 2 3.x x m x x m m+ = = − +
Do đó
2
1 2 1 2 1 2
2( ) 4 5( ) 0x x x x x x+ − − + =
0,25
2 2
2.(2 ) 4( 2 3) 5.(2 ) 0m m m m − − + − =
2
2
2 6 0 3
2
m
m m m
=
− − = −
=
Kết hợp với điều kiện
3
2
m
, ta được
2m=
là giá trị cần tìm.
0,25
3.
(1,0 đ)
ĐKXĐ:
1; 0.x y
0,25
Đặt
1u x
v y
= −
=
ĐK:
0; 0u v
. Hệ PT trở thành
2 5
2 3 4
u v
u v
+ =
− = −
.
0,25
Giải hệ phương trình ta được
1 1
1
22
x
u
vy
− =
=
==
0,25
2
4
x
y
=
=
.
Kết hợp với ĐKXĐ, hệ phương trình có nghiệm là
( ; ) (2; 4)x y =
.
0,25
Hình vẽ