TRƯỜNG PTDTNT THPT HĐB
TỔ TOÁN – LÝ – HÓA – TIN
KIỂM TRA ĐÁNH GIÁ GIỮA KÌ I TOÁN 12
Năm học 2022 – 2023
Tiết: 22-GT+11-HH – Ban: cơ bản
Thời gian: 90’ (Không kể thời gian giao đề)
Họ và tên học sinh: ........................................................ Lớp: 12….
Điểm Nhận xét, đánh giá của thầy cô giáo
I. Phần trắc nghiệm khách quan (7.0 điểm)
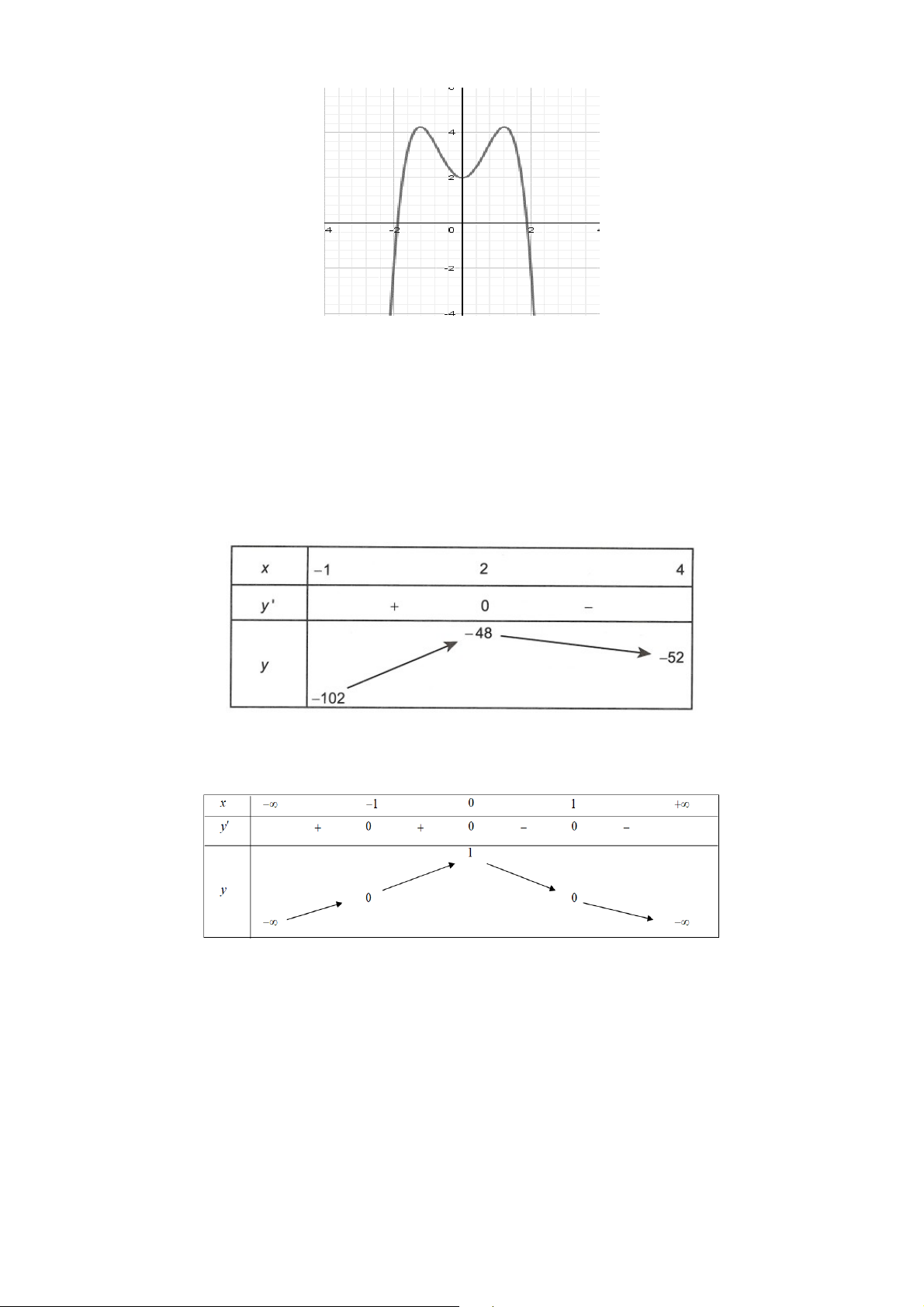
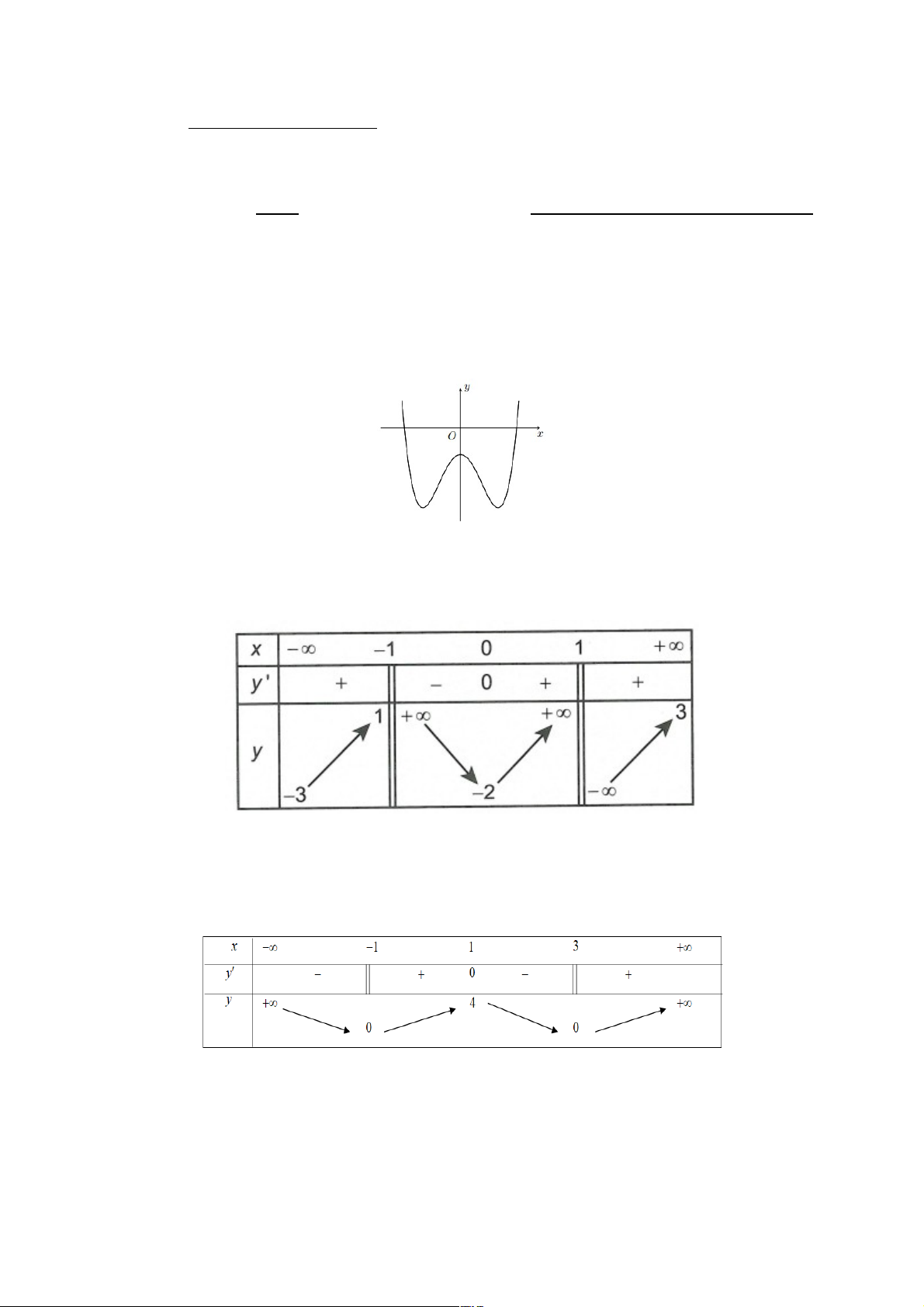
Câu 1: Cho hàm số có đồ thị như hình sau:
Mệnh đề nào sau đây đúng?
A. . B. .
C. . D. .
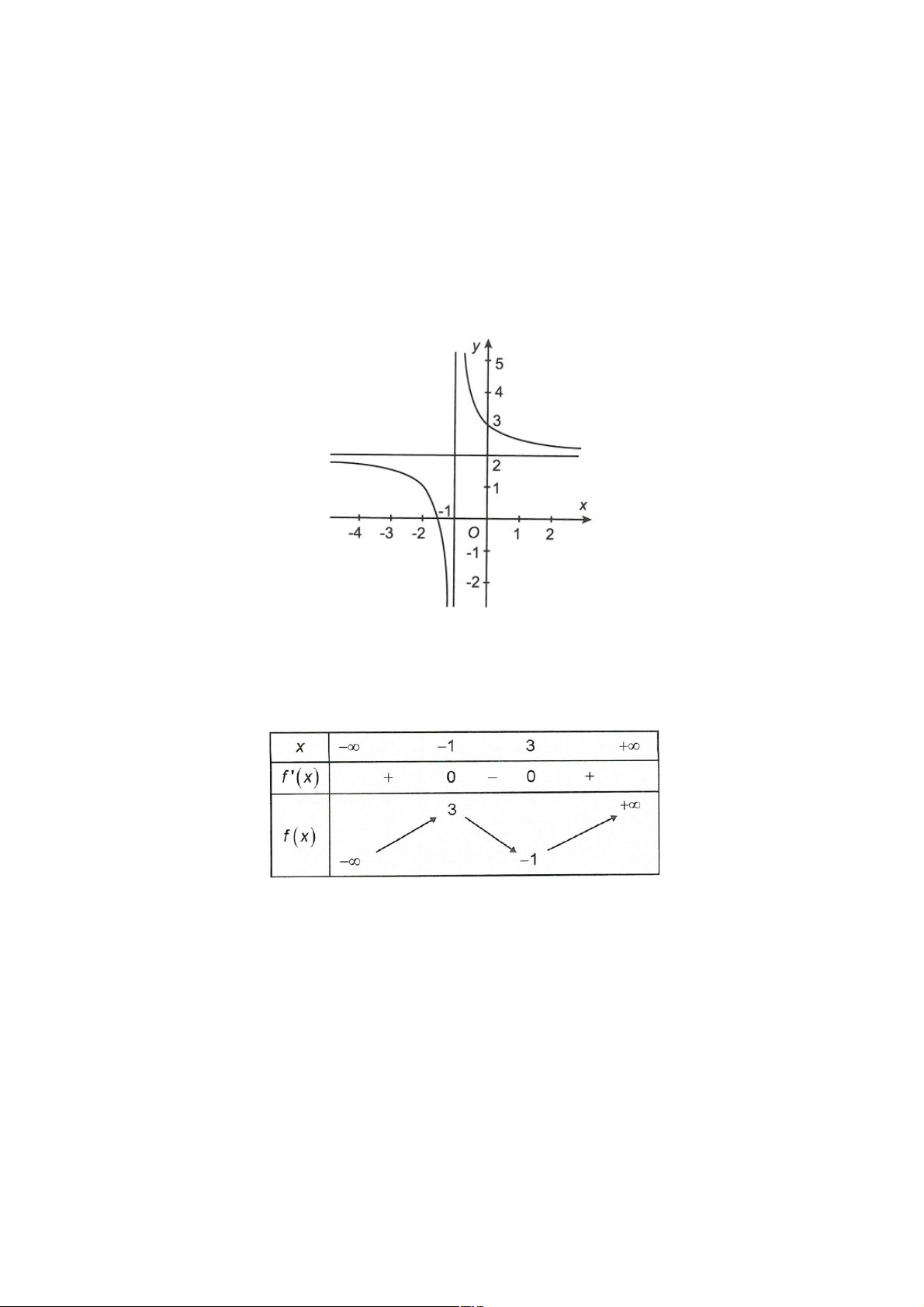
Câu 2: Cho hàm số có bảng biến thiên như sau:
Tổng số đường tiệm cận của đồ thị hàm số là
A. . B. . C. . D. .
Câu 3: Giá trị nhỏ nhất của hàm số trên đoạn bằng khi bằng
A. . B. . C. . D. .
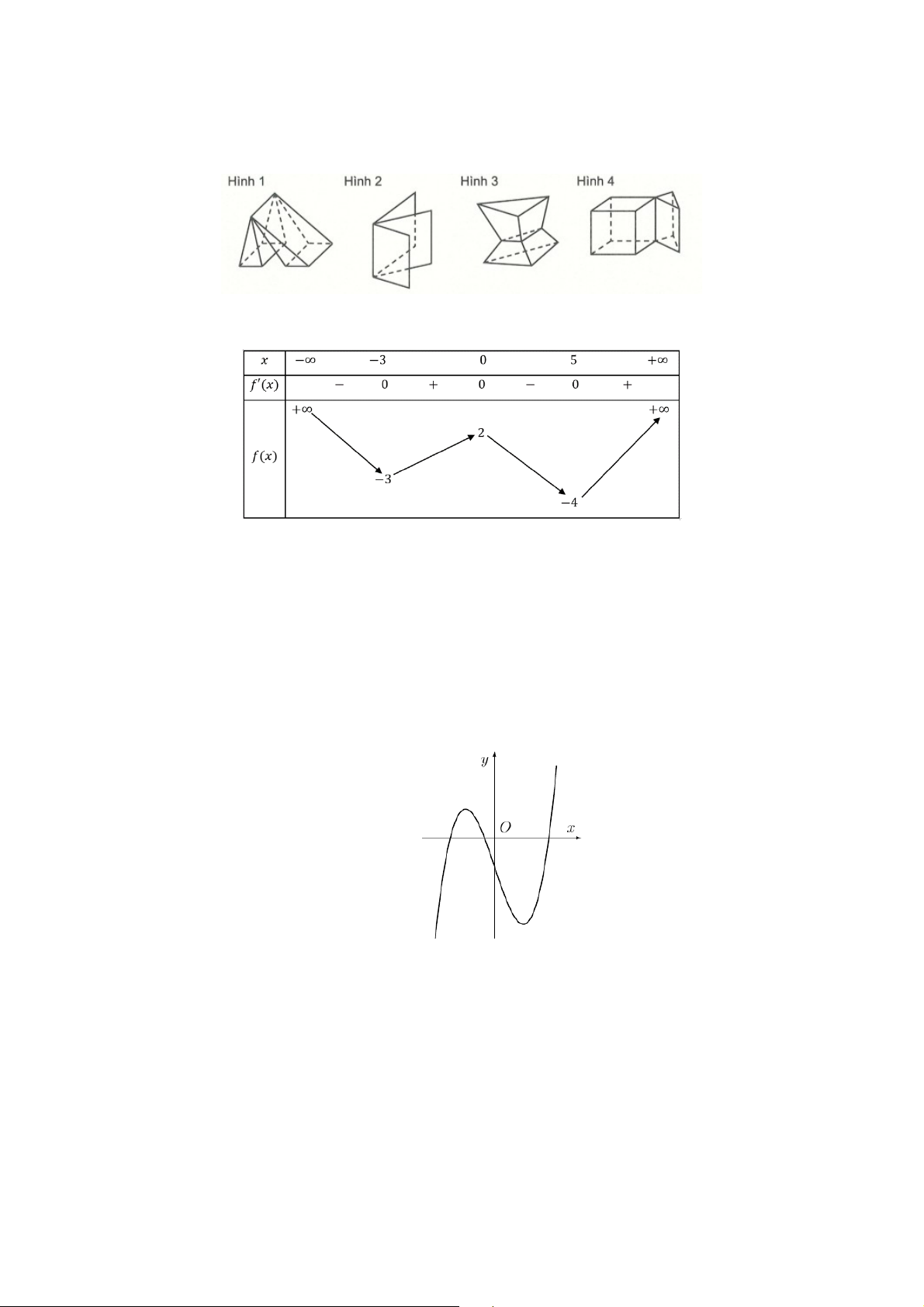
Câu 4: Cho hàm số có bảng biến thiên như sau:
Khẳng định nào sau đây là sai?
A. Hàm số đồng biến trên khoảng .
B. Hàm số nghịch biến trên khoảng .
C. Hàm số đồng biến trên khoảng .
D. Hàm số nghịch biến trên khoảng .
Trang 1/6 – Mã đề thi 907
Câu 5: Cho tứ diện có đôi một vuông góc và . Thể tích của tứ diện bằng
A. . B. . C. . D. .
Câu 6: Đồ thị hàm số có số đường tiệm cận là
A. . B. . C. . D. .
Câu 7: Cho khối hộp chữ nhật đứng có ba kích thước lần lượt bằng , , . Thể tích của khối hộp chữ
nhật đã cho bằng
A. . B. . C. . D. .
Câu 8: Cho hình lăng trụ đứng , đáy là tam giác ABC vuông tại A, cạnh hợp với mặt đáy góc .
Thể tích khối lăng trụ là
A. B. C. D.
Câu 9: Cho hàm số có đồ thị như hình sau:
Phương trình đường tiệm cận ngang của đồ thị hàm số là
A. . B. . C. . D. .
Câu 10: Cho hình chóp có đáy là tam giác đều cạnh . Biết và . Thể tích khối chóp bằng
A. . B. . C. . D. .
Câu 11: Cho hàm số có bảng biến thiên như sau:
Điểm cực tiểu của hàm số đã cho là
A. . B. . C. . D. .
Câu 12: Giá trị nhỏ nhất của hàm số trên (2; 6) là
A. . B. . C. . D. .
Trang 2/6 – Mã đề thi 907
Câu 13: Hàm số nào dưới đây có ba cực trị?
A. . B. .
C. . D. với là tham số thực.
Câu 14: Trong các hình dưới đây, hình nào là hình đa diện?
A. Hình 4. B. Hình 1. C. Hình 2. D. Hình 3.
Câu 15: Cho hàm số có bảng biến thiên như hình vẽ sau:
Tất cả các giá trị của tham số để phương trình có đúng hai nghiệm phân biệt là
A. hoặc . B. .
C. . D. .
Câu 16: Cho hình chóp có đáy ABC là tam giác vuông tại B, , cạnh bên SA vuông góc với mặt
phẳng đáy và SB tạo với mặt đáy một góc bằng . Thể tích của khối chóp là
A. . B. . C. . D. .
Câu 17: Cho hình chóp S.ABC, trên các cạnh AB, BC, SC lần lượt lấy các điểm M, N, P sao cho .
Tỉ số thể tích của hai khối chóp S.BMN và A.CPN bằng
A. . B. . C. . D. .
Câu 18: Hàm số nào dưới đây có đồ thị như đường cong trong hình bên?
A. . B. . C. . D. .
Câu 19: Cho hàm số có và . Mệnh đề nào dưới đây đúng?
A. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
B. Đồ thị hàm số đã cho có hai tiệm cận ngang là và
C. Đồ thị hàm số đã cho có hai tiệm cận ngang là và .
D. Đồ thị hàm số đã cho có hai tiệm cận đứng là và .
Câu 20: Cho khối chóp có diện tích đáy
3B
=
và chiều cao
2h
=
. Thể tích khối chóp đã cho bằng
A.
3
.B.
6
.C.
12
.D.
2
.
Câu 21: Cho hàm số có đồ thị như hình vẽ sau:
Trang 3/6 – Mã đề thi 907
Số điểm cực trị của đồ thị hàm số là
A. . B. . C. . D. .
Câu 22: Giá trị của tham số m để hàm số đạt cực đại tại điểm x = 3 là
A. B. C. D.
Câu 23: Tất cả các giá trị của tham số để đồ thị hàm số có đường tiệm cận đứng là
A. . B. . C. . D. .
Câu 24: Tất cả các giá trị của tham số để hàm số đồng biến trên từng khoảng xác định của nó
là
A. . B. . C. . D. .
Câu 25: Cho hàm số có bảng biến thiên trên đoạn như sau:
Giá trị lớn nhất của hàm số trên đoạn bằng
A. . B. . C. . D. .
Câu 26: Cho hàm số liên tục trên và có bảng biến thiên của hàm số như sau:
Hàm số đồng biến trên khoảng
A. . B. . C. . D. .
Trang 4/6 – Mã đề thi 907
Câu 27: Cho hàm số có đồ thị như hình sau:
Hàm số nghịch biến trên khoảng
A. . B. . C. . D. .
Câu 28: Cho hàm số xác định trên tập và có đạo hàm . Khẳng định nào sau đây đúng?
A. Hàm số đã cho nghịch biến trên khoảng .
B. Hàm số đã cho đồng biến trên khoảng .
C. Hàm số đã cho nghịch biến trên khoảng .
D. Hàm số đã cho đồng biến trên khoảng .
Câu 29: Cho khối lăng trụ có thể tích là , đường cao có độ dài bằng . Diện tích đáy của khối lăng
trụ đã cho bằng
A. . B. . C. . D. .
Câu 30: Cho hàm số có đồ thị như hình vẽ sau:
Giá trị cực tiểu của hàm số bằng
A. . B. . C. . D. .
Câu 31: Cho hình chóp tam giác đều có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng . Thể
tích khối chóp là
A. . B. . C. . D. .
Câu 32: Hàm số nghịch biến trên khoảng
A. . B. . C. . D. .
Câu 33: Số điểm cực đại của hàm số là
A. . B. . C. . D. .
Câu 34: Cho hình lăng trụ đứng có đáy là tam giác đều cạnh bằng và hợp với mặt đáy một góc .
Thể tích khối lăng trụ bằng
A. . B. . C. . D. .
Câu 35: Giá trị nhỏ nhất của hàm số trên đoạn là
A. . B. . C. . D. .
II. Phần tự luận (3.0 điểm)
Bài 1. Tìm giá trị tham số để hàm số nghịch biến trên khoảng .
Bài 2. Tìm giá trị lớn nhất của hàm số trên đoạn .
Bài 3. Tìm tập hợp tất cả các giá trị tham số để hàm số đạt cực đại tại .
Bài 4. Cho hình chóp có đáy là hình vuông cạnh Tam giác đều và nằm trong mặt phẳng vuông
góc với mặt đáy. Tính thể tích của khối chóp .
BÀI LÀM
I. TRẮC NGHIỆM
Câ
u
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Đ/
Trang 5/6 – Mã đề thi 907