UBND QUẬN BÌNH THẠNH
TRƯỜNG TRUNG HỌC CƠ SỞ
CỬU LONG
ĐỀ ĐỀ NGHỊ
(Đề gồm 2 trang)
ĐỀ KIỂM TRA GIỮA HỌC KÌ II
NĂM HỌC: 2024 – 2025
MÔN: TOÁN 9
Thời gian: 90 phút
(không tính thời gian phát đề)
PHẦN 1. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm).
Câu 1: Hàm số
2
y 3x= −
đồng biến khi
A.
x0≥
. B.
x0<
. C.
x0≤
. D.
x0>
.
Câu 2: Khẳng định nào sau đây là đúng. Đồ thị của hàm số
( )
2
y ax a 0= ≠
A. Với
a0>
, đồ thị nằm trên trục hoành và O là điểm cao nhất đồ thị.
B. Với
a0<
, đồ thị nằm dưới trục hoành và O là điểm cao nhất đồ thị.
C. Với
a0>
, đồ thị nằm dưới trục hoành và O là điểm thấp nhất đồ thị.
D. Với
a0<
, đồ thị nằm dưới trục hoành và O là điểm thấp nhất đồ thị.
Câu 3: Phương trình nào là phương trình bậc hai một ẩn?
A. 0x2 + 5x + 2 = 0 B. 6x2 + y + 5 = 0 C. x2 - 1 = 0 D. 2x + y = 3
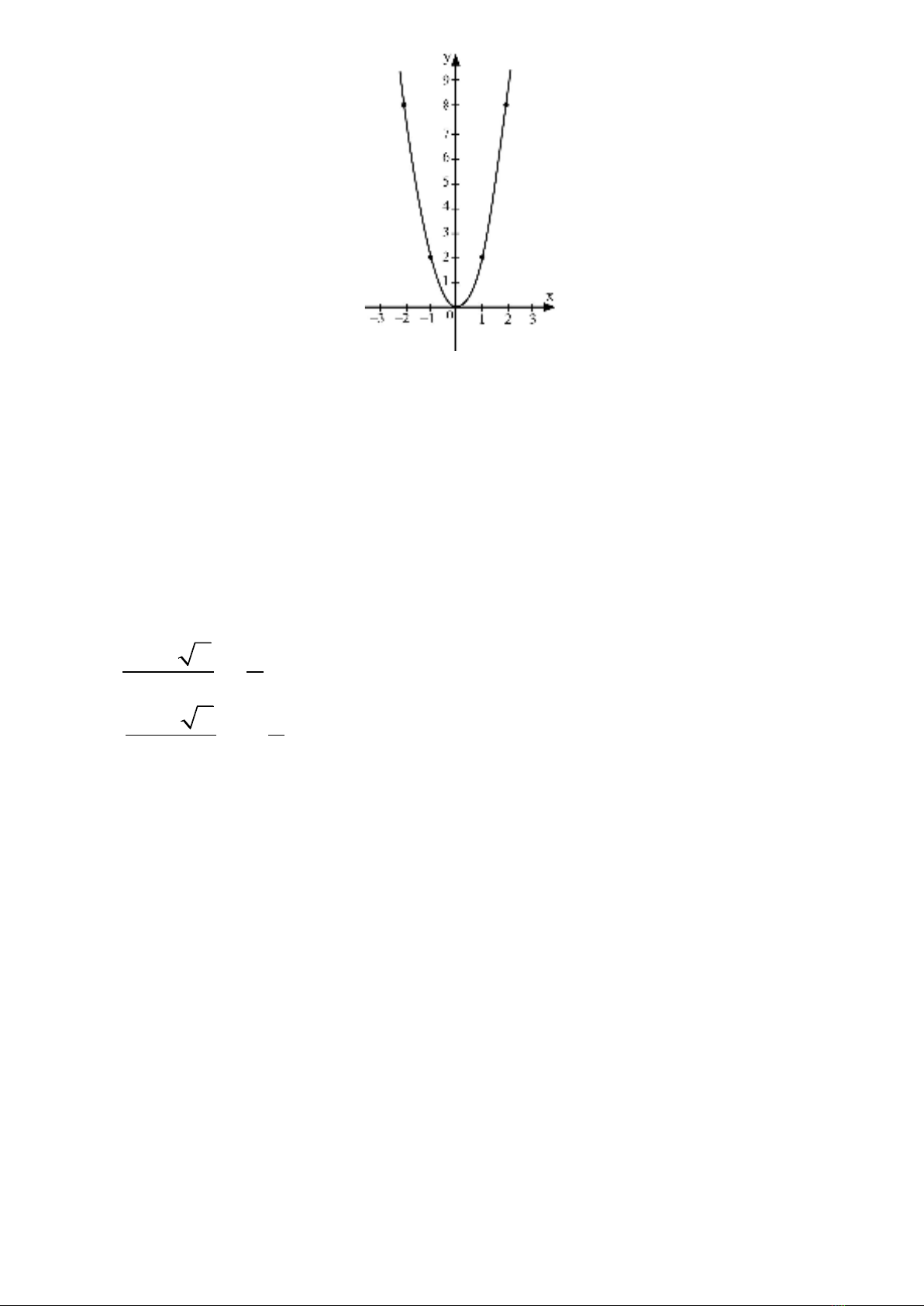
Câu 4: Điểm thuộc (P): y =
1
2
x2 là
A. (2; 1) B. (2; 8 ) C. (2; 4) D. (2; 2)
Câu 5: Phương trình:
có hai nghiệm phân biệt khi nào?
A.
0∆>
B.
0∆<
C.
0∆≤
D.
0∆=
Câu 6: Cho phương trình
214 33 0xx 
. Không giải phương trình, hãy tính tổng và tích các nghiệm,
hãy chọn câu đúng:
A.
1 2 12
33; 14x x xx
B.
1 2 12
14; 33x x xx
;
C.
1 2 12
11; 3x x xx
D.
1 2 12
14; 33x x xx 
;
Câu 7: Tứ giác ABCD nội tiếp đường tròn có
A
= 500. Khi đó
C
bằng:
A. 400 B . 500 C . 1000 D . 1300
Câu 8: Đường tròn ngoại tiếp đa giác là đường tròn
A. chứa đa giác đó.
B. nằm ngoài đa giác đó.
C. tiếp xúc với tất cả các cạnh của đa giác đó.
D. đi qua tất cả các đỉnh của đa giác đó.
Câu 9: Tâm đường tròn nội tiếp của một tam giác là giao của các đường:
A. Trung trực B. Phân giác trong
C. Phân giác ngoài D. Đáp án khác
Câu 10: Một tứ giác nội tiếp đường tròn là
A. Tứ giác nằm bên trong đường tròn.
B. Tứ giác có 4 đỉnh nằm ngoài một đường tròn.
C. Tứ giác có 4 đỉnh nằm trên một đường tròn.
D. Tứ giác có 4 đỉnh nằm trong một đường tròn.
Câu 11. Tam giác đều là một đa giác
A. Có 3 cạnh và 3 góc bằng nhau. B. Có 7 cạnh và 7 góc bằng nhau.
C. Có các cạnh và các góc bằng nhau. D. Có 8 cạnh và 8 góc bằng nhau
Câu 12. Các phép quay có thể có với một đa giác đều tâm O là
A. Phép quay thuận chiều và phép quay đảo chiều.
B. Phép quay thuận chiều và phép quay ngược chiều.
C. Phép quay xuôi chiều và phép quay đảo chiều.
D. Phép quay xuôi chiều và phép quay ngược chiều.
PHẦN 2: TỰ LUẬN (7 điểm)
Bài 1. (1,5 điểm) Cho parabol (P):
2
2yx=
.
a. Vẽ đồ thị (P) trên hệ trục tọa độ.
b. Tìm tọa độ những điểm M thuộc (P) có tung độ bằng 2.
Bài 2 (0,5 điểm) Giải phương trình sau : 6x2 – 7x – 3 = 0.
Bài 3. (1 điểm) Giải bài toán bằng cách lập phương trình bậc hai
Một sân bóng hình chữ nhật có chiều dài là x (đơn vị: mét, x > 0) và chiều dài hơn chiều rộng là 3 m.
a) Viết biểu thức tính diện tích S của sân bóng theo x.
b) Nếu tăng chiều dài thêm 1 m và tăng chiều rộng thêm 3 m thì diện tích sân bóng tăng gấp đôi.
Tính chiều dài của sân bóng đó.
Bài 4. (1,5 điểm) Cho phương trình:
2x2 + 3x – 14 = 0 có 2 nghiệm là
12
,xx
a. Chứng minh phương trình có hai nghiêm.
b. Tính giá trị của biểu thức sau:
2
1 2 12
()P x x xx=−+
Bài 5. (2,5 điểm) Cho tam giác ABC nhọn (với AB < AC) nội tiếp (O;R). Các đường cao AD,BE,CF
của tam giác ABC cắt nhau tại H. Gọi I là trung điểm của BC.
a)Chứng minh:tứ giác BFEC nội tiếp đường tròn đường kính BC và OI vuông góc BC.
b)Kẻ đường kính AM của (O). Chứng minh: AC.AB =AD.AM và ba điểm H,I,M thẳng hàng.
c)Biết AH = R = 10cm. Tính độ dài đoạn thẳng BC và EF.
Đáp án:
PHẦN I. TRẮC NGHIỆM (3,0 điểm). Mỗi câu đúng được 0,25 điểm.
1
2
3
4
5
6
7
8
9
10
11
12
B B C D B B D D B C A B
PHẦN II. TỰ LUẬN (7,0 điểm).
Bài 1. (1,5 điểm)
Lập bảng giá trị của (P) .................................................................................................................. 0,25đ
Bảng giá trị:
x
–2
–1
0
1
2
y = 2x2
8
2
0
2
8
Vẽ (P) ............................................................................................................................................. 0,25đ
Đồ thị của hàm số được vẽ như hình sau
b) Điểm M thuộc (P) có tung độ bằng 2 nên tọa độ của M thỏa mãn:
2
22x
khi
2
1x
....................................................................................................................... 0,25đ
Khi đó
1x
hoặc
1x
Với
1x
thì
2y
........................................................................................................................ 0,25đ
Với
1x
thì
2y
.................................................................................................................... 0,25đ
Vậy tọa độ những điểm M thuộc (P) có tung độ bằng 2 là
(1; 2 )
và
1; 2
.................................. 0,25đ
Bài 2.
6x2 - 7x - 3 = 0
∆
= 121 > 0
Phương trình có 2 nghiệm phân biệt:
1
2
3
*22
1
*23
b
xa
b
xa
−+
= =
−−
= = −
Bài 3.
a) Viết biểu thức tính diện tích 𝑺𝑺 của sân bóng theo 𝒙𝒙.
Chiều rộng của sân bóng là: 𝑥𝑥 − 3 (𝑚𝑚)
Diện tích của sân bóng là: 𝑆𝑆=𝑥𝑥(𝑥𝑥 − 3)=𝑥𝑥2−3𝑥𝑥 (𝑚𝑚2)
b) Sau đó người ta tăng chiều dài thêm 𝟏𝟏 m và tăng chiều rộng thêm 𝟑𝟑 𝐦𝐦 thì diện tích sân bóng
tăng gấp đôi. Tính chiều dài của sân bóng đó?
Diện tích của hình chữ nhật sau khi tăng chiều dài thêm 1 m và tăng chiều rộng thêm 3 m là:
(𝑥𝑥+ 1)(𝑥𝑥 − 3 + 3) = (𝑥𝑥+ 1) ⋅ 𝑥𝑥 =𝑥𝑥2+𝑥𝑥.
Theo bài ta có phương trình: 𝑥𝑥2+𝑥𝑥= 2(𝑥𝑥2−3𝑥𝑥)
𝑥𝑥2−7𝑥𝑥= 0
𝑥𝑥(𝑥𝑥 − 7)= 0
�𝑥𝑥= 0
𝑥𝑥= 7 ⇒ 𝑥𝑥 = 7 (vì 𝑥𝑥> 0)
Vậy chiều dài của hình chữ nhật là 7 𝑚𝑚 .
Bài 4.
a) Chứng tỏ phương trình có 2 nghiệm phân biệt ( 0,5đ)
Theo viết
12
12
3
2
7
b
Sxx a
c
P xx a
−−
=+= =
= = = −
( 0,5đ)
b, Ta có:
( )
2
1 2 12
P x x xx=−+
22
1 2 12
P x x xx=+−
( 0,5đ)
( )
2
1 2 12
3P x x xx=+−
( 0,25đ)
( )
2
337
2
P−

= −−


93
4
P=
( 0,25đ)
Bài 5.
a)Chứng minh tứ giác BFEC nội tiếp đường tròn tâm I đường kính BC .
*C/m ba điểm B ,F ,C cùng thuộc đường tròn tâm I đường kính BC .
*C/m ba điểm B , E ,C cùng thuộc đường tròn tâm I đường kính BC .
Ta có bốn điểm B,F,E,C cùng thuộc đường tròn tâm I đường kính BC
Vậy tứ giác BFEC nội tiếp đường tròn tâm I đường kính BC .
Chứng minh OI
⊥
BC .
C/m tam giác OBC cân tại O và có OI là trung tuyến
Nên OI cũng là đường cao tam giác OBC
Suy ra OI
⊥
BC.
b) Chứng minh AB.AC = AD.AM
C/m 2 tam giác ADB và ACM đồng dạng ( g-g)
Suy ra AD/ AC = AB / AM
Suy ra AB.AC = AD.AM.
Chứng minh ba điểm H,I,M thẳng hàng
*C/m : MC // BH
*C/m : MB // CH
Suy ra Tứ giác BHCM là hình bình hành
M
I
D
F
H
E
O
B
C
A
Lại có I là trung điểm của BC
Nên I cũng là trung điểm của HM
Suy ra ba điểm H , I , M thẳng hàng .
c)Tính độ dài đoạn thẳng BC
Tính OI
*OI = ½ AH = ½ .10 = 5 (cm )
*Xét tam giác OIC vuông tại I
Ta có OI2 +IC2 = OC2 (đl pytago)
IC =
22
10 5 5 3−=
(cm).
*BC = 2 IC = 10
3
(cm).
Tính độ dài đoạn thẳng EF
*cos IOC = OI / OC = 5/10 = ½
Góc IOC = 600
Suy ra góc BOC = 2 góc IOC = 1200
*Ta có góc BAC = ½ góc BOC = 600 ( góc nội tiếp và góc ở tâm cùng chắn cung BC)
* Chứng minh Tam giác AEF và ABC đồng dạng
Suy ra EF /BC = AE/AF = cos BAC = cos 600 =1/2
Suy ra EF = ½ BC
Suy ra EF = 5
3
(cm)