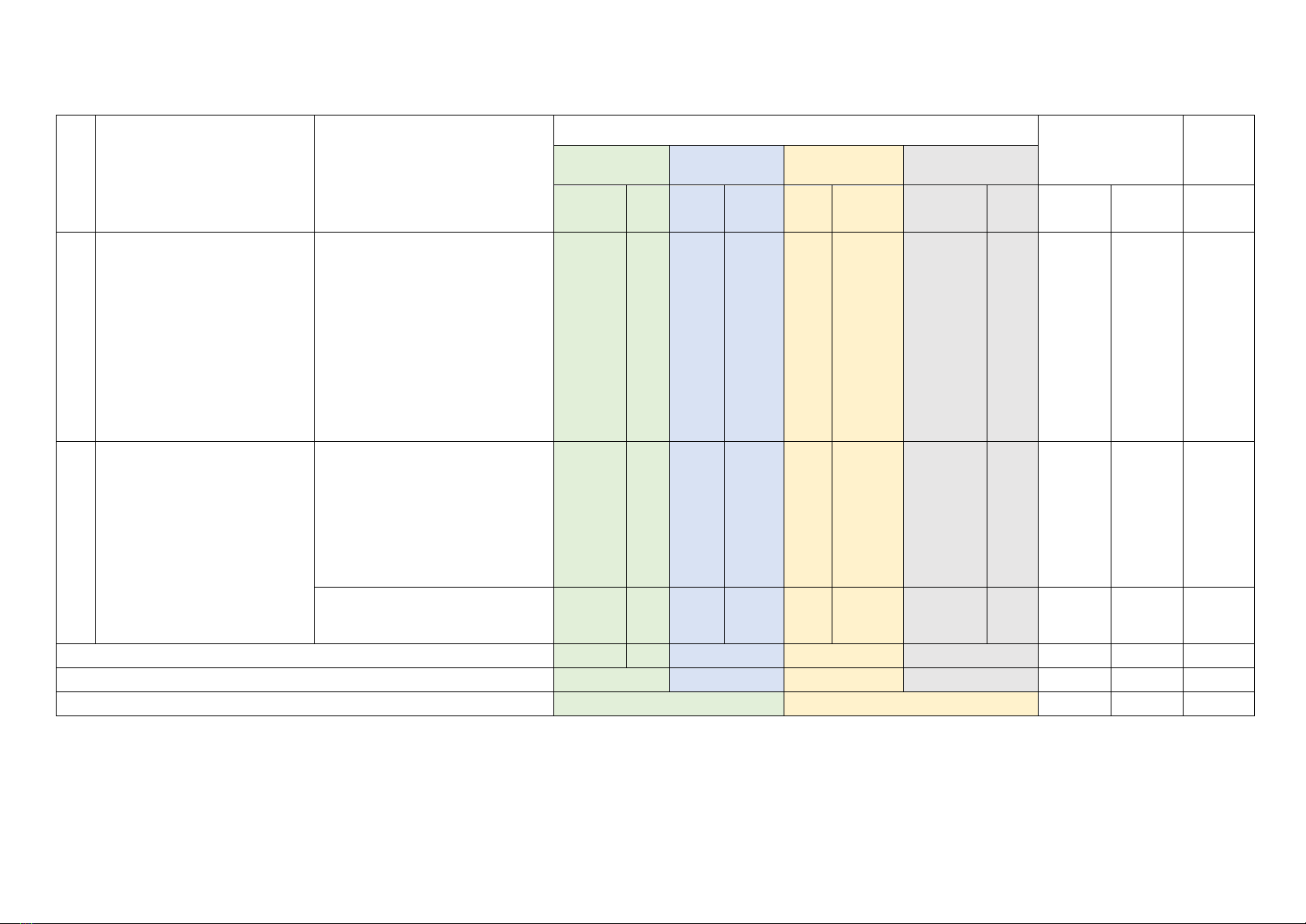
MA TRẬN ĐỀ KIỂM TRA GIỮA KỲ II – TOÁN 9
A. BẢNG MA TRẬN ĐỀ KIỂM TRA.
T
T Chủ đề Nội dung/Đơn vị kiến thức
Mức độ đánh giá
Tổng số câu
Tổng
%
điểm
Nhận biết Thông hiểu Vận dụng Vận dụng cao
TNK
Q
T
L
TN
KQ
TL
TN
KQ
TL TNKQ TL
TNK
Q
TL
1
HÀM SỐ Y = ax2 ( a
≠0) VÀ PHƯƠNG
TRÌNH BẬC HAI
MỘT ẨN
Hàm số và đồ thị hàm số y
= ax2 ( a ≠ 0)
Phương trình bậc hai một ẩn
Định lí vi-et
6
4
(Bài
1a,b
;2;
4a)
2
(Bài 3,
4b)
6 6 60,0
2 TỨ GIÁC NỘI TIẾP.
ĐA GIÁC ĐỀU
Đường tròn ngoại tiếp tam
giác. Đường tròn nội tiếp
tam giác
Tứ giác nội tiếp
4
1
(Bài
5a)
1
( Bài
5b)
1
(Bài
5c)
4 3 35,0
Đa giác đều và phép quay
2 2 5,0
12
5
3
2
12
9
30%
35%
25%
10%
100
65%
35%
100
UBND QUẬN BÌNH THẠNH
TRƯỜNG THCS ĐỐNG ĐA
ĐỀ THAM KHẢO
ĐỀ KIỂM TRA GIỮA KỲ II NĂM HỌC 2024 - 2025
MÔN TOÁN LỚP 9
Thời gian: 90 phút (không kể thời gian phát đề)
A. TRẮC NGHIỆM: (3,0 điểm)
Câu 1: Trong những điểm sau đây, điểm nào thuộc đồ thị hàm số y = 2x2 ?
A.
( )
2;3
.
B. (2; 8).
C.
( )
2;5−
.
D. (-2; - 8)
Câu 2: Đồ thị hàm số
( )
2
,0y ax a= ≠
đi qua điểm A(2; -4). Giá trị của a bằng:
A. 1.
B. -1.
C. 2.
D. - 4.
Câu 3: Phương trình nào dưới đây không là phương trình bậc hai một ẩn?
A. x2 – 4x = 0
B. 3x2 + 5x – 2 = 0.
C. 2x2 – 2 365 = 0.
D. 0x2 –7x + 25 = 0.
Câu 4: Nghiệm của phương trình x2 – 14x + 13 = 0 là:
A. x
1
= – 1; x
2
= 13.
B. x
1
= – 1; x
2
= – 13.
C. x
1
= 1; x
2
= – 13.
D. x
1
= 1; x
2
= 13.
Câu 5: Gọi S và P lần lượt là tổng và tích của hai nghiệm của phương trình x2 + 5x – 10 = 0.
Khi đó giá trị của S và P là:
A. S = 5; P = 10
B. S = - 5; P = 10
C. S = - 5; P = - 10
D. S = 5; P = - 10
Câu 6: Cho phương trình x2 + 7x – 15 = 0. Gọi x
1
, x
2
là hai nghiệm của phương trình. Khi đó
giá trị của biểu thức x12 + x22 - x1x2 là :
A. 79
B. 94
C. -94
D.-79
Câu 7: Trong các phát biểu sau phát biểu nào sai ?
A. Hình vuông nội tiếp đường tròn.
B. Mọi tứ giác đều nội tiếp đường tròn.
C. Hình chữ nhật là tứ giác nội tiếp.
D. Tổng số đo hai góc đối trong tứ giác nội tiếp bằng 1800.
Câu 8: Cho ∆ABC đều cạnh a nội tiếp trong đường tròn tâm O có bán kính R thì:
A.
3
3
a
R=
B.
3
2
a
R=
C.
3
6
a
R=
D.
2
3
4
a
R=
Câu 9: Cho tam giác đều cạnh 3cm. Bán kính của đường tròn nội tiếp tam giác đều đó là:
A.
33 .
2cm
B.
2.
2cm
C.
3.
2cm
D.
23 .
3cm
Câu 10: Cho tứ giác MNPQ nội tiếp đường tròn (O; R) và
0
ˆ60M=
. Số đo của
ˆ
P
là:
A. 1200
B. 300
C. 1800
D. 900
Câu 11: Cho lục giác đều ABCDEF nội tiếp đường tròn bán kính R. Độ dài cạnh AB bằng:
A.
R
B.
3R
C.
3
2
R
D.
2
R
Câu 12: Cho tam giác đều ABC có O là tâm đường tròn ngoại tiếp. Phép quay nào với O là tâm
biến tam giác ABC thành chính nó?
A. 900
B. 1000
C. 1100
D. 1200
B. TỰ LUẬN (7,0 điểm)
Bài 1. (1,5 điểm)
a) Vẽ đồ thị (P) của hàm số
2
1
4
= −yx
b) Tìm các điểm thuộc (P) có hoành độ và tung độ là hai số đối nhau.
Bài 2. (0,5 điểm) Giải phương trình sau :
( )
22
21 3 6xx+= +
Bài 3. ( 1,0 điểm) Theo kế hoạch , Công an tỉnh Khánh Hòa sẽ cấp 7200 thẻ căn cước công dân cho
địa phương A. Một tổ công tác được điều động đến địa phương A để cấp thẻ căn cước công
dân trong một thời gian nhất định.Khi thực hiện nhiệm vụ, tổ chức công tác đã cải tiến kĩ
thuật nên mỗi ngày đã cấp tăng thêm được 40 thẻ Căn cước so với kế hoạch . Vì vậy , tổ công
tác đã hoàn thành nhiệm vụ sớm hơn kế hoạch 2 ngày. Hỏi theo kế hoạch ban đầu, mỗi ngày
tổ công tác sẽ cung cấp được bao nhiêu thẻ Căn cước công dân?
Bài 4. (1,5 điểm) Cho phương trình:
+ −=
2
3 2 30xx
.
a) Chứng minh phương trình trên có hai nghiệm phân biệt.
b) Không giải phương trình, tính giá trị của biểu thức:
( )( )
=− −+
2
1 221 2
2M x xxx x
.
Bài 5. (2,5 điểm) Cho
ABC∆
nhọn (AB < AC) nội tiếp đường tròn (O; R) . Ba đường cao AD,
BE và CF cắt nhau tại H.
a) (1,0 điểm) Chứng minh: tứ giác BFEC nội tiếp.
b) (0,5 điểm) Kẻ đường kính AK của (O). Chứng minh: AD.AK = AB.AC.
c) (1,0 điểm) Gọi M là trung điểm của BC. Giả sử
0
60BAC =
. Chứng minh H, M, K thẳng
hàng và tính bán kính đường tròn ngoại tiếp ∆HEF theo R.
-----HẾT-----
UBND QUẬN BÌNH THẠNH
TRƯỜNG THCS ĐỐNG ĐA
ĐÁP ÁN ĐỀ KIỂM TRA GIỮA KỲ II NĂM HỌC 2024 - 2025
MÔN TOÁN LỚP 9
A. PHẦN TRẮC NGHIỆM: (3,0 điểm) Mỗi câu đúng 0,25 điểm
Câu
1
2
3
4
5
6
7
8
9
10
11
12
A X X X
B X X X X
C X X
D X X X
B. PHẦN TỰ LUẬN: (7,0 điểm)
Câu Nội dung Điểm
1
Bài 1. (1,5 điểm)
a) Vẽ đồ thị (P) của hàm số
2
1
4
= −yx
+ Lập BGT
+ Vẽ đồ thị
0,5
0,5
b) Tìm các điểm thuộc (P) có hoành độ và tung độ là hai số đối nhau.
+ Điểm cần tìm có hoành độ và tung độ là hai số đối nhau nên
0xy x y+=⇒=−
+ Thay
xy= −
vào hàm số
2
1
4
= −yx
ta có
2
2
2
1()
4
1
4
10
4
=−−
= −
+=
yy
yy
yy
0y=
hoặc
4y= −
+ Với
00y xy= ⇒ =−=
+ Với
44y xy=−⇒ =−=
Vậy các điểm cần tìm là
(0;0)
và
(4; 4)−
0,25
0,25
2
Bài 2. (0,5 điểm) Giải phương trình sau :
( )
22
21 3 6xx+= +
2
4 50xx+ −=
Ta có
1450abc++=++=
Vậy phương trình có 2 nghiệm:
1
1x=
2
55
1
c
xa
−
= = = −
0,25
0,25
3
Bài 3. ( 1,0 điểm)
Câu Nội dung Điểm
Gọi số thẻ Căn cước mỗi ngày tổ công tác cấp được theo kế hoạch là (
xN
∗
∈
)
Theo kế hoạch, tổ công tác sẽ hoàn thành nhiệm vụ trong
7200
x
ngày
Sau khi cải tiến kĩ thuật, mỗi ngày tổ công tác cấp được
40x+
thẻ.
Sau khi cải tiến kĩ thuật , tổ công tác hoàn thành nhiệm vụ trong
7200
40x+
ngày
Khi thực hiện nhiệm vụ, tổ công tác đã cải tiến kĩ thuật nên mỗi ngày đã cấp tăng
thêm 40 thẻ Căn cước so với kế hoạch. Vì vậy, tổ công tác đã hoàn thành nhiệm
vụ sớm hơn kế hoạch 2 ngày nên ta có phương trình:
7200 7200 2
40xx
−=
+
2
2 80 288000 0xx+− =
360=x
(nhận) hoặc
400= −x
(loại)
Vậy theo kế hoạch ban đầu, mỗi ngày tổ công tác cấp được 360 thẻ căn cước
0,25
0,25
0,25
025
4
Bài 4. (1,5 điểm) Cho phương trình:
+ −=
2
3 2 30xx
.
a) Chứng minh phương trình trên có hai nghiệm phân biệt.
Ta có
= >30a
và
=−<30c
. Vì a và c trái dấu
Nên phương trình có hai nghiệm phân biệt
12
,xx
.
0,25
0,25
b) Không giải phương trình, tính giá trị của biểu thức:
( )( )
=− −+
2
1 221 2
2M x xxx x
.
Vì phương trình trên có hai nghiệm phân biệt
12
,xx
Theo định lí Vi-et, ta có:
−−
+= =
= = −
12
12
2
3
.1
b
xx
a
c
xx
a
Ta có:
( )( )
=− −+
2
1 221 2
2M x xxx x
( )
( )
( )
( )
= −− + +
= −+

= −+−


= −+

−−
= −− =


22 2
12 1 2 12 2
22
12 1 2
2
12 1 2 12
2
12 1 2
2
22
3
32
5
2 49
5. 1 39
M xx x x xx x
M xx x x
M xx x x xx
M xx x x
M
0,25
0,25
0,25
0,25
5
Bài 5. (2,5 điểm) Cho
ABC∆
nhọn (AB < AC) nội tiếp đường tròn (O; R) . Ba
đường cao AD, BE và CF cắt nhau tại H.
a) (1 điểm) Chứng minh: tứ giác BFEC nội tiếp.
b) (0,5 điểm) Kẻ đường kính AK của (O). Chứng minh: AD.AK = AB.AC.
c) (1,0 điểm) Gọi M là trung điểm của BC. Giả sử
0
60BAC =
. Chứng minh H, M,
K thẳng hàng và tính bán kính đường tròn ngoại tiếp ∆HEF theo R.